Unit 4 Acid-Base and Solubility Equilibria
4.2 pH Calculations and Acid-Base Strength
OpenStax
Section Learning Objectives
- Explain the characterization of aqueous solutions as acidic, basic, or neutral.
- Express hydronium and hydroxide ion concentrations on the pH and pOH scales.
- Perform calculations relating pH and pOH.
- Assess the relative strengths of acids and bases according to their ionization constants.
- Carry out equilibrium calculations for weak acid–base systems.
✓ SECTION 4.2 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion. | No | 90 min |
| Optional Resource: Watch a video explanation about the pH scale and acid strength. | No | 6 min |
| Optional Activity: View a simulation on strong and weak acids and bases. | No | 15 min |
| Optional Activity: Explore the simulation on how pH and percent ionization varies with the dilution of an acid. | No | 15 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 30 min |
📖 READING PORTION
Definitions of Neutral, Acidic, and Basic Solutions
As discussed in Section 4.1, hydronium and hydroxide ions are present both in pure water and in all aqueous solutions, and their concentrations are inversely proportional as determined by the ion product of water (Kw). The concentrations of these ions in a solution are often critical determinants of the solution’s properties and the chemical behaviours of its other solutes, and specific vocabulary has been developed to describe these concentrations in relative terms. A solution is neutral if it contains equal concentrations of hydronium and hydroxide ions; acidic if it contains a greater concentration of hydronium ions than hydroxide ions; and basic (alkaline) if it contains a lesser concentration of hydronium ions than hydroxide ions.
pH and pOH
A common means of expressing quantities that may span many orders of magnitude is to use a logarithmic scale. One such scale that is very popular for chemical concentrations and equilibrium constants is based on the p-function, where the “p” stands for the negative of the base-10 logarithm. The pH of a solution is therefore defined as shown here, where [H3O+] is the molar concentration of hydronium ion in the solution
Equation 1
[latex]\text{pH} = −\log[\text{H}_3\text{O}^+][/latex]
Exponentiating the equation to isolate the hydronium ion molarity yields the equivalent expression
Equation 2
[latex][\text{H}_3\text{O}^+] = 10^{−\text{pH}}[/latex]
Likewise, the hydroxide ion molarity may be expressed as the pOH
Equation 3
[latex]\text{pOH} = −\log[\text{OH}^−][/latex]
or
Equation 4
[latex][\text{OH}^−] = 10^{−\text{pOH}}[/latex]
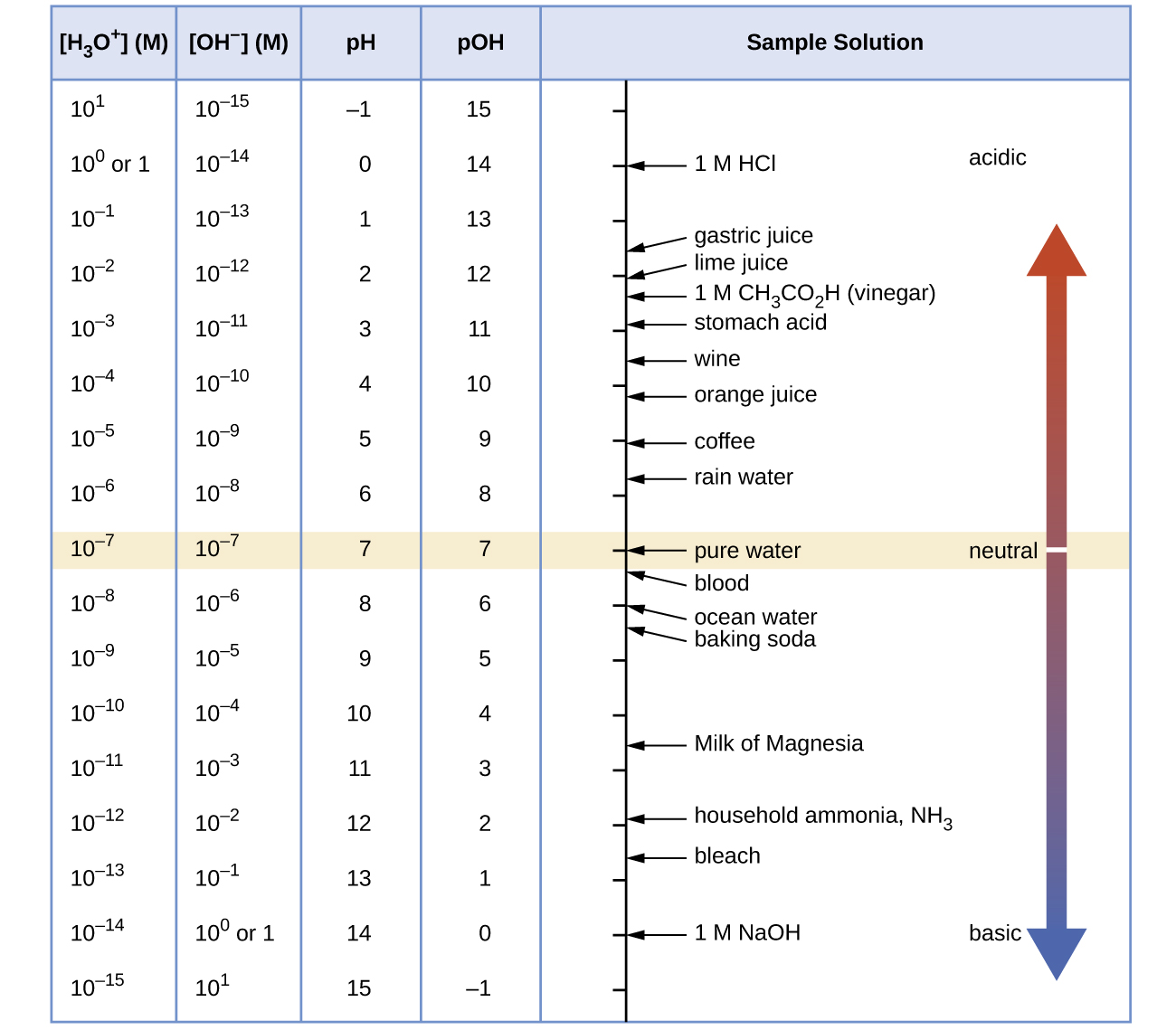
![]()
The significant digit rule for pH and pOH is rather peculiar because pH and pOH are logarithms. When using [H3O+] to calculate pH, the number of significant digits in [H3O+] corresponds to the number of decimal places in pH. For example, [H3O+] = 2.53 × 10-5 M (three significant digits) gives pH = −log(2.53 × 10−5) = 4.597 (three decimal places). Conversely, the number of decimal places in pH indicates the number of significant digits in [H3O+]. Likewise, the number of decimal places in pOH is the number of significant digits in the corresponding [OH−].
As was shown in Section 4.1, the hydronium ion molarity in pure water (or any neutral solution) is 1.0 × 10−7 M at 25 °C. The pH and pOH of a neutral solution at this temperature are therefore
[latex]\text{pH} = −\log[\text{H}_3\text{O}^+] =−\log(1.0×10^{−7})=\boxed{7.00}[/latex]
[latex]\text{pOH} = −\log[\text{OH}^−] =−\log(1.0×10^{−7})=\boxed{7.00}[/latex]
And so, at this temperature, acidic solutions are those with hydronium ion molarities greater than 1.0 × 10−7 M and hydroxide ion molarities less than 1.0 × 10−7 M (corresponding to pH values less than 7.00 and pOH values greater than 7.00). Basic solutions are those with hydronium ion molarities less than 1.0 × 10−7 M and hydroxide ion molarities greater than 1.0 × 10−7 M (corresponding to pH values greater than 7.00 and pOH values less than 7.00).
Finally, the relation between hydronium and hydroxide concentrations is derived from the Kw expression as pKw
[latex]K_{\text{w}} = [\text{H}_3\text{O}^+][\text{OH}^−][/latex]
[latex]−\log K_{\text{w}} = −\log([\text{H}_3\text{O}^+][\text{OH}^−]) = −\log[\text{H}_3\text{O}^+] + −\log[\text{OH}^−][/latex]
[latex]\text{p}K_{\text{w}} = \text{pH} + \text{pOH}[/latex]
At 25°C, the value of Kw is 1.0 × 10−14. For CHEM 1523, the acid-base questions we cover will be at 25°C unless otherwise specified. The pKw equation is thus equal to the constant 14.00
Equation 5
[latex]\text{p}K_{\text{w}} = 14.00 = \text{pH} + \text{pOH}[/latex]
Since the autoionization constant Kw is temperature dependent, these correlations between pH values and the acidic/neutral/basic adjectives will be different at temperatures other than 25 °C. For example, the hydronium molarity of pure water at 80 °C is 4.9 × 10−7 M, which corresponds to pH and pOH values of
[latex]\text{pH} = −\log[\text{H}_3\text{O}^+] =−\log(4.9×10^{−7})=6.31[/latex]
[latex]\text{pOH} = −\log[\text{OH}^−] =−\log(4.9×10^{−7})=6.31[/latex]
At this temperature, then, neutral solutions exhibit pH = pOH = 6.31, acidic solutions exhibit pH less than 6.31 and pOH greater than 6.31, whereas basic solutions exhibit pH greater than 6.31 and pOH less than 6.31. This distinction can be important when studying certain processes that occur at other temperatures, such as enzymatic reactions in warm-blooded organisms at a temperature around 36–40 °C. Unless otherwise noted, references to pH values are presumed to be those at 25 °C (Table 1). Figure 1 shows the relationships between [H3O+], [OH−], pH, and pOH for solutions classified as acidic, basic, and neutral.
|
Classification |
Relative Ion Concentrations |
pH at 25 °C |
|
Acidic |
[H3O+] > [OH−] |
pH < 7 |
|
Neutral |
[H3O+] = [OH−] |
pH < 7 |
|
Basic |
[H3O+] < [OH−] |
pH > 7 |
|
Table 1 Summary of Relations for Acidic, Basic and Neutral Solutions. Source: OpenStax Chemistry |
||
Example 1
Calculation of pH from [H3O+]
What is the pH of stomach acid, a solution of HCl with a hydronium ion concentration of 1.2 × 10−3 M?
SOLUTION
[latex]\text{pH} = −\log[\text{H}_3\text{O}^+] = −\log(1.2×10^{−3}) = −(−2.92) = \boxed{2.92}[/latex]
Example 2
Calculation of Hydronium Ion Concentration from pH
Calculate the hydronium ion concentration of blood, the pH of which is 7.3.
SOLUTION
[latex]\text{pH} = −\log[\text{H}_3\text{O}^+] = 7.3[/latex]
[latex]\log[\text{H}_3\text{O}^+] = −7.3[/latex]
[latex][\text{H}_3\text{O}^+] = 10^{−7.3}[/latex] or [latex][\text{H}_3\text{O}^+] = \text{ antilog of } −7.3[/latex]
[latex][\text{H}_3\text{O}^+] = \boxed{5×10^{−8} \text{ M}}[/latex]
Example 3
Calculation of pOH
What are the pOH and the pH of a 0.0125-M solution of potassium hydroxide, KOH?
SOLUTION
Potassium hydroxide is a highly soluble ionic compound and completely dissociates when dissolved in dilute solution, yielding [OH−] = 0.0125 M.
[latex]\text{pOH} = −\log[\text{OH}^−] = −\log(0.0125) = −(−1.903) = \boxed{1.903}[/latex]
The pH can be found from the pOH.
pH + pOH = 14.00
pH = 14.00 – pOH = 14.00 – 1.903 = [latex]\boxed{12.10}[/latex]
Acid and Base Ionization Constants
The relative strength of an acid or base is the extent to which it ionizes when dissolved in water. If the ionization reaction is essentially complete, the acid or base is termed strong; if relatively little ionization occurs, the acid or base is weak. As will be evident throughout the remainder of this chapter, there are many more weak acids and bases than strong ones. The most common strong acids and bases are listed in Table 2.
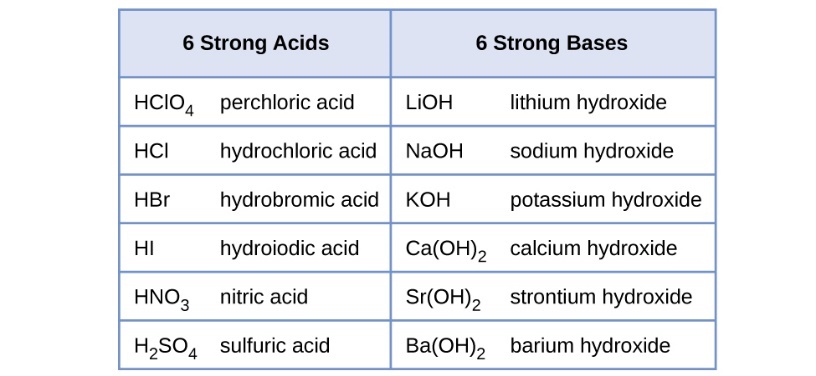
Table 2 Some of the common strong acids and bases are listed here. Source: OpenStax Chemistry 2e
The relative strengths of acids may be quantified by measuring their equilibrium constants in aqueous solutions. In solutions of the same concentration, stronger acids ionize to a greater extent, and so yield higher concentrations of hydronium ions than do weaker acids. The equilibrium constant for an acid is called the acid-ionization constant, Ka. For the reaction of an acid HA,
HA(aq) + H2O(l) ⇌ H3O+(aq) + A−(aq),
the acid ionization constant is written as
Equation 6
[latex]K_{\text{a}}=\frac{[\text{H}_3\text{O}^+][\text{A}^−]}{[\text{HA}]}[/latex]
where the concentrations are those at equilibrium. Although water is a reactant in the reaction, it is the solvent as well, so we do not include [H2O] in the equation. The larger the Ka of an acid, the larger the concentration of H3O+ and A− relative to the concentration of the nonionized acid, HA, in an equilibrium mixture, and the stronger the acid. An acid is classified as “strong” when it undergoes complete ionization, in which case the concentration of the nonionized acid (HA) approaches zero and the acid ionization constant (Ka) is much greater than 1. Acids that are partially ionized are called “weak,” and their acid ionization constants may be experimentally measured.
To illustrate this idea, three acid ionization equations and Ka values are shown below. The ionization constants increase from first to last of the listed equations, indicating the relative acid strength increases in the order CH3COOH < HNO2 < HSO4−:
[latex]\begin{eqnarray} \text{CH}_3\text{COOH}(aq)+\text{H}_2\text{O}(l) &\rightleftharpoons& \text{H}_3\text{O}^+(aq)+\text{CH}_3\text{COO}^-(aq) &K_{\text{a}}=1.8\times 10^{-5} \\ \text{HNO}_2(aq)+\text{H}_2\text{O}(l) &\rightleftharpoons& \text{H}_3\text{O}^+(aq)+\text{NO}_2^-(aq) &K_{\text{a}}=4.6\times 10^{-4} \\ \text{HSO}_4^-(aq)+\text{H}_2\text{O}(l) &\rightleftharpoons& \text{H}_3\text{O}^+(aq)+\text{SO}_4^{2-}(aq) &K_{\text{a}}=1.2\times 10^{-2} \end{eqnarray}[/latex]
Another measure of the strength of an acid is its percent ionization. The percent ionization of a weak acid is defined in terms of the composition of an equilibrium mixture
Equation 7
[latex]\text{% ionization}=\frac{[\text{H}_3\text{O}^+]_{\text{eq}}}{[\text{HA}]_\text{initial}}×100\%[/latex]
where the numerator is equivalent to the concentration of the acid’s conjugate base (per stoichiometry, [A−] = [H3O+]). Unlike the Ka value, the percent ionization of a weak acid varies with the initial concentration of acid, typically decreasing as concentration increases. Equilibrium calculations of the sort can be used to confirm this behaviour.
Just as for acids, the relative strength of a base is reflected in the magnitude of its base-ionization constant (Kb) in aqueous solutions. The stronger the base, the larger the Kb. In solutions of the same concentration, stronger bases ionize to a greater extent, and so yield higher hydroxide ion concentrations than do weaker bases. A stronger base has a larger ionization constant than does a weaker base. For the reaction of a base B,
B(aq) + H2O(l) ⇌ HB+(aq) + OH−(aq),
the ionization constant is written as
Equation 8
[latex]K_{\text{b}}=\frac{[\text{HB}^+][\text{OH}^−]}{[\text{B}]}[/latex]
Inspection of the data for three weak bases presented below shows the base strength increases in the order NO2− < CH3COO− < NH3:
[latex]\begin{eqnarray} \text{NO}_2(aq)^-+\text{H}_2\text{O}(l) &\rightleftharpoons& \text{HNO}_2(aq)+ \text{OH}^−(aq) &K_{\text{b}}=2.17\times 10^{-11} \\ \text{CH}_3\text{COO}^-(aq)+\text{H}_2\text{O}(l) &\rightleftharpoons& \text{CH}_3\text{COOH}(aq)+ \text{OH}^−(aq) &K_{\text{b}}=5.6\times 10^{-10} \\ \text{NH}_3 (aq)+\text{H}_2\text{O}(l) &\rightleftharpoons& \text{NH}_4^{+}(aq)+ \text{OH}^−(aq) &K_{\text{b}}=1.8\times 10^{-5} \end{eqnarray}[/latex]
Relative Strengths of Conjugate Acid-Base Pairs
Brønsted-Lowry acid-base chemistry is the transfer of protons; thus, logic suggests a relation between the relative strengths of conjugate acid-base pairs. The strength of an acid or base is quantified in its ionization constant, Ka or Kb, which represents the extent of the acid or base ionization reaction. For the conjugate acid-base pair HA/A−, ionization equilibrium equations and ionization constant expressions are
HA(aq) + H2O(l) ⇌ H3O+(aq) + A−(aq) [latex]\;\;\;[/latex] [latex]K_{\text{a}}=\frac{[\text{H}_3\text{O}^+][\text{A}^−]}{[\text{HA}]}[/latex]
A−(aq) + H2O(l) ⇌ OH−(aq) + HA(aq) [latex]\;\;\;[/latex] [latex]K_{\text{b}}=\frac{[ \text{OH}^−] [\text{HA}]}{[\text{A}^−]}[/latex]
Adding these two chemical equations yields the equation for the autoionization for water
HA(aq) + H2O(l) + A−(aq) + H2O(l) ⇌ H3O+(aq) + A−(aq) + OH−(aq) + HA(aq)
2 H2O(l) ⇌ H3O+(aq) + OH−(aq)
The equilibrium constant for a summed reaction is equal to the mathematical product of the equilibrium constants for the added reactions, and so
[latex]K_{\text{a}}×K_{\text{b}}=\frac{[\text{H}_3\text{O}^+][\text{A}^−]}{[\text{HA}]}×\frac{[\text{HA}][\text{OH}^−]}{[\text{A}^−]}=[\text{H}_3\text{O}^+][\text{OH}^−][/latex]
Equation 9
[latex]K_{\text{a}}×K_{\text{b}}=K_{\text{w}}[/latex] (= 1.0 × 10−14 at 25 °C)
This equation states the relation between ionization constants for any conjugate acid-base pair, namely, their mathematical product is equal to the ion product of water, Kw. By rearranging this equation, a reciprocal relation between the strengths of a conjugate acid-base pair becomes evident
Equation 10
[latex]K_{\text{a}}=\frac{K_{\text{w}}}{K_{\text{b, conj base}}}[/latex] or [latex]K_{\text{b}}=\frac{K_{\text{w}}}{K_{\text{a, conj acid}}}[/latex], where [latex]K_{\text{w}}=1.0×10^{−14}[/latex] at 25 °C
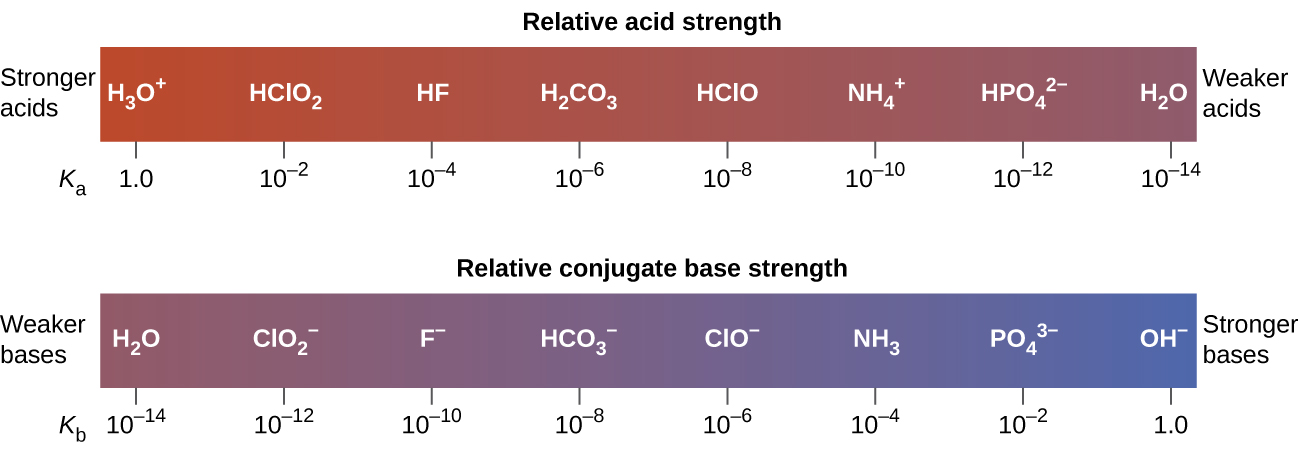
The inverse proportional relation between Ka and Kb means the stronger the acid or base, the weaker its conjugate partner. Figure 2 illustrates this relation for several conjugate acid-base pairs.
Example 4
Calculating Ionization Constants for Conjugate Acid-Base Pairs
Use the Kb for the nitrite ion, NO2−, to calculate the Ka for its conjugate acid.
SOLUTION
Kb for NO2− is given as 2.17 × 10−11. The conjugate acid of NO2− is HNO2; Ka for HNO2 can be calculated using the relationship (Equation 10):
[latex]K_{\text{a}}×K_{\text{b}}=K_{\text{w}}=1.0×10^{−14}[/latex]
Solving for Ka yields
[latex]K_{\text{a}}=\frac{K_{\text{w}}}{K_{\text{b}}}=\frac{1.0×10^{−14}}{2.17×10^{−11}}=4.6×10^{−4}[/latex]
Acid-Base Equilibrium Calculations
Section 3.4 on chemical equilibria introduced several types of equilibrium calculations and the various mathematical strategies that are helpful in performing them. These strategies are generally useful for equilibrium systems regardless of chemical reaction class, and so they may be effectively applied to acid-base equilibrium problems. Here are several example exercises involving equilibrium calculations for acid-base systems.
Example 5
Determination of Ka from Equilibrium Concentrations
Acetic acid is the principal ingredient in vinegar that provides its sour taste. At equilibrium, a solution contains [CH3COOH] = 0.0787 M and [H3O+] = [CH3COO−] = 0.00118 M. What is the value of Ka for acetic acid?
SOLUTION
The relevant equilibrium equation and its equilibrium constant expression are shown below. Substitution of the provided equilibrium concentrations permits a straightforward calculation of the Ka for acetic acid.
CH3COOH(aq) + H2O(l) ⇌ H3O+(aq) + CH3COO−(aq)
[latex]K_{\text{a}}=\frac{{[\text{H}_3\text{O}^+][\text{CH}_3\text{COO}^−]}}{{[\text{CH}_3\text{COOH}]}}=\frac{(0.00118)(0.00118)}{0.0787}=\boxed{1.77×10^{−5}}[/latex]
Example 6
Calculating Equilibrium Concentrations in a Weak Acid Solution
Formic acid, HCOOH, is one irritant that causes the body’s reaction to some ant bites and stings.
What is the concentration of hydronium ion and the pH of a 0.534-M solution of formic acid?
HCOOH(aq) + H2O(l) ⇌ H3O+(aq) + HCOO−(aq) [latex]\;\;\;[/latex] Ka = 1.8 × 10−4
SOLUTION
The ICE table for this system is
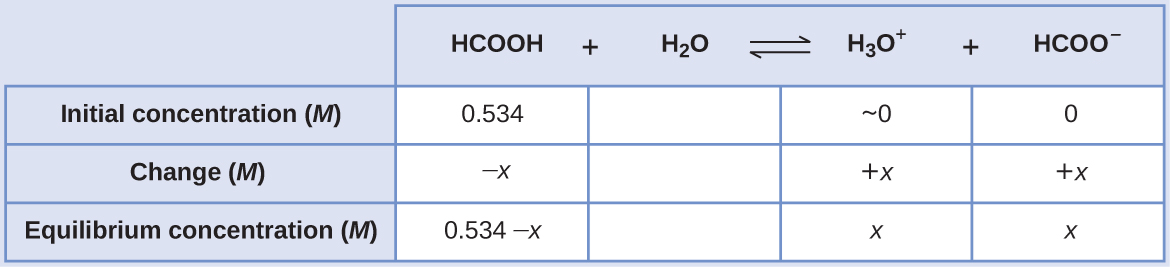
Substituting the equilibrium concentration terms into the Ka expression gives
[latex]\begin{array}{l l} K_{\text{a}}=1.8×10^{−4}&=\frac{[\text{H}_3\text{O}^+][\text{HCOO}^−]}{[\text{HCOOH}]} \\ &=\frac{x\cdot x}{0.534−x} \end{array}[/latex]
The relatively large initial concentration and small equilibrium constant permits the simplifying assumption that x will be much lesser than 0.534, and so the equation becomes
[latex]K_{\text{a}}=1.8×10^{−4}\approx \frac{x^2}{0.534}[/latex]
Solving the equation for x yields
[latex]x^2=0.534×(1.8×10^{−4})=9.6×10^{−5}[/latex]
[latex]x=\sqrt{9.6×10^{−5}}=\boxed{9.8×10^{−3} \text{ M}}[/latex]
To check the assumption that x is small compared to 0.534, its relative magnitude can be estimated:
[latex]\frac{x}{0.534}=\frac{9.8×10^{−3}}{0.534}=1.8×10^{−2}[/latex] which is 1.8% of 0.534
Because x is less than 5% of the initial concentration, the assumption is valid.
As defined in the ICE table, x is equal to the equilibrium concentration of hydronium ion:
x = [H3O+] = 0.0098 M
Finally, the pH is calculated to be
pH = −log[H3O+] = −log(0.0098) = [latex]\boxed{2.01}[/latex]
Example 7
Calculating Equilibrium Concentrations in a Weak Base Solution
Calculate the pH of an aqueous solution containing 1.00 g of NaClO in 500 mL (= 0.500 L) of water, where HClO has Ka = 2.9 × 10−8. Note that NaClO is an ionic compound that dissociates into Na+ and ClO−.
SOLUTION
The sodium ion is neutral in water, but ClO− is basic. We can calculate the moles and concentration of ClO−
[latex]\text{NaClO}(s)\; \overset{\text{H}_2\text{O}}{\longrightarrow}\;\text{Na}^+(aq)\;+\;\text{ClO}^-(aq)[/latex]
[latex]\begin{align*} n_{\text{ClO}^-} &= (1.00 \text{ g NaClO})\left(\dfrac{1 \text{ mol NaClO}}{74.44\text{ g NaClO}}\right)\left(\dfrac{1 \text{ mol ClO}^-}{1 \text{ mol NaClO}}\right) = 0.0134 \text{ mol ClO}^- \\ \\ [\text{ClO}^-] &= \dfrac{0.0134 \text{ mol ClO}^-}{0.500 \text{ L}} = 0.0269 \text{ M ClO}^- \end{align*}[/latex]
The ICE table for this system is
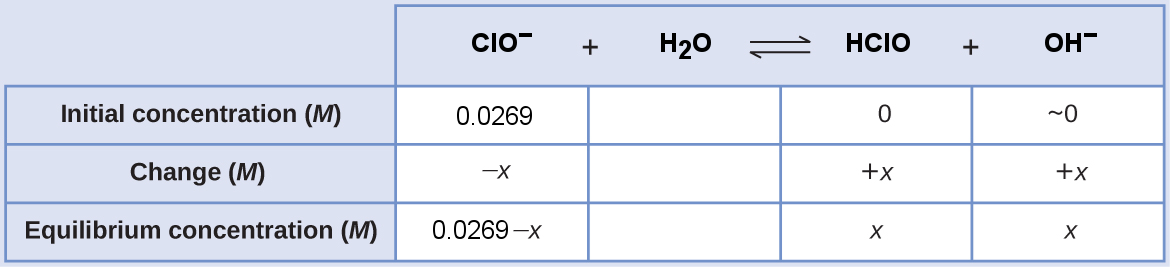
Substitute the equilibrium concentration terms into the Kb expression. The Kb of ClO− comes from dividing Kw by the Ka of HClO, [latex]K_{\text{b}} = \frac{1.0\times 10^{-14}}{2.9 \times 10^{-8}}[/latex]
[latex]\begin{align} K_{\text{b}}&=\dfrac{[\text{HClO}][\text{OH}^−]}{[\text{ClO}^-]} \\ \dfrac{1.0\times 10^{-14}}{2.9 \times 10^{-8}} &= \dfrac{x \cdot x}{0.0269 - x} \end{align}[/latex]
The relatively large initial concentration and small equilibrium constant permits the simplifying assumption that x will be much lesser than 0.0269, and so the equation becomes
[latex]K_{\text{b}} = \dfrac{1.0\times 10^{-14}}{2.9 \times 10^{-8}} \approx \dfrac{x^2}{0.0269}[/latex]
Solving the equation for x yields
[latex]\begin{align} x^2&=\left(\dfrac{1.0\times 10^{-14}}{2.9 \times 10^{-8}}\right)(0.0269)=9.3×10^{−9} \\ \\x&=\sqrt{9.3\times10^{−9}}=9.6×10^{−5} \text{ M} \end{align}[/latex]
To check the assumption that x is small compared to 0.0269, its relative magnitude can be estimated
[latex]\begin{align} \text{% ionization}&=\dfrac{[\text{OH}^-]_{\text{eq}}}{[\text{ClO}^-]_\text{initial}}\times 100\% \\ \\ &=\dfrac{9.6\times10^{-5}\text{ M}}{0.0269 \text{ M}} \times 100\% \\ \\ &=0.36\% \end{align}[/latex]
Because x is less than 5% of the initial concentration, the assumption is valid.
As defined in the ICE table, x is equal to the equilibrium concentration of hydroxide ion, from which we can calculate pOH and pH
\begin{align} [\text{OH}^-]&=9.6 \times10^{-5} \text{ M} \\ \text{pOH} &= -\log(9.6 \times10^{-5}) = 4.02 \\ \text{pH} &= 14.00 – \text{pOH} = 14.00 – 4.02 = \boxed{9.98}
\end{align}
Optional Resource
Watch this video explanation about the pH scale and acid strength.
Video 1 GCSE Chemistry – The pH Scale & Strong vs Weak Acids (5 min 11 s).
Optional Activities
♦ View the simulation of strong and weak acids and bases at the molecular level.
♦ Use this simulation to see how pH and percent ionization varies by how much an acid is diluted. Select from 1.0, 0.10, and 0.010 M solutions. The pH of acids increases as hydronium ion concentration is diluted, but the percent ionization of weak acids increases with dilution.
What is the pH of a 0.020 mol/L solution of Ba(OH)2 at 25°C?
Click to see answer
[latex]\text{Ba(OH)}_2(s) \longrightarrow \text{Ba}^{2+}(aq)+2 \text{ OH}^-(aq)[/latex]
[latex][\text{OH}^-]=\left(\dfrac{0.020 \text{ mol Ba(OH)}_2}{\text{L}}\right)\left(\dfrac{2 \text{ mol OH}^-}{1 \text{ mol Ba(OH)}_2}\right)=0.040 \text{ mol/L OH}^-[/latex]
[latex]\begin{eqnarray} K_\text{w}&=&[\text{H}_3\text{O}^+][\text{OH}^-] \\ \Leftrightarrow [\text{H}_3\text{O}^+]&=& \dfrac{K_{\text{w}}}{[\text{OH}^-]} \\ &=&\dfrac{1.0 \times 10^{-14}}{0.040} \\ &=& 2.5 \times 10^{-13} \text{ M} \end{eqnarray}[/latex]
[latex]\text{pH}=-\log[\text{H}_3\text{O}^+]=-\log(2.5 \times 10^{-13})=\boxed{12.60}[/latex]

