Unit 1 Gases
1.3 The Kinetic-Molecular Theory of Gases
OpenStax
Section Learning Objectives
- Discuss the postulates of the kinetic-molecular theory of gases.
- Explain the distribution of molecular speeds in a sample of a gas and how that changes with temperature.
- Calculate the root-mean-square speed of a gas.
✓ SECTION 1.3 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion and videos. | No | 60 min |
| Optional Resource: Watch a video explanation about the kinetic-molecular theory. | No | 7 min |
| Optional Activity: Explore the simulation on the kinetic energy and speed distributions of gases. | No | 10 min |
| Work on the self-check question. | No | 5 min |
| Work on practice exercises. | No | 65 min |
📖 READING PORTION
The Behaviour of Gas Particles at the Microscopic Level
The simple gas laws and the ideal gas law were based on empirical observations at the macroscopic level and do not explain why gases follow these relationships. The kinetic-molecular theory of gases is seen as an elegant and useful model for explaining the behaviour of gases, and the model explains the origin of the simple gas laws and ideal gas law by treating particles as nothing more than colliding balls (or points) bouncing around randomly through a room in a straight line until they collide with a wall or another particle. When we assume these collisions occur elastically (as we do in the ideal gas model) then the two colliding particles together must have the same total energy before and after the collision, but each particle may now have a different share of energy as it speeds off in a new direction. This gives rise to the constant random motion we also expect from an ideal gas. In many ways the kinetic-molecular theory is a refinement of our understanding of the ideal gas model.
The kinetic-molecular theory gives a framework to explain the gas laws at the microscopic level. The postulates of the kinetic-molecular theory are:
- A gas is made up of an extremely large number of very small particles (molecules or atoms) moving in constant, random, straight-line motion. Here, we have the same basis as the ideal gas model, but now we acknowledge that we know particles have size, but there are a whole lot of very small particles in a gas.
- The distance between any two gas particles is vast in comparison to the size of the particles meaning that most of the space is empty and the particles can be treated as point masses (no volume). Here we get back the best assumption of the ideal gas law. Since the volume of space is so vast in comparison to the volume of a particle, we can treat the particle as if it has no relative volume.
- Gas particles do not exert attractive or repulsive forces with each other or with the container walls. Particles collide elastically with each other and the container walls. This means that colliding particles do not lose energy.
- The pressure exerted by a gas is caused by collisions between gas particles with the container wall. This is the definition of pressure at the microscopic level.
- The absolute (measured in kelvin) temperature is proportional to the average kinetic energy of gas particles. This is the definition of temperature at the microscopic level. At a higher temperature, gas particles move more quickly and thus have more kinetic energy than at lower temperature.
Consider how the kinetic-molecular theory applies to Boyle’s Law. For a fixed amount of gas at a fixed temperature, the pressure and volume are inversely proportional. As volume decreases, the gas particles will be exposed to a smaller surface area within the container. Pressure will increase because the frequency of collisions with the container wall will increase. Conversely, as volume increases, gas particles will travel a farther distance before encountering the container wall. Pressure will decrease as collisions with the container wall will become less frequent.
Charles’ Law, in terms of kinetic-molecular theory, is about what happens when we increase the total kinetic energy of a gas by increasing its temperature. If we heat the gas in a rigid container, we would see the pressure of the gas inside increase with an increase in temperature, because the particles are moving faster and causing more frequent collisions with the container wall. Pressure can be kept constant when the volume of the container is allowed to increase. The frequency of collisions with the container wall decreases because particles travel greater distances before reaching the container wall.
Finally, Avogadro’s Law is really very similar to Charles’ Law from a kinetic-molecular theory standpoint, and explains why these two laws show the same mathematical behaviour. If we pump more gas into a rigid container at a fixed temperature, the increased number of particles translate to increased number of collisions with the container wall. To keep the pressure constant, the volume of the container can expand to accommodate the increase in gas particles.
Kinetic Energy and Speed of Gas Particles
Another aspect of the kinetic-molecular theory is that we can connect the total kinetic energy of a gas sample to a distribution of the speeds and kinetic energies of the individual particles themselves. Since temperature is an indicator of the average kinetic energy of particles, then the temperature is connected to the distribution of molecular kinetic energies (Figure 1). As such, when the temperature is increased, we would expect, on average, that particles will move faster and have more kinetic energy as a result. However, when we consider how this affects an ideal gas, an interesting point comes out of this.
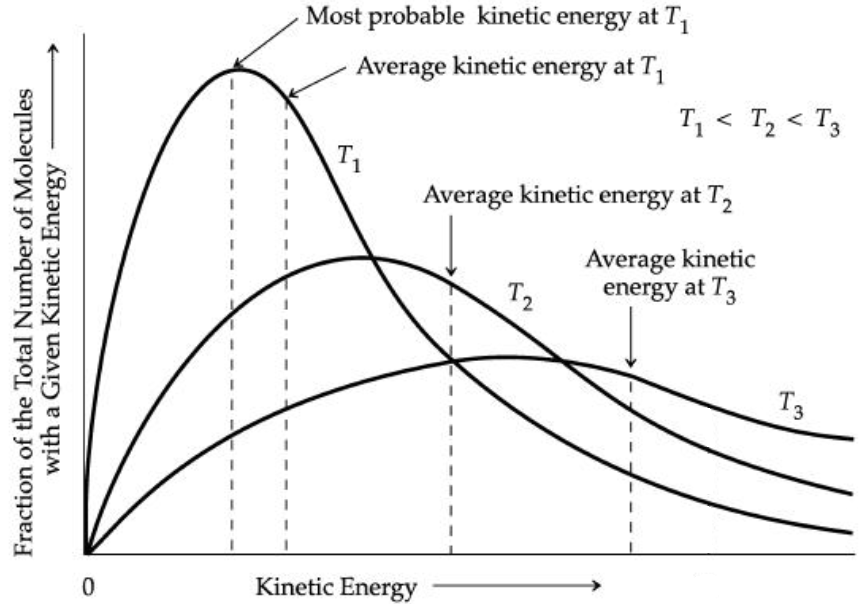
If temperature and amount of gas solely determines the total kinetic energy density of an ideal gas, then the nature of the gas is irrelevant. So, when we look at one mole of two different gases at the same temperature and pressure, those two gas samples have the exact same total kinetic energy. The kinetic energy of a particle of mass m and speed v is
EK = ½ mv2
Notice that for kinetic energy to remain constant, increases in mass will be offset by decreases in speed and vice versa. If one of the gases has particles with more mass than the other gas, the heavier gas particles will have to move more slowly so their heftier bulks contain the same kinetic energy as their lighter cousins in the other sample. Simply put, heavier particles move more slowly than lighter particles at a given temperature. This concept is applied in Graham’s Law of Diffusion and Effusion in Section 1.4.
The average kinetic energy for the entire sample of gas particles is
Equation 1
[latex]E_{\text{K, ave}} = (3/2)RT/N_{\text{A}}[/latex]
- [latex]E_{\text{K, ave}}[/latex], average kinetic energy ([latex]\text{J}[/latex])
- [latex]R[/latex], gas constant ([latex]8.314\frac{\text{J}}{\text{mol}\cdot\text{K}}[/latex])
- [latex]T[/latex], kelvin or absolute temperature
- [latex]N_{\text{A}}[/latex], Avogadro’s number ([latex]6.022 \times 10^{23}/\text{mol}[/latex])
The amount of kinetic energy that most particles (most probable) have is not equal to the average kinetic energy of all the particles because the Maxwell-Boltzmann distribution is not a symmetric distribution.
Although Figure 1 plots kinetic energy on the horizontal axis, the shape of the distribution is similar if the horizontal axis was the speed of particles. The reason is that kinetic energy parallels speed. The average speed of a particle in the distribution of speeds can be defined several different ways because of the asymmetric distribution. One measure of average speed is the root-mean-square speed, urms,
Equation 2
- [latex]u_{\text{rms}}[/latex], root-mean-square speed ([latex]\text{m/s}[/latex])
- [latex]R[/latex], gas constant ([latex]8.314\frac{\text{kg} \cdot \text{m}^2}{\text{s}^2 \cdot \text{mol} \cdot \text{K}}[/latex])
- [latex]T[/latex], kelvin or absolute temperature
- [latex]M[/latex], molar mass ([latex]\text{kg/mol}[/latex])
The implications are that heavier molecules, larger M, have a smaller urms than lighter molecules at the same temperature, and the urms of a sample of molecules increases with the square root of temperature. Note that in order to obtain urms in units of metres per second (m/s) in Equation 2, it is advisable to use the version of the gas constant R = 8.314 kg m2 s−2 mol−1 K−1 and use kg/mol as the unit for molar mass.
Optional Resource
Watch a video explanation of the kinetic-molecular theory.
Video 1 Kinetic Molecular Theory and its Postulates (6 min 59 s).
Optional Activity
If the pressure of an ideal gas is tripled at constant temperature, then the root-mean-square speed of a gas molecule:
A) increases by a factor of 3.0
B) increases by a factor of 1.7
C) remains the same
Click to see answer
The formula for the root-mean-square speed is [latex]u_{\text{rms}}=\sqrt{3RT/M}[/latex]. At constant temperature, the root-mean-square speed does not change.

