Unit 4 Acid-Base and Solubility Equilibria
4.3 Polyprotic Acids and Bases
OpenStax
Section Learning Objective
- Extend previously introduced equilibrium concepts to acids and bases that may donate or accept more than one proton.
✓ SECTION 4.3 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion. | No | 20 min |
| Optional Resource: Watch the video example of polyprotic acid equilibrium calculations. | No | 29 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 20 min |
📖 READING PORTION
Monoprotic Acids and Bases Exchange Only a Single Proton
Acids are classified by the number of protons per molecule that they can give up in a reaction. Acids such as HCl, HNO3, and HCN that contain one ionizable hydrogen atom in each molecule are called monoprotic acids. Their reactions with water are
HCl(aq) + H2O(l) ⟶ H3O+(aq) + Cl−(aq)
HNO3(aq) + H2O(l) ⟶ H3O+(aq) + NO3−(aq)
HCN(aq) + H2O(l) ⇌ H3O+(aq) + CN−(aq)
Even though acetic acid (CH3COOH) contains four hydrogen atoms, acetic acid is also monoprotic because only the hydrogen atom from the carboxyl group (−COOH) reacts with bases

Similarly, monoprotic bases are bases that will accept a single proton.
Polyprotic Acids and Bases Can Exchange More Than One Proton
Diprotic acids contain two ionizable hydrogen atoms per molecule; ionization of such acids occurs in two steps. The first ionization always takes place to a greater extent than the second ionization. For example, sulfuric acid, a strong acid, ionizes as follows
First ionization:
H2SO4(aq) + H2O(l) ⟶ H3O+(aq) + HSO4−(aq) [latex]\;\;\;[/latex] Ka1 = more than 102; complete dissociation
Second ionization:
HSO4−(aq) + H2O(l) ⇌ H3O+(aq) + SO42−(aq) [latex]\;\;\;[/latex] Ka2 = 1.2 × 10−2
This stepwise ionization process occurs for all polyprotic acids. Carbonic acid, H2CO3, is an example of a weak diprotic acid. The first ionization of carbonic acid yields hydronium ions and bicarbonate ions in small amounts. The bicarbonate ion can also act as an acid in the second ionization of carbonic acid to form hydronium ions and carbonate ions in even smaller quantities
First ionization:
H2CO3(aq) + H2O(l) ⇌ H3O+(aq) + HCO3−(aq) [latex]\;\;\;[/latex] [latex]K_{\text{H}_2\text{CO}_3} = \frac{[\text{H}_3\text{O}^+][\text{HCO}_3^−]}{[\text{H}_2\text{CO}_3]}=4.3×10^{−7}[/latex]
Second ionization:
HCO3−(aq) + H2O(l) ⇌ H3O+(aq) + CO32−(aq) [latex]\;\;\;[/latex] [latex]K_{\text{HCO}_3^-}=\frac{[\text{H}_3\text{O}^+][\text{CO}_3^{2−}]}{[\text{HCO}_3^-]}=4.7×10^{−11}[/latex]
[latex]K_{\text{a H}_2\text{CO}_3}[/latex] is larger than [latex]K_{\text{a HCO}_3^-}[/latex] by a factor of 104, so H2CO3 is the dominant producer of hydronium ion in the solution. This means that little of the HCO3− formed by the ionization of H2CO3 ionizes to give hydronium ions (and carbonate ions), and the concentrations of H3O+ and HCO3− are practically equal in a pure aqueous solution of H2CO3.
Example 1
Ionization of a Diprotic Acid
“Carbonated water” contains a palatable amount of dissolved carbon dioxide. The solution is acidic because CO2 reacts with water to form carbonic acid, H2CO3. What are [H3O+], [HCO3−], and [CO32−] in a saturated solution of CO2 with an initial [H2CO3] = 0.033 M?
H2CO3(aq) + H2O(l) ⇌ H3O+(aq) + HCO3−(aq) [latex]\;\;\;[/latex] Ka1 = 4.3 × 10−7
HCO3−(aq) + H2O(l) ⇌ H3O+(aq) + CO32−(aq) [latex]\;\;\;[/latex] Ka2 = 4.7 × 10−11
SOLUTION
As indicated by the ionization constants, H2CO3 is a much stronger acid than HCO3−, so the stepwise ionization reactions may be treated separately.
The first ionization reaction is
H2CO3(aq) + H2O(l) ⇌ H3O+(aq) + HCO3−(aq) [latex]\;\;\;[/latex] Ka1 = 4.3 × 10−7
Using provided information, an ICE table for this first step is prepared:
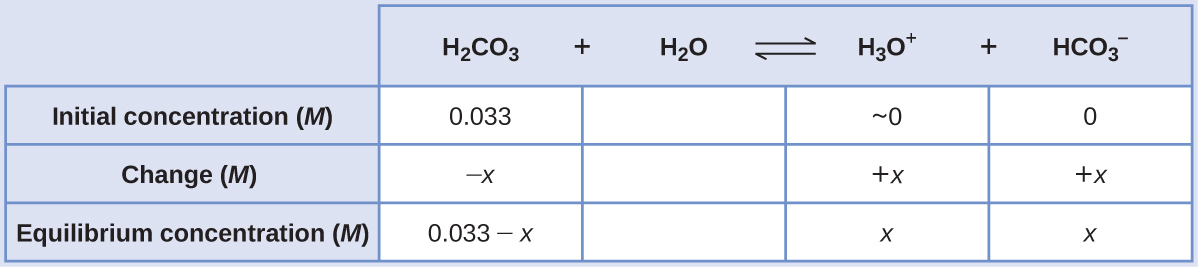
Substituting the equilibrium concentrations into the equilibrium equation gives
[latex]\begin{array}{r l} K_{\text{H}_2\text{CO}_3} = \frac{[\text{H}_3\text{O}^+][\text{HCO}_3^-]}{[\text{H}_2\text{CO}_3]} &=4.3×10^{−7} \\ \frac{x\cdot x}{0.033-x} &=4.3×10^{−7} \end{array}[/latex]
Assuming x << 0.033 and solving the simplified equation yields
x = 1.2 × 10−4
The ICE table defined x as equal to the bicarbonate ion molarity and the hydronium ion molarity
[H2CO3] = 0.033 – x ≈ 0.033 M
[H3O+] = [HCO3−] = [latex]\boxed{1.2×10^{−4} \text{ M}}[/latex]
Using the bicarbonate ion concentration computed above, the second ionization is subjected to a similar equilibrium calculation
HCO3−(aq) + H2O(l) ⇌ H3O+(aq) + CO32−(aq)
[latex]K_{\text{HCO}_3^−}=\frac{[\text{H}_3\text{O}^+][\text{CO}_3^{2−}]}{[\text{HCO}_3^−]}=\frac{(1.2×10^{−4})[\text{CO}_3^{2−}]}{1.2×10^{−4}}=4.7×10^{-11} \\ [\text{CO}_3^{2−}]=\frac{(4.7×10^{−11})(1.2×10^{−4})}{1.2×10^{−4}}=\boxed{4.7×10^{−11} \text{ M}}[/latex]
To summarize, at equilibrium [H2CO3] = 0.033 M; [H3O+] = 1.2 × 10−4 M; [HCO3−] = 1.2 × 10−4 M; [CO32−] = 4.7 × 10−11 M.
A triprotic acid is an acid that has three ionizable H atoms. Phosphoric acid is one example
First ionization:
H3PO4(aq) + H2O(l) ⇌ H3O+(aq) + H2PO4−(aq) [latex]\;\;\;[/latex] Ka1 = 7.5 × 10−3
Second ionization:
H2PO4−(aq) + H2O(l) ⇌ H3O+(aq) + HPO42−(aq) [latex]\;\;\;[/latex] Ka2 = 6.2 × 10−8
Third ionization:
HPO42−(aq) + H2O(l) ⇌ H3O+(aq) + PO43−(aq) [latex]\;\;\;[/latex] Ka3 = 4.2 × 10−13
Polyprotic bases are capable of accepting more than one hydrogen ion. The carbonate ion is an example of a diprotic base, because it can accept two protons, as shown below. Similar to the case for polyprotic acids, note the ionization constants decrease with successive ionization step. Likewise, equilibrium calculations involving polyprotic bases follow the same approaches as those for polyprotic acids.
First ionization:
H2O(l) + CO32−(aq) ⇌ HCO3−(aq) + OH−(aq) [latex]\;\;\;[/latex] Kb1 = 2.1 × 10−4
Second ionization:
H2O(l) + HCO3−(aq) ⇌ H2CO3(aq) + OH−(aq) [latex]\;\;\;[/latex] Kb2 = 2.3 × 10−8
Acid-Base Properties of Amino Acids
Proteins, such as enzymes, are made up of linear chains of amino acids that are folded precisely into three-dimensional structures. There are 22 proteinogenic amino acids that have in common a backbone structure consisting of an amine (–NH2) group and a carboxyl (–COOH) group. The amine group is basic and can accept a proton. The carboxyl group is acidic and can donate a proton. In a solution of relatively neutral pH, the backbone is a zwitterion, meaning a dipolar ion, because of the cationic, protonated amine (–NH3+) group and anionic, deprotonated carboxylate (–COO–) group.
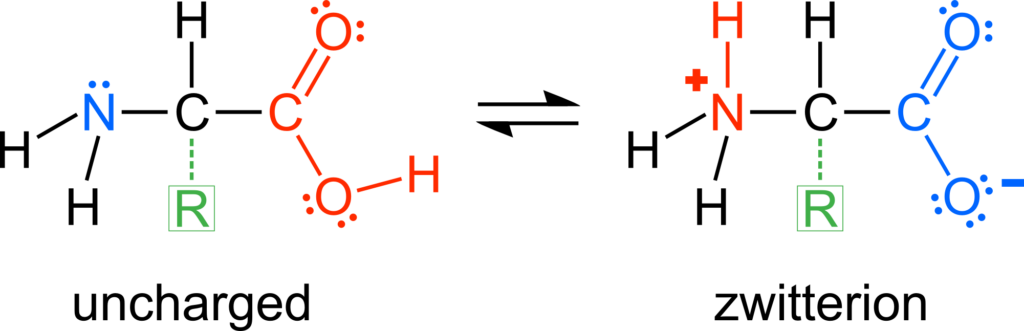
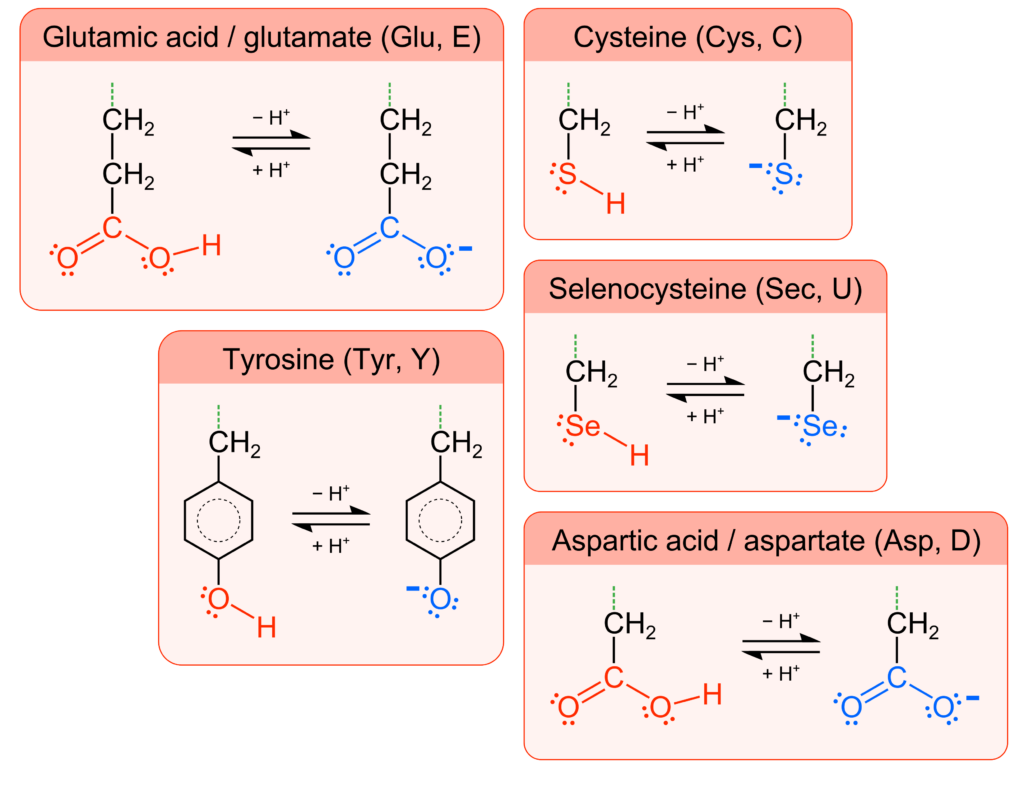
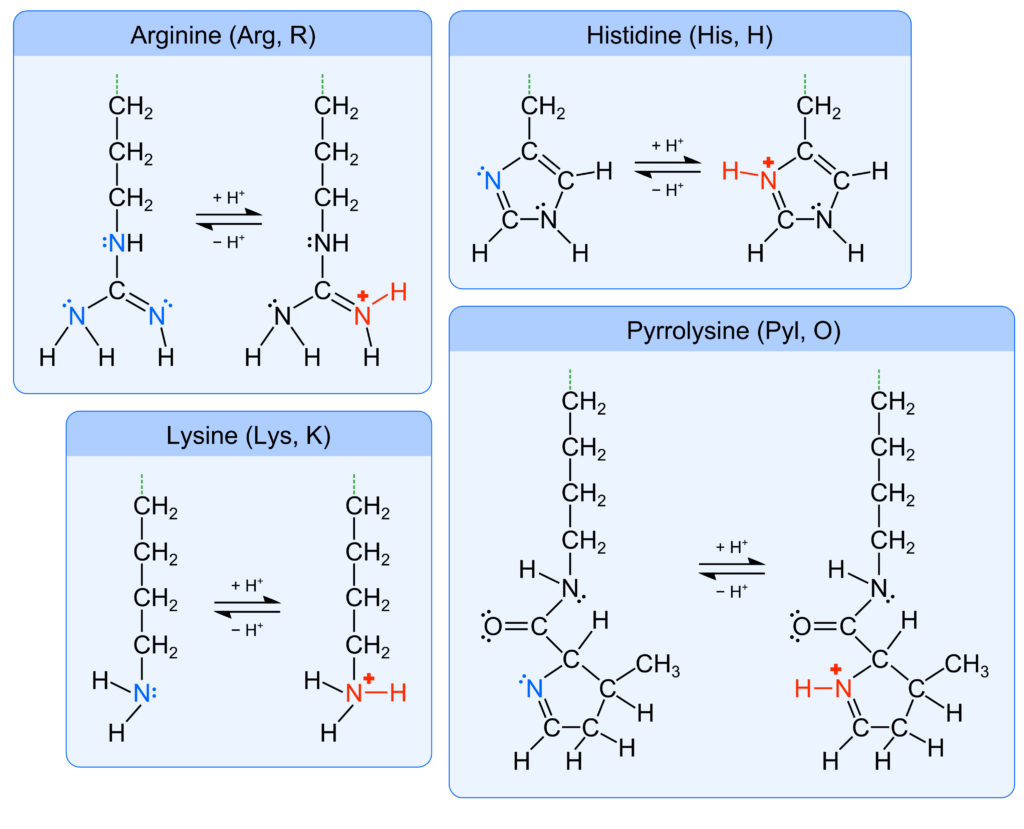
Each amino acid has a unique R-group, also called the amino acid side chain. The side chain can be acidic because of carboxyl, thiol (–SH), phenol (–C6H4OH), and selenol (–SeH) functional groups, which deprotonate to the anionic groups carboxylate, thiolate (–S−), phenolate (–C6H4O−), and selenolate (–Se−) (Figure 1). There are also amino acids with basic side chains consisting of the functional groups amine, imine (–C=N–), and guanidino (–NHCNHNH2), that can accept protons to form the respective cationic conjugate bases protonated amine, iminium (–C=NH+–), and guanidinium (–NHCNH2NH2+) (Figure 2). Therefore, an amino acid may have a nonzero net ionic charge and/or multiple atoms with a nonzero ionic charge depending on the protonation/deprotonation state of both the backbone and side chain. The amino acid side chains not listed here do not have appreciable acid-base characteristics in aqueous solution.
Optional Resource
View worked examples of polyprotic acid equilibrium calculations.
Video 1 Polyprotic Acid Base Equilibria Problems, pH Calculations Given Ka1, Ka2 & Ka3 – Ice Tables (28 min 40 s)
Salicylic acid (HOC6H4COOH) is a diprotic acid. Both functional groups of salicylic acid ionize in water, with Ka = 1.0 × 10−3 for the −COOH group and Ka = 4.2 × 10−13 for the −OH group. What is the pH of a saturated solution of the acid having 1.8 g of salicylic acid per litre of solution?
Click to see answer
[latex][\text{HOC}_6\text{H}_4\text{COOH}] = \left(\frac{1.8 \text{ g }\text{HOC}_6\text{H}_4\text{COOH}}{\text{L}}\right)\left(\frac{1\text{ mol}\text{ HOC}_6\text{H}_4\text{COOH}}{138.12 \text{ g}}\right)=0.013\text{ mol/L}[/latex]
[latex]\boxed{\begin{array}{ccccccc} \text{HOC}_6\text{H}_4\text{COOH}&+&\text{H}_2\text{O}&\rightleftharpoons&\text{HOC}_6\text{H}_4\text{COO}^− &+ &\text{H}_3\text{O}^+ \\ 0.013&&&&0&&\sim 0 \\ −x&&&&+x&&+x \\ 0.013−x&&&&x&&x \\ \end{array}}[/latex]
It is necessary to use the quadratic equation to solve the equilibrium because the concentration of the undissociated acid is close in magnitude to the Ka.
[latex]\begin{array}{r r c l} &K_{\text{a}} &=& \dfrac{[\text{HOC}_6\text{H}_4\text{COO}^−][\text{H}_3\text{O}^+]}{[\text{HOC}_6\text{H}_4\text{COOH}]} \\ \Leftrightarrow &1.0 \times 10^{-3} &=& \dfrac{x^2}{x-0.013} \\ \Leftrightarrow &(1.0 \times 10^{-3})(x-0.013) &=& x^2 \\ \Leftrightarrow &(1.0 \times 10^{-3})x-1.3 \times 10^{-5}&=&x^2 \\ \Leftrightarrow &x^2 - (1.0 \times 10^{-3})x-1.3 \times 10^{-5} &=& 0 \end{array}[/latex]
[latex]\begin{eqnarray} x&=&\dfrac{-b\pm\sqrt{b^2-4ac}}{2a} \\[5pt] &=&\dfrac{-(1.3 \times 10^{-3})\pm\sqrt{(1.0 \times 10^{-3})^2-4(1)(-1.3 \times 10^{-5})}}{2(1)} \\[5pt] &=&\dfrac{-(1.3 \times 10^{-3})\pm 7.3 \times 10^{-3}}{2} \\[5pt] &=&3.1 \times 10^{-3} \text{ M},\cancel{-4.1 \times 10^{-3}} \text{ M} \\[5pt] \end{eqnarray}[/latex]
We can calculate the concentrations as
[latex][\text{HOC}_6\text{H}_4\text{COOH}] = 0.013 \text{ M}−0.0031 \text{ M}= 0.010 \text{ M} \\ [\text{HOC}_6\text{H}_4\text{COO}^−] = [\text{H}_3\text{O}^+] = 0.0031 \text{ M}[/latex]
For the next ionization,
[latex]\boxed{\begin{array}{ccccccc} \text{HOC}_6\text{H}_4\text{COO}^-&+&\text{H}_2\text{O}&\rightleftharpoons&\text{OC}_6\text{H}_4\text{COO}^{2−} &+ &\text{H}_3\text{O}^+ \\ 0.0031&&&&0&&0.0031 \\ −x&&&&+x&&+x \\ 0.0031−x&&&&x&&0.0031+x \\ \end{array}}[/latex]
It is not necessary to solve a quadratic because the concentration of the undissociated acid is much greater than the Ka.
[latex]\begin{array}{r r c l} &K_{\text{a}} &=& \dfrac{[\text{OC}_6\text{H}_4\text{COO}^{2−}][\text{H}_3\text{O}^+]}{[\text{HOC}_6\text{H}_4\text{COO}^-]} \\ \Leftrightarrow &4.2 \times 10^{-13} &=& \dfrac{x(0.0031+x)}{0.0031-x} \\ \Rightarrow &4.2 \times 10^{-13} &\approx& \dfrac{0.0031x}{0.0031} \\ \Leftrightarrow &(4.2 \times 10^{-13})(0.0031)/0.0031&=&x \\ \Leftrightarrow &x&=&4.2 \times 10^{-13} \text{ M} \end{array}[/latex]
[latex][\text{H}_3\text{O}^+]=0.0031 \text{ M}+ x = 0.0031 \text{ M}+4.2 \times 10^{-13} \text{ M} \approx 0.0031 \text{ M}[/latex]
[latex]\text{pH} = -\log(0.0031) = \boxed{2.51}[/latex]

