Unit 4 Acid-Base and Solubility Equilibria
4.6 Solutions of Sparingly Soluble Ionic Compounds
OpenStax
Section Learning Objectives
- Write chemical equations and equilibrium expressions representing solubility equilibria.
- Carry out equilibrium computations involving solubility, equilibrium expressions, and solute concentrations.
- Describe how the common ion effect and pH affect the solubility of ionic compounds.
✓ SECTION 4.6 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion. | No | 120 min |
| Optional Resource: Watch a video on solving solubility equilibria. | No | 9 min |
| Optional Activity: Conduct a simulation on solubility equilibria. | No | 10 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 120 min |
| Complete Unit 4 Assignment on Moodle. | Yes | 120 min |
📖 READING PORTION
Solubility equilibria are established when the dissolution and precipitation of a solute species occur at equal rates. These equilibria underlie many natural and technological processes, ranging from tooth decay to water purification. An understanding of the factors affecting compound solubility is, therefore, essential to the effective management of these processes. This section applies previously introduced equilibrium concepts and tools to systems involving dissolution and precipitation.
The Solubility Product
The solubility of a substance can vary from essentially zero (insoluble or sparingly soluble) to infinity (miscible). A solute with finite solubility can yield a saturated solution when it is added to a solvent in an amount exceeding its solubility, resulting in a heterogeneous mixture of the saturated solution and the excess, undissolved solute. For example, a saturated solution of silver chloride is one in which the equilibrium shown below has been established.
[latex]\text{AgCl}(s)\;\underset{\text{precipitation}}{\overset{\text{dissolution}}{\rightleftharpoons}}\;\text{Ag}^{+}(aq)\;+\;\text{Cl}^{-}(aq)[/latex]
In this solution, an excess of solid AgCl dissolves and dissociates to produce aqueous Ag+ and Cl– ions at the same rate that these aqueous ions combine and precipitate to form solid AgCl (Figure 1). Because silver chloride is a sparingly soluble salt, the equilibrium concentration of its dissolved ions in the solution is relatively low.
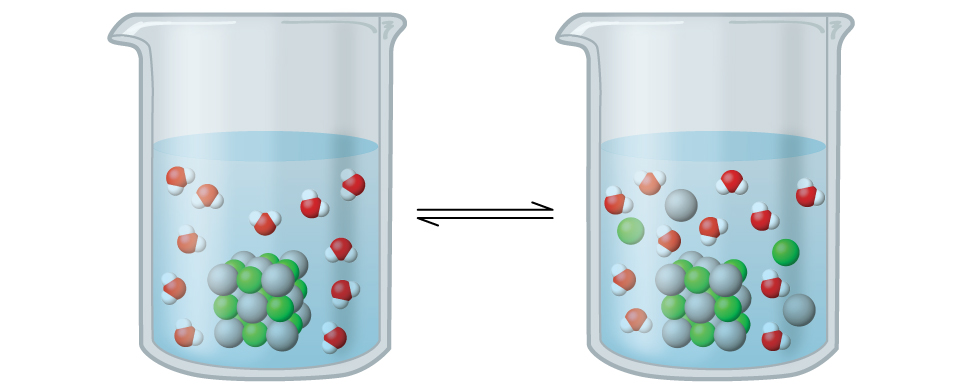
The equilibrium constant for solubility equilibria such as AgCl is called the solubility product constant (Ksp),
[latex]\text{AgCl}(s)\;{\rightleftharpoons}\;\text{Ag}^{+}(aq)\;+\;\text{Cl}^{-}(aq)\;\;\;\;\;\;\;K_{\text{sp}} = [\text{Ag}^{+}(aq)][\text{Cl}^{-}(aq)][/latex]
Recall that only gases and solutes are represented in equilibrium constant expressions, so the Ksp does not include a term for the undissolved solid AgCl. Table 1 lists the solubility product constants of some ionic compounds.
|
Substance |
Ksp at 25 °C |
|
CuCl |
1.2 × 10–6 |
|
CuBr |
6.27 × 10–9 |
|
AgI |
1.5 × 10–16 |
|
PbS |
7 × 10–29 |
|
Al(OH)3 |
2 × 10–32 |
|
Fe(OH)3 |
4 × 10–38 |
|
Table 1 Common Solubility Products by Decreasing Equilibrium Constants. Source: OpenStax Chemistry |
|
Example 1
Writing Equations and Solubility Products
Write the ionic equation for the dissolution and the solubility product expression for each of the following slightly soluble ionic compounds:
(a) AgI, silver iodide, a solid with antiseptic properties
(b) CaCO3, calcium carbonate, the active ingredient in many over-the-counter chewable antacids
(c) Mg(OH)2, magnesium hydroxide, the active ingredient in Milk of Magnesia
(d) Mg(NH4)PO4, magnesium ammonium phosphate, an essentially insoluble substance used in tests for magnesium
(e) Ca5(PO4)3OH, the mineral apatite, a source of phosphate for fertilizers
SOLUTION
(a) [latex]\text{AgI}(s)\;{\rightleftharpoons}\;\text{Ag}^{+}(aq)\;+\;\text{I}^{-}(aq)\;\;\;\;\;\;\;K_{\text{sp}} = [\text{Ag}^{+}][\text{I}^{-}][/latex]
(b) [latex]\text{CaCO}_3(s)\;{\rightleftharpoons}\;\text{Ca}^{2+}(aq)\;+\;\text{CO}_3^{2-}(aq) \;\;\;\;\;\;\;K_{\text{sp}} = [\text{Ca}^{2+}][\text{CO}_3^{2-}][/latex]
(c) [latex]\text{Mg(OH)}_2(s)\;{\rightleftharpoons}\;\text{Mg}^{2+}(aq)\;+\;2\text{ OH}^{-}(aq)\;\;\;\;\;\;\;K_{\text{sp}} = [\text{Mg}^{2+}][\text{OH}^{-}]^2[/latex]
(d) [latex]\text{Mg(NH}_4)\text{PO}_4(s)\;{\rightleftharpoons}\;\text{Mg}^{2+}(aq)\;+\;\text{NH}_4^{+}(aq)\;+\;\text{PO}_4^{3-}(aq)\;\;\;\;\;\;\;K_{\text{sp}} = [\text{Mg}^{2+}][\text{NH}_4^{+}][\text{PO}_4^{3-}][/latex]
(e) [latex]\text{Ca}_5(\text{PO}_4)_3\text{OH}(s)\;{\rightleftharpoons}\;5\text{ Ca}^{2+}(aq)\;+\;3\text{ PO}_4^{\;\;3-}(aq) \;+\;\text{OH}^{-}(aq)\;\;\;\;\;\;\;K_{\text{sp}} = [\text{Ca}^{2+}]^5[\text{PO}_4^{3-}]^3[\text{OH}^{-}][/latex]
Ksp and Solubility
The Ksp of a slightly soluble ionic compound may be simply related to its measured solubility provided the dissolution process involves only dissociation and solvation, for example
[latex]\text{M}_p\text{X}_q(s)\;{\rightleftharpoons}\;p\text{ M}^{\text{m+}}(aq)\;+\;q\text{ X}^{\text{n}-}(aq)[/latex]
In this case, we calculate the solubility product by taking the solid’s solubility expressed in units of moles per litre (mol/L), known as its molar solubility. One may derive Ksp values from provided solubilities, or vice-versa. Calculations of this sort are most conveniently performed using a compound’s molar solubility, measured as moles of dissolved solute per litre of saturated solution.
Example 2
Calculation of Ksp from Equilibrium Concentrations
Fluorite, CaF2, is a slightly soluble solid that dissolves according to the equation
[latex]\text{CaF}_2(s)\;{\rightleftharpoons}\;\text{Ca}^{2+}(aq)\;+\;2\text{ F}^{-}(aq)[/latex]
The concentration of Ca2+ in a saturated solution of CaF2 is 2.15 × 10–4 M; therefore, that of F– is 4.30 × 10–4 M, that is, twice the concentration of Ca2+. What is the solubility product of fluorite?
SOLUTION
First, write out the Ksp expression, then substitute in concentrations and solve for Ksp
[latex]\text{CaF}_2(s)\;{\rightleftharpoons}\;\text{Ca}^{2+}(aq)\;+\;2\text{ F}^{-}(aq)[/latex]
A saturated solution is a solution at equilibrium with the solid. Thus
[latex]K_{\text{sp}} = [\text{Ca}^{2+}][\text{F}^{-}]^2 = (2.15\;\times\;10^{-4})(4.30\;\times\;10^{-4})^2 = \boxed{3.98\;\times\;10^{-11}}[/latex]
As with other equilibrium constants, we do not include units with Ksp.
Example 3
Determination of Molar Solubility from Ksp
The Ksp of copper (I) bromide, CuBr, is 6.3 × 10–9. Calculate the molar solubility of copper (I) bromide.
SOLUTION
The dissolution equation and solubility product expression are
CuBr(s) ⇌ Cu+(aq) + Br−(aq) Ksp = [Cu+][Br−]
Following the ICE approach to this calculation yields the table

Substituting the equilibrium concentration terms into the solubility product expression and solving for x yields
[latex]K_{\text{sp}}=[\text{Cu}^+][\text{Br}^−] \\ 6.3×10^{−9}=(x)(x)=x^2 \\ x=\sqrt{6.3×10^{−9}} =\boxed{7.9×10^{−5}\text{ M}}[/latex]
Since the dissolution stoichiometry shows one mole of copper (I) ion and one mole of bromide ion are produced for each mole of CuBr dissolved, the molar solubility of CuBr is 7.9 × 10–5 M.
Example 4
Determination of Molar Solubility from Ksp
The Ksp of calcium hydroxide, Ca(OH)2, is 1.3 × 10–6. Calculate the molar solubility of calcium hydroxide.
SOLUTION
The dissolution equation and solubility product expression are
Ca(OH)2(s) ⇌ Ca2+(aq) + 2 OH−(aq) Ksp = [Ca2+][OH−]2
The ICE table for this system is

Substituting terms for the equilibrium concentrations into the solubility product expression and solving for x gives
[latex]K_{\text{sp}}=[\text{Ca}^{2+}][\text{OH}^−]^2 \\ 1.3×10^{−6}=(x)(2x)^2=(x)(4x^2)=4x^3 \\ x=\sqrt[3]{3.3×10^{−7}}=\boxed{{6.9×10^{−3}}\text{ M}}[/latex]
As defined in the ICE table, x is the molarity of calcium ion in the saturated solution. The dissolution stoichiometry shows a 1:1 relation between moles of calcium ion in solution and moles of compound dissolved, and so, the molar solubility of Ca(OH)2 is 6.9 × 10–3 M.
Predicting Precipitation
The equation that describes the equilibrium between solid calcium carbonate and its solvated ions is
CaCO3(s) ⇌ Ca2+(aq) + CO32−(aq) Ksp = [Ca2+][CO32−] = 8.7 × 10−9
It is important to realize that this equilibrium is established in any aqueous solution containing Ca2+ and CO32– ions, not just in a solution formed by saturating water with calcium carbonate. Consider, for example, mixing aqueous solutions of the soluble compounds sodium carbonate and calcium nitrate. If the concentrations of calcium and carbonate ions in the mixture do not yield a reaction quotient, Qsp, that exceeds the solubility product, Ksp, then no precipitation will occur. If the ion concentrations yield a reaction quotient greater than the solubility product, then precipitation will occur, lowering those concentrations until equilibrium is established (Qsp = Ksp). The comparison of Qsp to Ksp to predict precipitation is an example of the general approach to predicting the direction of a reaction first introduced in the Unit on equilibrium. For the specific case of solubility equilibria:
- Qsp < Ksp: the reaction proceeds in the forward direction (solution is not saturated; no precipitation observed)
- Qsp > Ksp: the reaction proceeds in the reverse direction (solution is supersaturated; precipitation will occur)
This predictive strategy and related calculations are demonstrated in the next few example exercises.
Example 5
Precipitation of Mg(OH)2
The first step in the preparation of magnesium metal is the precipitation of Mg(OH)2 from sea water by the addition of lime, Ca(OH)2, a readily available inexpensive source of OH–
[latex]\text{Mg(OH)}_2(s)\;{\rightleftharpoons}\;\text{Mg}^{2+}(aq)\;+\;2\text{ OH}^{-}(aq)\;\;\;\;\;\;\;K_{\text{sp}} = 8.9\times 10^{-12}[/latex]
The concentration of Mg2+(aq) in sea water is 0.0537 M. Will Mg(OH)2 precipitate when enough Ca(OH)2 is added to give a [OH–] of 0.0010 M?
SOLUTION
Calculation of the reaction quotient under these conditions is shown here
[latex]Q = [\text{Mg}^{2+}][\text{OH}^{-}]^2 = (0.0537)(0.0010)^2 = 5.4\times 10^{-8}[/latex]
Because Q is greater than Ksp (Q = 5.4 × 10–8 is larger than Ksp = 8.9 × 10–12), the reverse reaction will proceed, precipitating magnesium hydroxide until the dissolved ion concentrations have been sufficiently lowered, so that Qsp = Ksp.
Example 6
Precipitation of AgCl
Does silver chloride precipitate when equal volumes of a 2.0 × 10–4-M solution of AgNO3 and a 2.0 × 10–4-M solution of NaCl are mixed?
SOLUTION
The equation for the equilibrium between solid silver chloride, silver ion, and chloride ion
[latex]\text{AgCl}(s)\;{\rightleftharpoons}\;\text{Ag}^{+}(aq)\;+\;\text{Cl}^{-}(aq)[/latex]
The solubility product is 1.6 × 10–10.
AgCl will precipitate if the reaction quotient calculated from the concentrations in the mixture of AgNO3 and NaCl is greater than Ksp. Because the volume doubles when equal volumes of AgNO3 and NaCl solutions are mixed, each concentration is reduced to half its initial value
[latex]\frac{1}{2}(2.0\;\times\;10^{-4})\;\text{ M} = 1.0\;\times\;10^{-4}\;\text{ M}[/latex]
The reaction quotient, Q, is greater than Ksp for AgCl, so a supersaturated solution is formed.
[latex]Q = [\text{Ag}^{+}][\text{Cl}^{-}] = (1.0\;\times\;10^{-4})(1.0\;\times\;10^{-4}) = 1.0\;\times\;10^{-8}\;>\;K_{\text{sp}}[/latex]
AgCl will precipitate from the mixture until the dissolution equilibrium is established, with Q equal to Ksp.
Example 7
Concentrations Following Precipitation
Clothing washed in water that has a manganese (Mn2+) concentration exceeding 0.1 mg/L (1.8 × 10–6 M) may be stained by the manganese upon oxidation, but the amount of Mn2+ in the water can be decreased by adding a base to precipitate Mn(OH)2. What pH is required to keep [Mn2+] equal to 1.8 × 10–6 M?
SOLUTION
The dissolution of Mn(OH)2 is described by the equation
[latex]\text{Mn(OH)}_2(s)\;{\rightleftharpoons}\;\text{Mn}^{2+}(aq)\;+\;2\text{ OH}^{-}(aq)\;\;\;\;\;\;\;K_{\text{sp}} = 2.0\;\times\;10^{-13}[/latex]
We need to calculate the concentration of OH– when the concentration of Mn2+ is 1.8 × 10–6 M. From that, we calculate the pH. At equilibrium
[latex]K_{\text{sp}} = [\text{Mn}^{2+}][\text{OH}^{-}]^2[/latex]
or
[latex](1.8\;\times\;10^{-6})[\text{OH}^{-}]^2 = 2.0\;\times\;10^{-13}[/latex]
so
[latex][\text{OH}^{-}] = 3.3\;\times\;10^{-4}\;\text{ M}[/latex]
Now we calculate the pH from the pOH
[latex]\text{pOH} = -\log [\text{OH}^{-}] = -\log (3.3\;\times\;10^{-4}) = 3.48[/latex]
[latex]\text{pH} = 14.00\;-\;\text{pOH} = 14.00\;-\;3.80 = \boxed{10.52}[/latex]
If the person doing laundry adds a base, such as the sodium silicate (Na4SiO4) in some detergents, to the wash water until the pH is raised to 10.52, the manganese ion will be reduced to a concentration of 1.8 × 10–6 M; at that concentration or less, the ion will not stain clothing.
Common Ion Effect
Compared with pure water, the solubility of an ionic compound is less in aqueous solutions containing a common ion, an ion that is also produced by dissolution of the ionic compound. This is an example of a phenomenon known as the common ion effect, which is a consequence of the law of mass action that can be explained using Le Châtelier’s principle. Consider the dissolution of silver iodide
[latex]\text{AgI}(s)\;{\rightleftharpoons}\;\text{Ag}^{+}(aq)\;+\;\text{I}^{-}(aq)[/latex]
This solubility equilibrium may be shifted left by the addition of either silver or iodide ions, resulting in the precipitation of AgI and lowered concentrations of dissolved Ag+ and I–. In solutions that already contain either of these ions, less AgI may be dissolved than in solutions without these ions. This effect can also be explained in terms of mass action as represented in the solubility product expression
Ksp = [Ag+][I−]
The mathematical product of silver and iodide ion molarities is constant in an equilibrium mixture regardless of the source of the ions, and so an increase in one ion’s concentration must be balanced by a proportional decrease in the other.
Example 8
Common Ion Effect
Calculate the molar solubility of cadmium sulfide (CdS) in a 0.010-M solution of cadmium bromide (CdBr2). The Ksp of CdS is 1.0 × 10–28.
SOLUTION
The first thing you should notice is that the cadmium sulfide is dissolved in a solution that contains cadmium ions. We need to use an ICE table to set up this problem and include the CdBr2 concentration as a contributor of cadmium ions
[latex]\text{CdS}(s)\;{\rightleftharpoons}\;\text{Cd}^{2+}(aq)\;+\;\text{S}^{2-}(aq)[/latex]

[latex]K_{\text{sp}} = [\text{Cd}^{2+}][\text{S}^{2-}] = 1.0\;\times\;10^{-28}[/latex]
[latex](0.010\;+\;x)(x) = 1.0\;\times\;10^{-28}[/latex]
[latex]x^2\;+\;0.010x\;-\;1.0\;\times\;10^{-28} = 0[/latex]
We can solve this equation using the quadratic formula, but we can also make an assumption to make this calculation much simpler. Since the Ksp value is so small compared with the cadmium concentration, we can assume that the change between the initial concentration and the equilibrium concentration is negligible, so that 0.010 + x ≈ 0.010. Going back to our Ksp expression, we would now get
[latex]K_{\text{sp}} = [\text{Cd}^{2+}][\text{S}^{2-}] = 1.0\;\times\;10^{-28}[/latex]
[latex](0.010)(x) = 1.0\;\times\;10^{-28}[/latex]
[latex]x = \boxed{1.0\;\times\;10^{-26} \text{ M}}[/latex]
Check that the relative magnitude of x is, in fact, small enough to use the approximation
[latex]\begin{align*} \frac{x}{[\text{Cd}^{2+}]_{\text{initial}}}&=\frac{1.0\times10^{-26} \text{ M}}{0.010 \text{ M}} \\ &=1.0\times10^{-24} = 1.0\times10^{-22}\% < 5\% \end{align*}[/latex]
Therefore, the molar solubility of CdS in this solution is 1.0 × 10–26 M.
Effect of pH on Solubility
According to Le Châtelier’s principle, the common ion effect decreases the solubility of ionic compounds by increasing the concentration of soluble product species. Hence, the equilibrium shifts in favour of the solid ionic compound. However, we can also increase dissolution by reducing the concentration of soluble ions. As many of the anions are basic, such as carbonate, phosphate, and hydroxide, lowering pH by the addition of acids will consume basic anions. The solubility equilibrium will shift toward soluble species and increase dissolution of the solid ionic compound.
Example 9
Effects of Common Ions and pH on Solubility
What is the effect on the amount of solid Mg(OH)2 and the concentrations of Mg2+ and OH– when each of the following are added to a saturated solution of Mg(OH)2?
(a) MgCl2
(b) KOH
(c) NaNO3
(d) Mg(OH)2
(e) HCl
SOLUTION
The solubility equilibrium is
Mg(OH)2(s) ⇌ Mg2+(aq) + 2 OH−(aq)
(a) Adding a common ion, Mg2+, will increase the concentration of this ion and shift the solubility equilibrium to the left, decreasing the concentration of hydroxide ion and increasing the amount of undissolved magnesium hydroxide.
(b) Adding a common ion, OH–, will increase the concentration of this ion and shift the solubility equilibrium to the left, decreasing the concentration of magnesium ion and increasing the amount of undissolved magnesium hydroxide.
(c) The added compound does not contain a common ion, and no effect on the magnesium hydroxide solubility equilibrium is expected.
(d) Adding more solid magnesium hydroxide will increase the amount of undissolved compound in the mixture. The solution is already saturated, though, so the concentrations of dissolved magnesium and hydroxide ions will remain the same.
Q = [Mg2+][OH−]2
Thus, changing the amount of solid magnesium hydroxide in the mixture has no effect on the value of Q, and no shift is required to restore Q to the value of the equilibrium constant.
(e) Adding the acid HCl will consume the hydroxide ions produced from Mg(OH)2 and increase the solubility. The concentration of magnesium ion will increase, but the concentration of hydroxide ion will decrease.
Example 10
Effect of pH on Solubility
How does lowering the pH affect the solubility of the following ionic compounds?
(a) Ni3(PO4)2
(b) AgCl
SOLUTION
(a) The equation for the dissolution of Ni3(PO4)2 is
Ni3(PO4)2(s) ⇌ 3 Ni2+(aq) + 2 PO43−(aq)
Lowering the pH by adding acid will cause an acid-base reaction between the acid and the basic PO43−. The consumption of PO43− in acid-base reactions will shift the equilibrium toward the right and increase the solubility of Ni3(PO4)2.
(b) The equation for the dissolution of AgCl is
AgCl(s) ⇌ Ag+(aq) + Cl−(aq)
Although Cl− is the conjugate base of the strong acid HCl, Cl− has negligible basic properties in aqueous solution. Lowering the pH does not affect the equilibrium. This is a trick question!
Data Table
Solubility product constants for sparingly soluble ionic compounds (Source: OpenStax Chemistry 2e)
Optional Resource
Watch worked examples of solubility equilibria.
Video 1 Introduction to solubility equilibria (8 min 15 s).
Optional Activity
What is the molar solubility of PbCO3 (Ksp = 1.5 × 10−15, OpenStax Chemistry 2e)?
Click to see answer
[latex]\boxed{\begin{array}{c c c c} \text{PbCO}_3(s) & \longrightarrow & \text{Pb}^{2+}(aq) & + & \text{CO}_3^{2-}(aq) \\ &&0&&0 \\ &&+x&&+x \\ &&x&&x \end{array}}[/latex]
[latex]\begin{eqnarray} K_{\text{sp}}&=&[\text{Pb}^{2+}][\text{CO}_3^{2-}] \\ 1.5 \times 10^{-15}&=&x^2 \\ x&=&\sqrt{1.5 \times 10^{-15}} \\ x&=& \boxed{3.9 \times 10^{-8} \text{ mol/L}} \end{eqnarray}[/latex]
✩ UNIT 4 ASSIGNMENT
Complete Unit 4 Assignment (graded) on Moodle. This assignment is worth 11% of the course grade.

