✓ SECTION 5.5 CHECKLIST

Learning Activity	Graded?	Estimated Time
Make notes about this section’s reading portion.	No	60 min
Optional Resource: Watch a video summary of the Laws of Thermodynamics.	No	7 min
Optional Resource: Read a summary article about entropy.	No	20 min
Work on the self-check question.	No	10 min
Work on practice exercises.	No	60 min

📖 READING PORTION

In this section, consider the differences between two types of changes in a system: Those that occur spontaneously and those that occur by force. In doing so, we’ll gain an understanding as to why some systems are naturally inclined to change in one direction under certain conditions and how relatively quickly or slowly that natural change proceeds. We’ll also gain insight into how the spontaneity of a process affects the distribution of energy and matter within the system.

Spontaneous and Nonspontaneous Processes

Processes have a natural tendency to occur in one direction under a given set of conditions. Water will naturally flow downhill, but uphill flow requires outside intervention such as the use of a pump. Iron exposed to the earth’s atmosphere will corrode, but rust is not converted to iron without intentional chemical treatment. A spontaneous process is one that occurs naturally under certain conditions. A nonspontaneous process, on the other hand, will not take place unless it is “driven” by the continual input of energy from an external source. A process that is spontaneous in one direction under a particular set of conditions is nonspontaneous in the reverse direction. At room temperature and typical atmospheric pressure, for example, ice will spontaneously melt, but water will not spontaneously freeze.

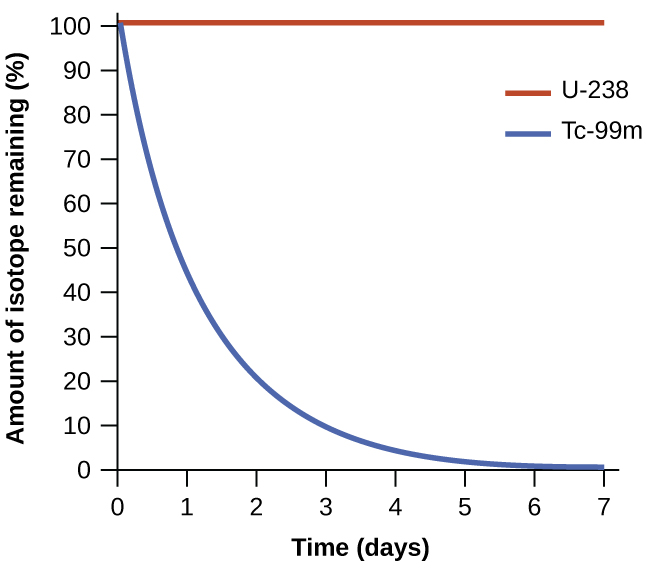
The spontaneity of a process is not correlated to the speed of the process. A spontaneous change may be so rapid that it is essentially instantaneous or so slow that it cannot be observed over any practical period of time. Radioactive decay is by definition a spontaneous process in which the nuclei of unstable isotopes emit radiation as they are converted to more stable nuclei. All the decay processes occur spontaneously, but the rates at which different isotopes decay vary widely. Technetium-99m is a popular radioisotope for medical imaging studies that undergoes relatively rapid decay and exhibits a half-life of about six hours. Uranium-238 is the most abundant isotope of uranium, and its decay occurs much more slowly, exhibiting a half-life of more than four billion years, Figure 1.

As another example, consider the conversion of diamond into graphite.

[latex]\text{C}(s\text{, diamond})\;{\longrightarrow}\;\text{C}(s\text{, graphite})[/latex]

Graphite is the stable form of this element under ambient atmospheric pressure, while diamond is the stable allotrope at very high pressures, such as those present during its geologic formation. Thermodynamic calculations indicate that the conversion of diamond to graphite at ambient pressure occurs spontaneously, yet diamonds are observed to exist, and persist, under these conditions. Though the process is spontaneous under typical ambient conditions, its rate is extremely slow, and so for all practical purposes diamonds are indeed “forever.” Situations such as these emphasize the important distinction between the thermodynamic and the kinetic aspects of a process. In this particular case, diamonds are said to be thermodynamically unstable but kinetically stable under ambient conditions.

Dispersal of Matter and Energy

As we extend our discussion of thermodynamic concepts toward the objective of predicting spontaneity, consider now an isolated system consisting of two flasks connected with a closed valve. Initially there is an ideal gas on the left and a vacuum on the right, Figure 2. When the valve is opened, the gas spontaneously expands to fill both flasks. Recalling the definition of pressure-volume work, note that no work has been done because the pressure in a vacuum is zero.

[latex]w = -P{\Delta}V = 0\;\;\;\;\;\;\;(P = 0\;\text{in a vacuum})[/latex]

Note as well that since the system is isolated, no heat has been exchanged with the surroundings (q = 0). The First Law of Thermodynamics confirms that there has been no change in the system’s internal energy as a result of this process.

[latex]{\Delta}U = q\;+\;w = 0\;+\;0 = 0[/latex]

The spontaneity of this process is therefore not a consequence of any change in energy that accompanies the process. Instead, the driving force appears to be related to the greater, more uniform dispersal of matter that results when the gas is allowed to expand. Initially, the system was comprised of one flask containing matter and another flask containing nothing. After the spontaneous process took place, the matter was distributed both more widely (occupying twice its original volume) and more uniformly (present in equal amounts in each flask).

 

Now consider two objects at different temperatures: object X at temperature T_X and object Y at temperature T_Y, with T_X > T_Y, Figure 3. When these objects come into contact, heat spontaneously flows from the hotter object (X) to the colder one (Y). This corresponds to a loss of thermal energy by X and a gain of thermal energy by Y.

[latex]q_{\text{X}}\;<\;0\;\;\;\;\;\;\;\text{and}\;\;\;\;\;\;\;q_{\text{Y}} = -q_{\text{X}}\;>\;0[/latex]

From the perspective of this two-object system, there was no net gain or loss of thermal energy, rather the available thermal energy was redistributed among the two objects. This spontaneous process resulted in a more uniform dispersal of energy.

 

As illustrated by the two processes described, an important factor in determining the spontaneity of a process is the extent to which it changes the dispersal or distribution of matter and/or energy. In each case, a spontaneous process took place that resulted in a more uniform distribution of matter or energy.

Entropy and Microstates

In 1824, at the age of 28, Nicolas Léonard Sadi Carnot published the results of an extensive study regarding the efficiency of steam heat engines. In a later review of Carnot’s findings, Rudolf Clausius introduced a new thermodynamic property that relates the spontaneous heat flow accompanying a process to the temperature at which the process takes place. This new property was expressed as the ratio of the reversible heat (q_rev) and the kelvin temperature (T). The term reversible process refers to a process that takes place at such a slow rate that it is always at equilibrium and its direction can be changed (it can be “reversed”) by an infinitesimally small change is some condition. Note that the idea of a reversible process is a formalism required to support the development of various thermodynamic concepts; no real processes are truly reversible, rather they are classified as irreversible.

Similar to other thermodynamic properties, this new quantity is a state function, and so its change depends only upon the initial and final states of a system. In 1865, Clausius named this property entropy (S) and defined its change for any process as the following:

The entropy change for a real, irreversible process is then equal to that for the theoretical reversible process that involves the same initial and final states.

Following the work of Carnot and Clausius, Ludwig Boltzmann developed a molecular-scale statistical model that related the entropy of a system to the number of microstates possible for the system. A microstate (W) is a specific configuration of the locations and energies of the atoms or molecules that comprise a system like the following:

As for other state functions, the change in entropy for a process is the difference between its final (S_f) and initial (S_i) values:

[latex]{\Delta}S = S_{\text{f}}\;-\;S_{\text{i}} = k\;\text{ln}\;W_{\text{f}}\;-\;k\;\text{ln}\;W_{\text{i}} = k\;\text{ln}\;\frac{W_{\text{f}}}{W_{\text{i}}}[/latex]

For processes involving an increase in the number of microstates, W_f > W_i, the entropy of the system increases, ΔS > 0. Conversely, processes that reduce the number of microstates, W_f < W_i, yield a decrease in system entropy, ΔS < 0.

Predicting the Sign of ΔS

The relationships between entropy, microstates, and matter/energy dispersal described previously allow us to make generalizations regarding the relative entropies of substances and to predict the sign of entropy changes for chemical and physical processes. Consider the phase changes illustrated in Figure 4. In the solid phase, the atoms or molecules are restricted to nearly fixed positions with respect to each other and are capable of only modest oscillations about these positions. With essentially fixed locations for the system’s component particles, the number of microstates is relatively small. In the liquid phase, the atoms or molecules are free to move over and around each other, though they remain in relatively close proximity to one another. This increased freedom of motion results in a greater variation in possible particle locations, so the number of microstates is correspondingly greater than for the solid. As a result, S_liquid > S_solid and the process of converting a substance from solid to liquid (melting) is characterized by an increase in entropy, ΔS > 0. By the same logic, the reciprocal process (freezing) exhibits a decrease in entropy, ΔS < 0.

 

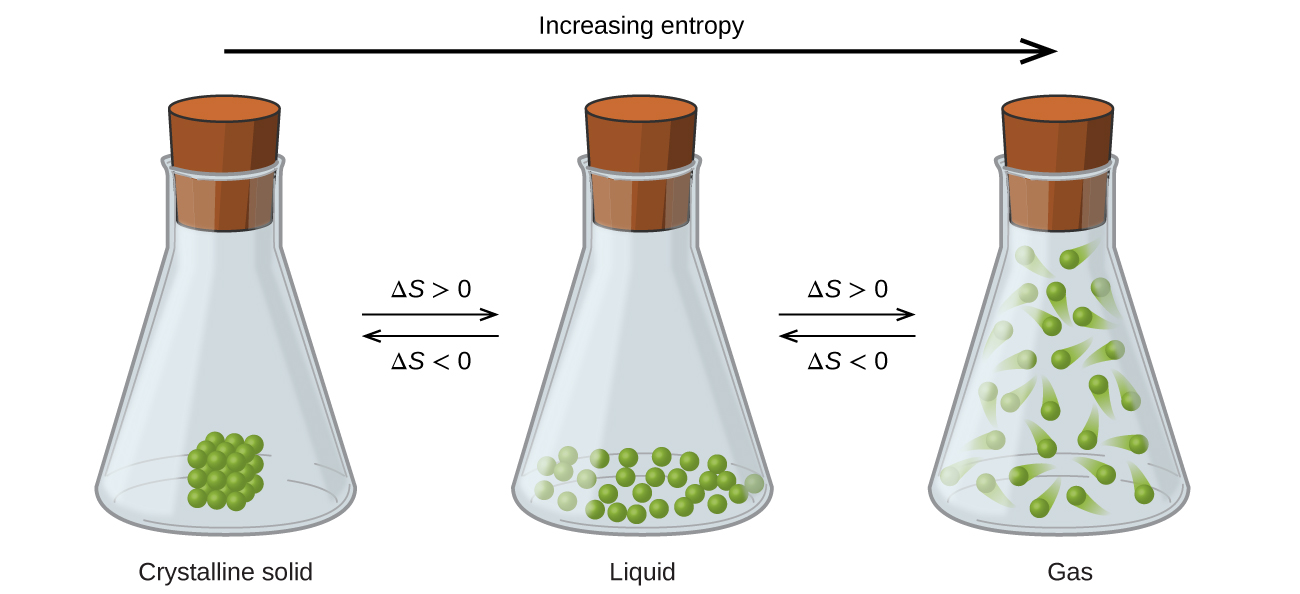
Now consider the vapour or gas phase. The atoms or molecules occupy a much greater volume than in the liquid phase; therefore, each atom or molecule can be found in many more locations than in the liquid (or solid) phase. Consequently, for any substance, S_gas > S_liquid > S_solid, and the processes of vaporization and sublimation likewise involve increases in entropy, ΔS > 0. Likewise, the reciprocal phase transitions, condensation and deposition, involve decreases in entropy, ΔS < 0.

According to kinetic-molecular theory, the temperature of a substance is proportional to the average kinetic energy of its particles. Raising the temperature of a substance will result in more extensive vibrations of the particles in solids and more rapid translations of the particles in liquids and gases. At higher temperatures, the distribution of kinetic energies among the atoms or molecules of the substance is also broader (more dispersed) than at lower temperatures. Thus, the entropy for any substance increases with temperature, Figure 5.

 

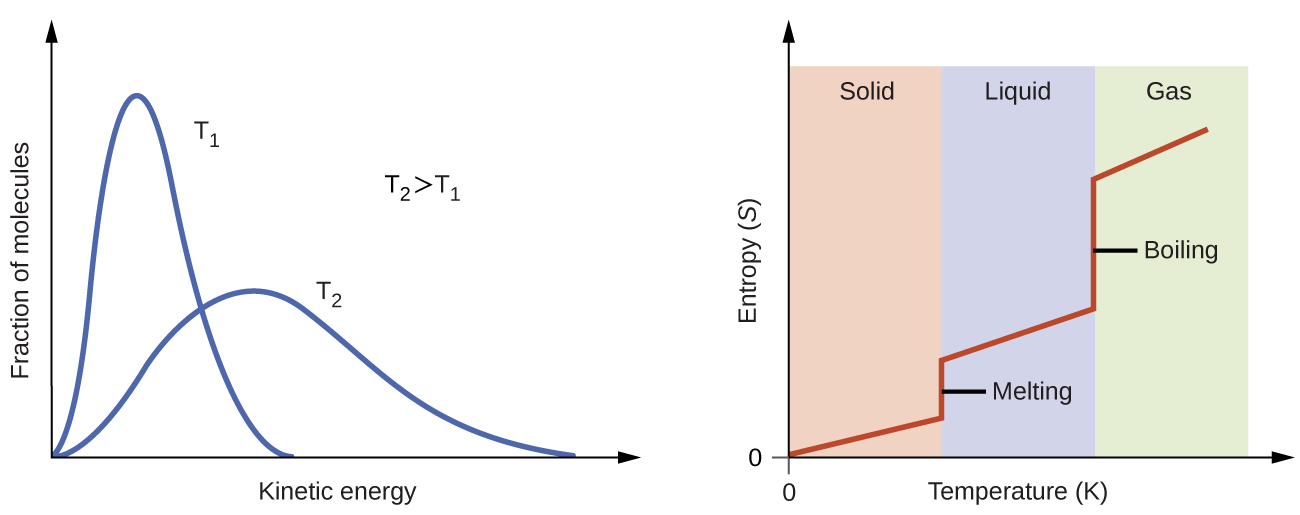
The entropy of a substance is influenced by the structure of the particles (atoms or molecules) that comprise the substance. With regard to atomic substances, heavier atoms possess greater entropy at a given temperature than lighter atoms, which is a consequence of the relation between a particle’s mass and the spacing of quantized translational energy levels (which is a topic beyond the scope of our treatment). For molecules, greater numbers of atoms (regardless of their masses) increase the ways in which the molecules can vibrate and thus the number of possible microstates and the system entropy.

Variations in the types of particles affect the entropy of a system. Compared to a pure substance, in which all particles are identical, the entropy of a mixture of two or more different particle types is greater. This is because of the additional orientations and interactions that are possible in a system comprised of nonidentical components. For example, when a solid dissolves in a liquid, the particles of the solid experience both a greater freedom of motion and additional interactions with the solvent particles. This corresponds to a more uniform dispersal of matter and energy and a greater number of microstates. The process of dissolution therefore involves an increase in entropy, ΔS > 0.

The Second Law of Thermodynamics

In the quest to identify a property that may reliably predict the spontaneity of a process, we have identified a very promising candidate: entropy. Processes that involve an increase in entropy of the system (ΔS > 0) are very often spontaneous; however, examples to the contrary are plentiful. By expanding consideration of entropy changes to include the surroundings, we may reach a significant conclusion regarding the relation between this property and spontaneity. In thermodynamic models, the system and surroundings comprise everything, that is, the universe, and so the following is true:

[latex]{\Delta}S_{\text{univ}} = {\Delta}S_{\text{sys}}\;+\;{\Delta}S_{\text{surr}}[/latex]

To illustrate this relation, consider again the process of heat flow between two objects, one identified as the system and the other as the surroundings. There are three possibilities for such a process:

1. The objects are at different temperatures, and heat flows from the hotter to the cooler object. This is always observed to occur spontaneously. Designating the hotter object as the system and invoking the definition of entropy yields the following:

[latex]{\Delta}S_{\text{sys}} = \frac{-q_{\text{rev}}}{T_{\text{sys}}}\;\;\;\;\;\;\;\text{and}\;\;\;\;\;\;\;{\Delta}S_{\text{surr}} = \frac{q_{\text{rev}}}{T_{\text{surr}}}[/latex]

2. The arithmetic signs of q_rev denote the loss of heat by the system and the gain of heat by the surroundings. Since T_sys > T_surr in this scenario, the magnitude of the entropy change for the surroundings will be greater than that for the system, and so the sum of ΔS_sys and ΔS_surr will yield a positive value for ΔS_univ. This process involves an increase in the entropy of the universe.

3. The temperature difference between the objects is infinitesimally small, T_sys ≈ T_surr, and so the heat flow is thermodynamically reversible. In this case, the system and surroundings experience entropy changes that are equal in magnitude and therefore sum to yield a value of zero for ΔS_univ. This process involves no change in the entropy of the universe.

These results lead to a profound statement regarding the relation between entropy and spontaneity known as the Second Law of Thermodynamics: all spontaneous changes cause an increase in the entropy of the universe.  In summary,

• ΔS_univ > 0 spontaneous
• ΔS_univ < 0 nonspontaneous (spontaneous in opposite direction)
• ΔS_univ = 0 reversible (system is at equilibrium)

For many realistic applications, the surroundings are vast in comparison to the system. In such cases, the heat gained or lost by the surroundings as a result of some process represents a very small, nearly infinitesimal, fraction of its total thermal energy. For example, combustion of a fuel in air involves transfer of heat from a system (the fuel and oxygen molecules undergoing reaction) to surroundings that are infinitely more massive (the earth’s atmosphere). As a result, q_surr is a good approximation of q_rev, and the Second Law may be stated as the following:

We may use this equation to predict the spontaneity of a process.

The Third Law of Thermodynamics

The previous section described the various contributions of matter and energy dispersal that contribute to the entropy of a system. With these contributions in mind, consider the entropy of a pure, perfectly crystalline solid possessing no kinetic energy (that is, at a temperature of absolute zero, 0 K). This system may be described by a single microstate, as its purity, perfect crystallinity and complete lack of motion means there is but one possible location for each identical atom or molecule comprising the crystal (W = 1). According to the Boltzmann equation (Equation 2), the entropy of this system is zero

[latex]S = k\;\text{ln}\;W = k\;\text{ln}(1) = 0[/latex]

This limiting condition for a system’s entropy represents the Third Law of Thermodynamics: the entropy of a pure, perfect crystalline substance at 0 K is zero.

We can make careful calorimetric measurements to determine the temperature dependence of a substance’s entropy and to derive absolute entropy values under specific conditions. Standard entropies are given the label [latex]S_{298}^{\circ}[/latex] for values determined for one mole of substance at a pressure of 1 bar and a temperature of 298 K. The standard entropy change (ΔS°) for any process may be computed from the standard entropies of its reactant and product species like the following:

Here, n represents stoichiometric coefficients in the balanced equation representing the process. Alternatively, the Greek letter ν (called “nu”) can be used to denote stoichiometric coefficients. For example, ΔS° for the following reaction at room temperature

[latex]a\text{A}\;+\;b\text{B}\;{\longrightarrow}\;c\text{C}\;+\;d\text{D}[/latex],

is computed as the following:

[latex]{\Delta}S^{\circ}= [cS_{298}^{\circ}(\text{C})\;+\;dS_{298}^{\circ}(\text{D})]\;-\;[aS_{298}^{\circ}(\text{A})\;+\;bS_{298}^{\circ}(\text{B})][/latex]

Similar to molar enthalpy change of a reaction (ΔH_r), the entropy change of a reaction (ΔS_r) can be expressed per mole of balanced equation. Table 1 lists some standard entropies at 298.15 K.

Substance	[latex]S_{298}^{\circ}[/latex] (J mol−1 K−1)
carbon
C(s, graphite)	5.740
C(s, diamond)	2.38
CO(g)	197.7
CO2(g)	213.8
CH4(g)	186.3
C2H4(g)	219.5
C2H6(g)	229.5
CH3OH(l)	126.8
C2H5OH(l)	160.7
hydrogen
H2(g)	130.57
H(g)	114.6
H2O(g)	188.71
H2O(l)	69.91
HCl(g)	186.8
H2S(g)	205.7
oxygen
O2(g)	205.03
Table 1 Standard Entropies (at 298.15 K, 1 atm). Source: OpenStax Chemistry 2e