Unit 1 Gases
1.1 Gas Properties
Section Learning Objectives
- Explain the physical significance, definition of, and measurement of gas pressure.
- Interpret pressure, amount, temperature, and volume as state variables.
- Convert between units of pressure and temperature.
✓ SECTION 1.1 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion and videos. | No | 60 min |
| Optional Resource: Browse the online calculator for pressure conversions. | No | 10 min |
| Work on the self-check question. | No | 5 min |
| Work on practice exercises. |
No | 45 min |
📖 READING PORTION
The Concept of Pressure
Video 1 Introduction to Atmospheric Pressure (1 min 28 sec).
The earth’s atmosphere exerts a pressure, as does any other gas. Although we do not normally notice atmospheric pressure, we are sensitive to pressure changes—for example, when your ears “pop” during take-off and landing while flying, or when you dive underwater. Video 1 gives an introduction to atmospheric pressure. Gas pressure is caused by the force exerted by gas particles colliding with the surfaces of objects. Pressure is defined as the amount of force exerted on an area. Although the force of each collision is very small, any surface of appreciable area experiences a large number of collisions in a short time, which can result in a high pressure. In fact, normal air pressure is strong enough to crush a metal container when not balanced by equal pressure from inside the container (Videos 2 and 3).
Video 2 Atmospheric pressure crushes 220 litre drum (Experiment) (2 min 39 sec).
Video 3 Explanation of the Atmospheric Pressure Crushes Oil Drum Video (1 min 18 sec).
While we associate pressure with gases, it is not a property that belongs solely to gases. Liquids exert pressure on objects submersed in them because the weight of the liquid is dispersed over the surface of the object. So, if we go to the beach and dive into the ocean, we feel the pressure of the water as we swim deeper and deeper. But if we instead decide to lie on the beach and a child starts covering us up with sand as we doze, then we feel the pressure exerted by the pile of solid sand on top of us as well. Pressure is a property independent of the phase of matter. Rather, pressure is the result of a force being applied over the surface of an object. For objects immersed in solids and liquids, it is the weight (which is just the mass of the solid or liquid subjected to the force of gravity) that is being spread out over the surface of the object. But what about an object immersed in a gas? Shouldn’t it experience a pressure? This indeed the case, as we live under a blanket of air above us that always exerts its weight over the surface of our body, even if we don’t always feel it.
Measuring Pressure

A manometer can be used to measure the (external) barometric pressure (Pbar) of the atmosphere when it forces a liquid up a cylinder with a closed end enclosing a vacuum between the closed end and the column of liquid. This type of closed end manometer is called a barometer. As the blanket of air pushes down on the liquid at the open end, the liquid rises up the tube on the closed end until the weight of air under the force of gravity is balanced by the weight of liquid under the force of gravity in the other end of the tube. In this way we can use the height of the liquid as a measure of pressure that is equivalent to that of the external blanket of air.
Most manometers historically used the liquid metal mercury in the column (Figure 1). As a metal, mercury is quite dense, and therefore we don’t need a very significant column of it to have an equivalent weight to that blanket of air with its very low density. Even so, the air can push mercury about 760 mm up the tube. This means we can use this height (and the substance it relates to) as a measure of the barometric pressure. That is, the barometric pressure is very often close to 760 mmHg. This is connected to another unit of pressure called the torr, where
1 torr ≈ 1 mmHg
We can use the same physical set up to measure the pressure of a sample of enclosed gas. Instead of a vacuum in the closed end, we could have the liquid tube connected to a sample of the gas we are interested in, while the other end is open to the atmosphere. Nature is still going to balance the pressure felt by the liquid on both sides of the tube, so the difference in height of the liquid in the tube is directly related to the difference in the pressure exerted by the gas of interest on one side and the atmospheric pressure on the other, Figure 2. If the gas pressure is higher, then liquid will be higher in the open end of the tube to provide “extra” weight to work with the atmospheric pressure to create the balance. If the atmospheric pressure is higher, then liquid will be higher on the gas sample side of things to provide additional weight to the gas pressure to balance out the atmospheric pressure. If the gas pressure equals the atmospheric pressure, then there will be no difference in height of the liquid.
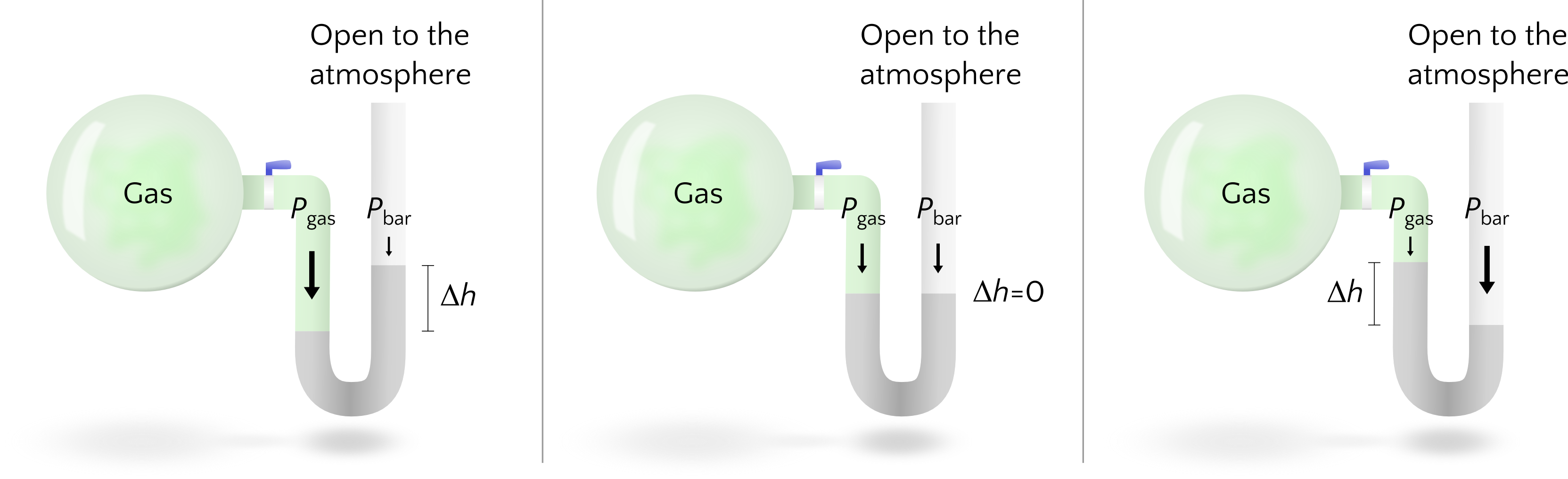
Example 1
Suppose we have a mercury manometer where the height of mercury in the open arm is 7.83 mm higher than in the closed arm. If Pbar is 748.2 mmHg, then what is Pgas in the manometer?
SOLUTION
756.0 mmHg
Having trouble figuring out this problem? Consult the following video:
Video 4 Manometer Problem Solve (2 min 49 s).
Units of Pressure

If we can use different liquids, water for example (Figure 3), to measure gas pressure, then we can technically have a different pressure unit for each liquid. For convenience, it makes sense to have a unit that is liquid independent, and we do — several of them, in fact. The prevalence of multiple units of pressure creates another challenge in that we must be very aware of the units to avoid miscalculations.
One such unit is the atmosphere (atm) which is a unit that represents an “average” of the pressure of the ever-shifting blanket of air above us into “one atmosphere’s-worth of gas pressure”. To connect atmosphere to other units of pressure,
1 atm = 760 torr = 760 mmHg
The atmosphere is a long-used unit of pressure in history and continues to appear in some American textbooks. However, the atmosphere is not the metric unit for pressure, which is the pascal (Pa). There is also a metric-based unit for the weight of the atmosphere called the bar. We see that while bar and atmosphere are not directly interchangeable, they do differ from each other by about 1.3%, and therefore are very similar to each other.
To connect bar to pascal and atmosphere, use these conversion factors:
1 bar = 105 Pa = 100 kPa
1 atm = 101 325 Pa = 101.325 kPa
From these numbers we see that:
1 atm = 1.01325 bar
1 bar = 0.98692 atm
Example 2
Perform the following pressure conversions:
- 1.00 mmHg to Pa
- 1.00 bar to torr
SOLUTION
1.00 mmHg to Pa:
[latex](1.00 \rule[0.5ex]{2.2em}{0.1ex}\hspace{-2.2em}\text{ mmHg})\left(\frac{1 \rule[0.5ex]{2.2em}{0.1ex}\hspace{-2.2em}\text{ atm}}{760 \rule[0.5ex]{2.2em}{0.1ex}\hspace{-2.2em}\text{ mmHg}}\right)\left(\frac{101325 \text{ Pa}}{1 \rule[0.5ex]{2.2em}{0.1ex}\hspace{-2.2em}\text{ atm}}\right)=\boxed{133 \text{ Pa}}[/latex]
1.00 bar to mmHg:
[latex](1.00 \rule[0.5ex]{2.2em}{0.1ex}\hspace{-2.2em}\text{ bar})\left(\frac{0.98692 \rule[0.5ex]{2.2em}{0.1ex}\hspace{-2.2em}\text{ atm}}{1 \rule[0.5ex]{2.2em}{0.1ex}\hspace{-2.2em}\text{ bar}}\right)\left(\frac{760 \text{ torr}}{\rule[0.5ex]{2.2em}{0.1ex}\hspace{-2.2em}1\text{ atm}}\right)=\boxed{750 \text{ torr}}[/latex]
Other Properties of State: Amount of Substance, Volume, and Temperature
So now we have introduced the first of the properties we can associate with any substance, but most often, for gases, and that is the pressure. This would be one of the properties of state or state variables that we can use to define the exact state of a chemical substance. Let’s formally look at all four state variables that can be used to fully describe a gas.
Pressure of the gas. We’ve seen that pressure results from a force being applied to a surface. At the microscopic level, pressure is the frequency of collisions between particles of gas with the container wall. Pressure is often expressed in units of bar, but the SI unit for pressure, the pascal is a derived unit that expresses force (expressed a newton (N) or kg m s-2) as it is spread out over an area (m2), such that
Equation 1
pressure = force / area
1 Pa = 1 N m-2 = 1 (kg m s-2) m-2
1 Pa = 1 kg m-1 s-2
Amount of gas, measured in moles. To understand something about a substance we have, we will need to know how much of it we have. If we ever want to know how many individual molecules we have, we can multiply our amount in moles by Avogadro’s number
NA = 6.022 × 1023 mol-1
Volume occupied by the gas. The volume is equivalent to the size of the container that holds the gas. While the volume is most often expressed in litres (L), volume is a derived SI unit for cubic distance, and so we might see conversion factors like
1 L = 1 dm3
1 mL = 1 cm3
1000 L = 1 m3
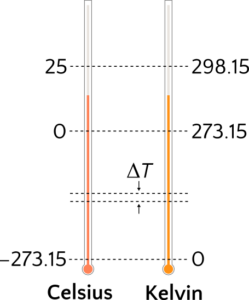
Absolute temperature of the gas, measured in kelvin (K) (Figure 4). Temperature reflects the average kinetic energy of particles of a substance. At higher temperatures particles have higher kinetic energy, which implies that they are moving faster than at lower temperature. We will see later in why we must measure our temperature in kelvin, instead of degrees Celsius (°C), as the kelvin scale for temperature sets zero temperature as the situation where the particles have no kinetic energy. The formula to convert temperature (T) from Celsius to kelvin is
Equation 2
[latex]T(\text{in K}) = T(\text{in °C}) + 273.15[/latex]
Understanding how the four state variables relate to the behaviour of gas particles is often a point of difficulty for many students, as it requires understanding the behaviours of particles you can’t see. To help with this understanding, refer to the bouncy castle analogy for understanding gas behaviours and the state variables (Figure 5 and Video 5).

Video 5 Analogy for Gas Behaviour (2 min 52 s).
Optional Resource
Pressure Converter
There is a great online tool for converting pressures from one unit to another that can be found at https://www.asknumbers.com/PressureConversion.aspx. When you look at the tool notice how many different units of pressure are available to you. This should prepare you for the idea that unit conversions for pressures are something you should practice and feel comfortable with.
The pressure of 100 kPa is equal to what pressure?
A) 1.00 atm
B) 750 torr
C) 101 325 Pa
D) 101.325 torr
Click to see answer
[latex](100 \cancel{\text{ kPa}})\left(\frac{1 \text{ atm}}{101.325 \cancel{\text{ kPa}}}\right)= 0.987 \text{ atm} \\ (100 \cancel{\text{ kPa}})\left(\frac{1 \cancel{\text{ atm}}}{101.325 \cancel{\text{ kPa}}}\right) \left(\frac{760 \text{ torr}}{1 \cancel{\text{ atm}}}\right)= 750 \text{ torr} \\ (100 \cancel{\text{ kPa}})\left(1000 \frac{ \text{Pa}}{1 \cancel{\text{ kPa}}}\right)= 1.00 \times 10^5 \text{ Pa}[/latex]
The correct answer is B) 750 torr.

