Section Learning Objectives

• Use the relationship between macroscopic gas properties via the simple gas laws and ideal gas law to solve problems.
• State the conditions for standard temperature and pressure.

✓ SECTION 1.2 CHECKLIST

Learning Activity	Graded?	Estimated Time
Make notes about this section’s reading portion and videos.	No	120 min
Optional Resources: Watch videos about gas laws.	No	17 min
Optional Activity: Play the simulation on gas behaviour.	No	30 min
Work on the self-check question.	No	5 min
Work on practice exercises.	No	65 min

📖 READING PORTION

Simple Gas Laws

We have seen that the state of a gas can be described using the four state variables of pressure, volume, temperature, and moles of gas. Early research on the behaviour of gases observed how making changes to one state variable and keeping two of the other variables constant will affect the fourth state variable. These observations led to the formulation of simple gas laws that state the mathematical relationship among the state variables.

The simple gas law called Boyle’s Law looks at how the volume of a gas changes when we vary the pressure, while keeping the amount of gas and the temperature constant.  For a fixed amount of gas at a constant temperature, the gas pressure (P) multiplied by the gas volume (V) is constant, a,

    Equation 1

[latex]PV = a[/latex]

• [latex]P[/latex], pressure (variable units)
• [latex]V[/latex], volume (variable units)
• [latex]a[/latex], constant of proportionality

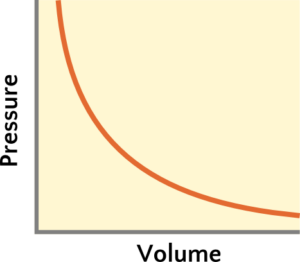
The quick overview of Boyle’s Law is one we should be familiar with: when we squeeze things (by applying more pressure), those things want to be smaller in response.  When we squeeze things less (by reducing the pressure), those things want to get bigger. If we squeeze something twice as much (by doubling the pressure), the volume will want to be smaller by half. Because the change in pressure results in a proportional change in volume, but in the opposite direction, we say there is an inversely proportional relationship between pressure and volume, P ∝ 1/V (Figure 1). According to Equation 1, as pressure increases, volume needs to decrease in order for the other side of the equation to stay constant.  Conversely, if the pressure decreases, then the volume would need to increase.  Moreover, for states 1 and 2 having different pressure and volume but same moles of gas and temperature, the result of multiplying pressure and volume stays constant at either state,

   Equation 2

[latex]P_1V_1 = P_2V_2[/latex]

• [latex]P[/latex], pressure (variable units) of state 1 or state 2
• [latex]V[/latex], volume (variable units) of state 1 or state 2

There are multiple units of pressure and volume, but consistent units must be used for state 1 and state 2.

The next simple gas law is Charles’ Law, which looks at how the volume of a gas changes when we vary the temperature while keeping constant the amount and pressure of the gas. For a fixed amount of gas at a constant gas pressure, the volume (V) divided by absolute temperature (T) is a constant, b,

Charles’ Law is a manifestation of a phenomenon that we see in everyday life that does not involve just gases.  In the universe, all substances tend to increase their volume with temperature.  We use this to our advantage in liquid-based thermometers, where the expansion of the liquid with temperature is used to measure the temperature.  Old thermostats often used two different metal strips that expand differently with temperature to measure the temperature. If we double the temperature of a gas, then we double the average kinetic energy contained by the molecules. What Charles’ Law tells us is that to ensure this additional energy is spread out to fit the constant pressure and amount of gas, the volume of the gas must double.  In other words, doubling the volume by doubling the temperature still maintains a constant distribution of energy in the container.  The gas volume is directly proportional to the absolute temperature, V ∝T. At states 1 and 2 having different volume and temperature but same moles of gas and pressure, the result of dividing volume by temperature stays constant at either state,

Note that the zero of the temperature scale must match the zero of kinetic energy for Charles’ Law to be assessed correctly.  The kelvin scale of temperature is the temperature scale that accounts for the true connection between kinetic energy and temperature, so it is the temperature scale we must use when solving gas law problems.

The third of the simple gas laws is Avogadro’s Law.  At a fixed temperature and pressure, the volume of a gas divided by the amount (n, measured in moles) of gas is a constant, c,

Once again, what the math is telling us is directly connected to our experience of the world.  If we double the amount of sand in a pile, the pile must get twice as big.  If we double the amount of water in a cup, then the volume of water must double as well.  And if we double the amount of gas in a balloon, then the volume of the balloon must double as well. There is a directly proportional relationship between the moles of gas molecules and the volume that the gas occupies, n ∝ V.  At states 1 and 2, having different moles and volume of gas but same temperature and pressure, the ratio between volume and moles is constant,

The Combined Gas Law

Now that we’ve seen how the state variables of a gas relate to each other, we can combine these behaviours to create a single gas law that contains all the information.  This is the ideal gas law,

The gas constant R encapsulates all of nature’s behaviour for substances in terms of how much kinetic energy is connected to the molecules and collects together the constants in Equations 1, 3, and 5.  We saw that temperature indicates the average kinetic energy of a molecule in a sample, and we see in the right-hand side of Equation 7 that we can scale this by the amount of molecules we have.  That is, amount of substance and the temperature the substance is at is connected to the total kinetic energy of the entire sample.  The gas constant R tells us how that total energy is intimately connected to the state variables of a substance.  More correctly, since for an ideal gas the only possible type of energy is the kinetic energy of the molecules, then the total kinetic energy content of a given amount of an ideal gas is completely determined by the temperature of the gas and not the other two state variables.  This is why part of the units of R are “per kelvin per mol”.

We always measure T in kelvin and n in moles, but P and V can often be expressed in many different units, therefore the gas constant R can appear to have many different values depending on the units of P and V.  Therefore, the value of the gas constant R can be different, depending on how we measure the pressure and volume.  Some more useful values of R that we are likely to encounter are

0.083145 L bar K^-1 mol^-1

0.082057 L atm K^-1 mol^-1

8.3145 L kPa K^-1 mol^-1

8.3145 J K^-1 mol^-1

To better understand why this “constant” can have different values depending on how we measure pressure and volume, consult Video 2.

Video 2 Different Units for the Gas Constant R (3 min 44 s).

To practice using the ideal gas equation and to understand the importance of choosing the right value of R, try the following example.

There is also a more powerful form of the ideal gas equation called the general ideal gas equation.  If we rearrange the ideal gas law to solve for R, then

In other words, the ratio of pressure times volume with respect to amount times temperature for any ideal gas at equilibrium is constant.  This allows us to look at an ideal gas undergoing changes in one, two, or three of the state variables at the same time and allows us to solve for the fourth state variable in one calculation.  Consider some sample of an ideal gas before some changes take place.  The state variables describing the gas must maintain the ratio seen above (since it equals the constant, R) regardless of any changes made in state, so                                                                         

Standard Temperature and Pressure

We’ve now seen that we can describe any gas through the four state variables.  However, there are a near-infinite combinations of those variables that maintain the relationship that is defined by the ideal gas law.  It then makes sense for us to have a common comparison point for us all to build our understanding and intuition of gas behaviour based on some common everyday situation. To do this, we define a set of standard conditions that we call standard temperature and pressure (STP) where

T = 0 ˚C = 273.15 K and P = 1 atm

The International Union of Pure and Applied Chemistry recommends 1 bar as standard pressure, but practically, many people use 1 atm.

If we choose our constant temperature and pressure to be STP, then Avogadro’s Law tells us the volume of some given amount of ideal gas will be a constant.  If we choose 1 mole of gas as this amount, then the molar volume (V_m) of a gas is

V_m = 22.4 L mol^-1 at STP

An important aspect of this idealized behaviour is that the identity of the gas does not matter.  When we treat a gas ideally, its identity is irrelevant in regards to its behaviour, because we ignore the intermolecular forces that would be different for differing molecular identities.  Therefore, all ideal gases have the same molar volume at the same temperature and pressure (Figure 2).

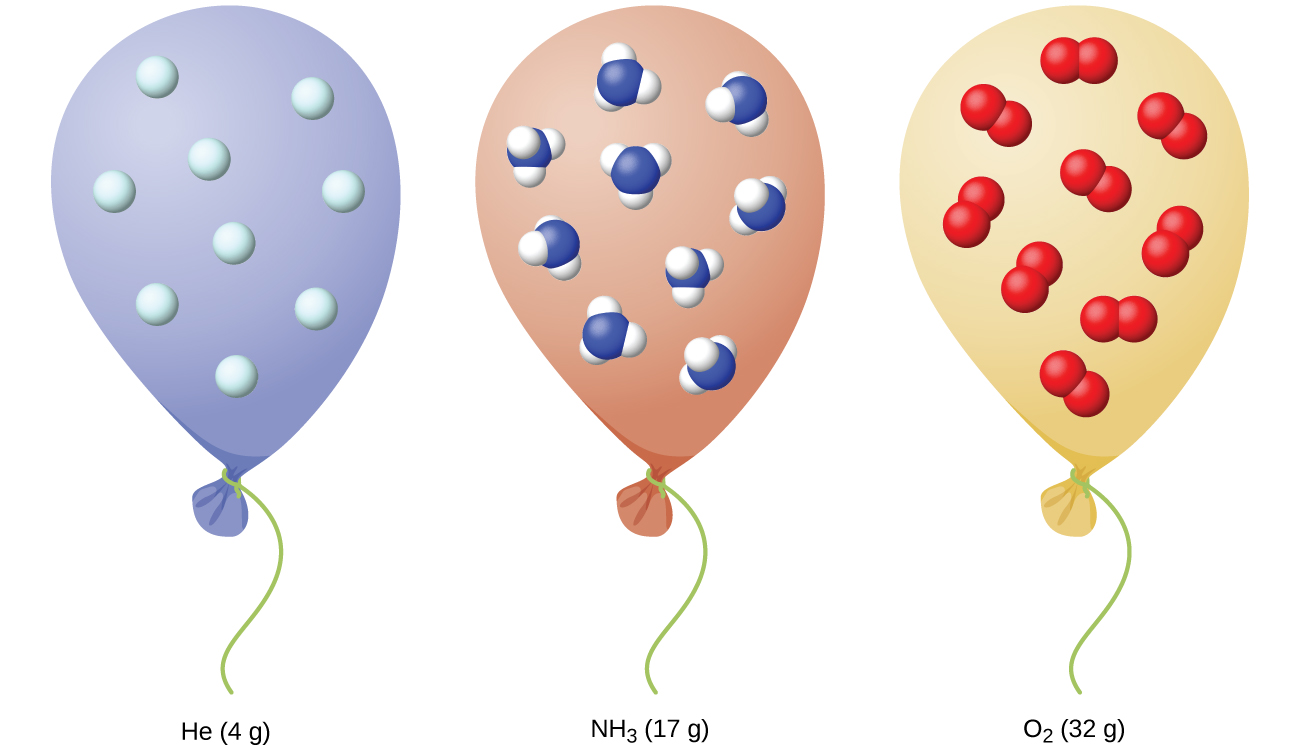
If we take our V_m = 22.4 L mol^-1 at STP and increase the temperature to 298.15 K (25.00 °C), we know the gas will expand to a new volume for the same pressure and gas amount.  This molar volume of the ideal gas is

V_m = 24.5 L mol^-1 at 298.15 K and 1 atm

This is a useful number to remember to develop your intuition about volumes of gases when we talk about reactions at everyday conditions.  This volume is about the same size as a round 36 cm (14 inch) diameter balloon, or about 3 ½ regulation basketballs, or about half of the volume of a typical car’s gas tank.  Try and find a comparison volume from how you experience your life to give your mind a picture of this size that you can use to compare to calculated volumes at similar conditions.

Limitations of the Ideal Gas Assumption

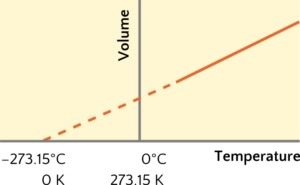
There is one thing we didn’t discuss with Charles’ Law.  Simply, if we cool down a gas enough, the attractive intermolecular forces between the molecules will eventually take hold and the gas will condense to a liquid.  Charles’ Law extrapolates the behaviour graphically to zero kelvin temperature without taking this reality into account (Figure 3).  In other words, Charles’ Law assumes the gas will never condense to a liquid, because there are no intermolecular forces between molecules. The simple gas laws are reflecting an idealized behaviour of gas molecules that can be summed up as the description of a sample of an ideal gas.  An ideal gas has four simple properties:

1. The molecules of the gas occupy no volume. (They can occupy the same space!)
2. There are no intermolecular forces between gas molecules. (No attractive or repulsive interactions!)
3. The gas molecules are in constant random motion and collide elastically. (No net change in total energy of the gas!)
4. The gas has achieved a state of equilibrium (n, P, T and V are all constant!).

Nonideal gas behaviour becomes more apparent as temperature decreases and pressure increases.  Thus, the ideal gas law is inaccurate in circumstances of low temperature and high pressure and is more suitable for gases at high temperature and low pressure.

For a more detailed discussion of these properties, you can watch the following video:

Video 5 Ideal Gas Properties (3 min 37 s).