Unit 1 Gases
1.4 Graham’s Law of Diffusion and Effusion
OpenStax
Section Learning Objective
- Apply the ideas of the kinetic-molecular theory to the concepts of effusion and diffusion.
✓ SECTION 1.4 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion and videos. | No | 60 min |
| Optional Resources: Read and watch videos about diffusion and effusion. | No | 60 min |
| Optional Activity: Play the diffusion simulation. | No | 10 min |
| Work on the self-check question. | No | 5 min |
| Work on practice exercises. | No | 20 min |
📖 READING PORTION
The Bulk Movement of Particles
Consider what happens when you put a drop of food colouring (or drink flavour drops) into a glass of water. You eventually see the high concentration drop of colour mix throughout the colourless water until you get a solution where any given part has the exact same color as any other part.
A similar phenomenon occurs for gases. If you have experienced the smell of food or perfume wafting through the air, you have been aware of how gas particles can spread throughout a room. The movement of gas is due to the random motion of particles as they could travel hundreds of metres per second on average and collide with other particles every billionth of a second or so (1 × 10−9 s = 1 ns). There are two different phenomena related to the bulk movement and mixing of gases that come from all those collisions and constant random motion (Figure 1). Diffusion is the migration of particles over a distance due to the random motion of the particles. Effusion is when randomly moving particles escape a container through a small hole in the container.
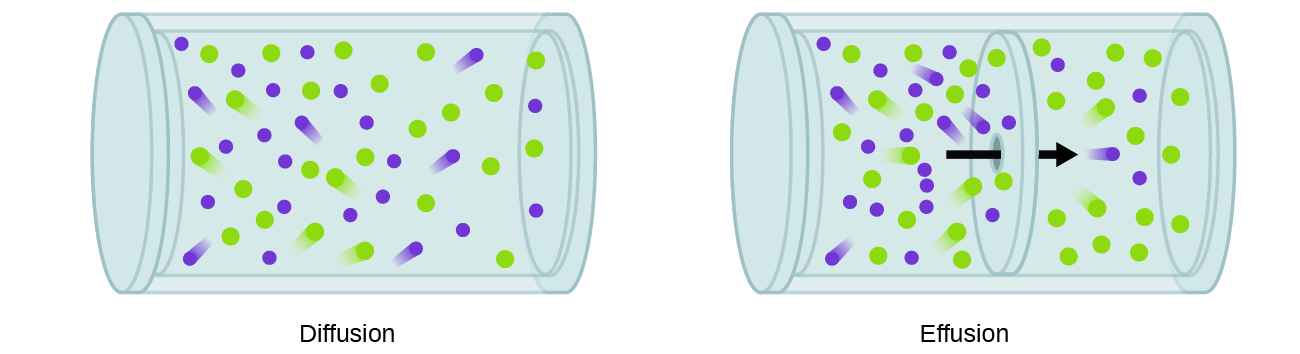
How quickly diffusion and effusion occur depends on the particle speed of a gas. The particle speed of a gas, as in the root-mean-square speed, varies with temperature and molar mass of the gas. We can determine a formula for the molar mass of a gas using the ideal gas law. The molar mass (M) is the amount of mass (m) per mole (n) of substance, M = m/n and equivalently n = m/M. We can substitute n = m/M into the ideal gas law PV = nRT as
[latex]PV = \dfrac{m}{M}RT[/latex]
and solving for molar mass explicitly
Equation 1
[latex]M = \dfrac{mRT}{PV}[/latex]
- [latex]M[/latex], molar mass ([latex]\text{g/mol}[/latex])
- [latex]m[/latex], mass ([latex]\text{g}[/latex])
- [latex]R[/latex], gas constant (variable units)
- [latex]T[/latex], kelvin or absolute temperature
- [latex]P[/latex], pressure (variable units)
- [latex]V[/latex], volume (variable units)
The units of pressure and volume must match the units in the appropriate form of the gas constant.
Moreover, we can connect the molar mass of a gas with the density of the gas. Density (d) is the mass (m) of substance per unit volume (V) as d = m/V. We can rearrange Equation 1 as
[latex]M = \dfrac{m}{V}\dfrac{RT}{P}[/latex]
[latex]M = \dfrac{dRT}{P}[/latex]
and solving for density explicitly
Equation 2
[latex]d = \dfrac{PM}{RT}[/latex]
- [latex]d[/latex], mass density (variable units)
- [latex]P[/latex], pressure (variable units)
- [latex]M[/latex], molar mass ([latex]\text{g/mol}[/latex])
- [latex]R[/latex], gas constant (variable units)
- [latex]T[/latex], kelvin or absolute temperature
The units of pressure, volume, and density must match the units in the appropriate form of the gas constant.
If these steps don’t seem clear to you, consider this video walking you through the derivations
Video 1 Getting the Molar Mass of a Gas from its Density (2 min 41 s).
Example 1
The density of an unknown ideal gas CxHy is 1.15 g/L at 20⁰C and 1.00 bar. What is the molecular formula of the gas?
SOLUTION
We can identify the unknown gas by calculating its molar mass. The subscripts x and y will be whole numbers such that the molar mass of the formula will match the calculated molar mass. Equations 1 and 2 both involve molar mass. However, without knowing explicitly the volume of the gas but given the density of the gas, Equation 2 is more convenient to use. Because the pressure is measured in bar, use the gas constant R as 0.083145 L bar K-1 mol-1
[latex]\begin{eqnarray} d&=&\frac{PM}{RT} \\[0.5em] M&=&\frac{dRT}{P} \\[0.5em] &=&\frac{(1.15 \text{ g/L})(0.083145 \text{ L} \cdot \text{bar} \cdot \text{K}^{-1} \cdot \text{mol}^{-1})(20+273.15)\text{K}}{1.00 \text{ bar}} \\[0.5em] &=&28.0 \text{ g/mol} \end{eqnarray}[/latex]
From the bonding rules in CHEM 1503, we know that carbon takes an octet of electrons, and hydrogen takes a duet. Guess whole numbers of x and y according to bonding rules and check if the molar mass is 28.0 g/mol. Start with small numbers because the molar mass is not that large
- x = 1, y = 4 [latex]\Rightarrow[/latex] methane, C1H4:
[latex]M=(1)(12.01 \text{ g/mol})+(4)(1.01 \text{ g/mol})=16.05 \text{ g/mol}[/latex]
The molar mass 16.05 g/mol is below the calculated 28.0 g/mol. Increase the number of atoms
- x = 2, y = 6 [latex]\Rightarrow[/latex] ethane, C2H6:
[latex]M=(2)(12.01 \text{ g/mol})+(6)(1.01 \text{ g/mol})=30.08 \text{ g/mol}[/latex]
The molar mass 30.08 g/mol is just above the calculated 28.0 g/mol. Decrease the number of atoms. We cannot do much about the number of carbons. We may decrease the number of hydrogen atoms
- x = 2, y = 4 [latex]\Rightarrow[/latex] ethene, C2H4:
[latex]M=(2)(12.01 \text{ g/mol})+(4)(1.01 \text{ g/mol})=28.06 \text{ g/mol}[/latex]
The molar mass 28.06 g/mol agrees with the calculated 28.0 g/mol within rounding error. Therefore, the unknown gas is ethene.
Chemistry in Real Life
How ᐃᒡᓗᐃᑦ Keep Warm
The Inuktitut word ᐃᒡᓗ (iglu, also spelled igloo) refers to a house. Popular culture may interpret the iglu as a hut made specifically of snow. Snow igluit (plural of iglu, ᐃᒡᓗᐃᑦ in Inuktitut) are constructed such that the entrance is connected to the living area by a passageway below ground level. This design maintains the warmth inside the iglu from the residents’ body heat and lit qulliq. The qulliq is an oil lamp that is further discussed in Section 5.2. The temperature outside may be −30°C but the air inside the iglu is often around 20°C.1 Cold air is heavier (denser) and sinks below warm air. Hence, cold air from the entrance can sink down the lower passageway and the living area is elevated to the level of warm air. We can calculate the difference in density between cold (−30°C) and warm (20°C) air as follows.
Let the atmospheric pressure be 1.00 atm and use the form of the gas constant [latex]R = 0.08206 \text{ L⋅atm⋅mol}^{-1}\text{⋅K}^{-1}[/latex]. Air is a mixture of approximately 78.1% nitrogen, 21.0% oxygen, and 0.9% argon.1 The average molar mass of air is
[latex]M = 0.781(28.02 \text{ g/mol}) + 0.210(32.00 \text{ g/mol}) + 0.009(39.95 \text{ g/mol}) = 28.96 \text{ g/mol}[/latex]
We can use the average molar mass of air and the ideal gas law to calculate the density of air,
[latex]\begin{eqnarray} PM &= dRT \\ d &= \frac{PM}{RT}\end{eqnarray}[/latex]
At −30°C,
[latex]d = \frac{(1.00 \text{ atm})(28.96 \text{ g/mol})}{0.08206 \text{ L⋅atm⋅mol}^{-1}\text{⋅K}^{-1}(-30 + 273.15)\text{ K}} = 1.45 \text{ g/L}[/latex]
At 20°C,
[latex]d = \frac{(1.00 \text{ atm})(28.96 \text{ g/mol})}{0.08206 \text{ L⋅atm⋅mol}^{-1}\text{⋅K}^{-1}(20 + 273.15)\text{ K}} = 1.20 \text{ g/L}[/latex]
The percent difference is
[latex]\frac{1.45 \text{ g/L} - 1.20 \text{ g/L}}{1.20 \text{ g/L}} = 20.8\%[/latex]
Cold air is 20.8% denser than warm air.
1https://uwaterloo.ca/chem13-news-magazine/december-2019/feature/snow-making-life-possible-arctic
Graham’s law states that the rate of diffusion or effusion both vary inversely with the molar mass of the gas. The heavier the gas particles, the slower the gas travels through space. Comparing two different gases at the same temperature and pressure, Graham’s law is stated as
Equation 3
[latex]\frac{\text{rate}_A}{\text{rate}_B} = \sqrt{\frac{\text{molar mass}_B}{\text{molar mass}_A}}[/latex]
and in terms of density,
Equation 4
[latex]\frac{\text{rate (diffusion or effusion) of gas A}}{\text{rate (diffusion or effusion) of gas B}} = \sqrt{\frac{\text{density of gas B}}{\text{density of gas A}}}[/latex]
Example 2
An inept researcher, who had set up a system of remote-controlled stopcocks on gas cylinders stored at one end of the laboratory, inadvertently pushed the button that allowed a small opening in two of the cylinders. One cylinder contained hydrogen cyanide (HCN) gas, and the other cylinder contained dinitrogen oxide (N2O). Which gas reaches the researcher first?
SOLUTION
Assume that both gases had the same distance to travel as they diffused towards the researcher.
molar mass HCN = 27.0 g mol–1, molar mass N2O = 44.0 g mol–1
Substituting into Graham’s law,
[latex]\frac{\text{rate of diffusion HCN}}{\text{rate of diffusion N}_2\text{O}}[/latex]
[latex]= \sqrt{\frac{\text{molar mass N}_2\text{O}}{\text{molar mass HCN}}}[/latex]
[latex]= \sqrt{\frac{44.0 \text{ g mol}^{–1}}{27.0 \text{ g mol}^{–1}}}[/latex]
[latex]= 1.28[/latex]
Since HCN diffuses 1.28 times faster than N2O, HCN will reach the researcher first.
Example 3

Nitrogen gas and sulfur dioxide gas are placed in individual bulbs, whose taps are connected by a 10.0 m pipe, Figure 2. Both gases are at the same pressure, temperature, and volume. The taps are opened at the same time.
(a) If nitrogen gas effuses at 79 mL/s, what is the rate of effusion of sulfur dioxide?
(b) At what distance from the nitrogen tap will the two gases meet?
SOLUTION
(a) Using Equation 3
\begin{eqnarray} \dfrac{\text{rate}_{\text{ N}_2}}{\text{rate}_{\text{ SO}_2}}&=&\sqrt{\dfrac{\text{molar mass}_{\text{ SO}_2}}{\text{molar mass}_{\text{ N}_2}}} \\[0.5em] \text{rate}_{\text{ SO}_2}&=&\dfrac{\text{rate}_{\text{ N}_2}}{\sqrt{\dfrac{\text{molar mass}_{\text{ SO}_2}}{\text{molar mass}_{\text{ N}_2}}}} = \dfrac{79 \text{ mL/s}}{\sqrt{\dfrac{64.07 \text{ g/mol}}{28.02 \text{ g/mol}}}}=\boxed{52 \text{ mL/s}} \end{eqnarray}
(b) Find the ratio of the rates of effusion
[latex]\dfrac{\text{rate}_{\text{ N}_2}}{\text{rate}_{\text{ SO}_2}}=\sqrt{\dfrac{\text{molar mass}_{\text{ SO}_2}}{\text{molar mass}_{\text{ N}_2}}} = \sqrt{\dfrac{64.07 \text{ g/mol}}{28.02 \text{ g/mol}}} = 1.512[/latex]
Nitrogen effuses 1.512 times faster than sulfur dioxide. When nitrogen effuses a distance of 1.512x, sulfur dioxide will only effuse a distance of x. The total distance is 1.512x + x = 2.512x. Here, the total distance is 10.0 m. Solving for x
[latex]\begin{eqnarray} 2.512x&=&10.0\text{ m} \\ x&=&3.98 \text{ m} \end{eqnarray}[/latex]
The distance that nitrogen effuses is
[latex]1.512x=1.512(3.98 \text{ m}) = \boxed{6.02 \text{ m}}[/latex]
When you are doing Graham’s law calculations, remember that “rate” is not the same thing as “time.” That is,
Equation 5
[latex]\text{rate} = \frac{\text{amount of gas transferred}}{\text{time}}[/latex]
Example 4
It takes 243 s for 4.46 × 10−5 mol Xe to effuse through a tiny hole. Under the same conditions, how long will it take 4.46 × 10−5 mol Ne to effuse?
SOLUTION
Starting with Graham’s law, Equation 3
[latex]\frac{\text{rate of effusion of gas Xe}}{\text{rate of effusion of gas Ne}} = \frac{\sqrt{\mathcal{M}_\text{Ne}}}{\sqrt{\mathcal{M}_\text{Xe}}}[/latex]
substitute in Equation 5
To get:
Noting that amount of A = amount of B, and solving for time for Ne:
and substitute values:
Finally, solve for the desired quantity:
Note that this answer is reasonable: Since Ne is lighter than Xe, the effusion rate for Ne will be larger than that for Xe, which means the time of effusion for Ne will be smaller than that for Xe.
Optional Resources
For more detail on diffusion versus effusion, read this article.
Watch the following video introducing the concepts of effusion and diffusion and how they are tied to the velocity of gas molecules
Video 2 Passing Gases: Effusion, Diffusion, and the Velocity of a Gas – Crash Course Chemistry #16 (11 min 25 s).
Optional Activity
Explore diffusion by using the PhET Gas Properties simulator. Choose the “Diffusion” Simulation. Expand the Data section by clicking the plus sign. This section will give you amount data for each type of particle in each half of the container and the average temperature in that half of the container, based on the particles and their speed.
- Perform a simulation where you put gas particles in only one side of the box and remove the divider to observe the tendency of a gas to expand against a vacuum to fill the container. Note the temperature readings over time.
- Perform several simulations using an equal number of particles on each side and then “Remove Divider”. Consider starting with different masses, radii, and temperatures on each side. Remove the divider and track the changes in data, especially the temperature. If you started with different temperatures but equal particles on each side, notice that once the divider is removed the tendency is for the temperature throughout the box to even out to the average of the two original temperatures. This is the tendency of nature to spread the energy out as evenly as possible when it starts from an imbalanced energy distribution.
The density of a gas sample is 1.00 g L-1 at 109 degrees Celsius and 0.980 atm. What is the molar mass of the gas?
A) 9.13 g mol-1
B) 0.0313 g mol-1
C) 32.0 g mol-1
D) 0.110 g mol-1
Click to see answer
Density and molar mass are related by the equation [latex]d=\frac{PM}{RT}[/latex]. Rearrange the equation to solve for molar mass. The temperature is [latex]T=109^\circ \text{C}+273.15=382 \text{ K}[/latex]. Use the gas constant [latex]R= 0.082057 \frac{\text{L} \cdot \text{atm}}{\text{K} \cdot \text{mol}}[/latex].
[latex]\begin{align*} d&=\dfrac{PM}{RT} \\ M&=\dfrac{dRT}{P} \\ &=\dfrac{\left(1.00 \frac{\text{g}}{\text{L}}\right)\left(0.082057\frac{\text{L} \cdot \text{atm}}{\text{K} \cdot \text{mol}}\right)(382 \text{ K})}{0.980 \text{ atm}} \\ &=32.0 \text{ g/mol} \\ \end{align*}[/latex]

