Unit 1 Gases
1.5 Gas Phase Reactions and Mixtures of Gases
OpenStax
Section Learning Objectives
- Perform stoichiometric calculations for gas phase reactions.
- Relate the mole fraction and partial pressure and partial volume of a particular gas in a mixture to its contribution to the total pressure and total volume.
✓ SECTION 1.5 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion and videos. | No | 60 min |
| Optional Resource: Read about Dalton’s law and collecting gas over water. | No | 15 min |
| Work on the self-check question. | No | 5 min |
| Work on practice exercises. | No | 60 min |
| Complete Unit 1 Assignment on Moodle. | Yes | 120 min |
📖 READING PORTION
Volume and Pressure are Additive for Ideal Gases
Now that we have the power of the ideal gas law, if we treat any gases in a chemical reaction of interest as ideal gases, then we can use the ideal gas equation and the balanced equation of the reaction to solve reaction stoichiometry problems, if we know something about the other state variables of the gas.
Challenge yourself by seeing if you can use the ideal gas law in trying to solve the following example.
Example 1
How many grams of Na(l) are produced per liter of N2(g) at 25 ˚C and 1.0 bar?
2 NaN3(s) → 2 Na(l) + 3 N2(g)
SOLUTION
n = 0.040 mol of N2(g) in 1 L at the given T and P so m = 0.64 g of Na(l) per litre of N2(g) produced.
Having trouble figuring out this problem? Consult the following video:
Video 1 Gas Stoichiometry (4 min 56 s).
If you solved the problem, then you have done something very similar to chemical problem solving from balanced equations in the past. In past problems, you would take a known mass of a chemical, use its molar mass to calculate the number of moles, and then tie that through reaction stoichiometry to a number of moles of a different chemical in the reaction, and perhaps its mass, after using its molar mass. Here, when the chemical is a gas, the steps are all the same except you calculate the number of moles of gas using a known pressure, temperature, and volume. Then you can use reaction stoichiometry and connect to the moles of another chemical. If that chemical is a gas, you should be able to determine a property like its pressure of volume using the ideal gas law.
This can be very powerful for us in that we can sometimes take shortcuts to find pieces of information. For instance, consider chemical reactions involving all gases occurring in a balloon at a given constant pressure and temperature, which would be a common occurrence in a chemistry laboratory. Because the pressure and temperature are constant, Avogadro’s Law tells us the amount of a particular gas in the balloon is directly tied to the volume that gas contributes to the balloon’s overall volume. This is the Law of Combining Volumes, where the ratios of volumes of the gases match the stoichiometric ratios of the gases.
Consider the reaction
2 NO(g) + O2(g) → 2 NO2(g)
The reaction stoichiometry tells us that for every oxygen molecule consumed in the reaction, two nitric oxide molecules are consumed, and two nitrogen dioxide molecules are formed. But remember, stoichiometry can be scaled, so we could talk about dozens of molecules or moles of molecules and these ratios still apply. But since moles and volumes are directly related at constant temperature and pressure, this means we could also describe this reaction in terms of “for each litre” of oxygen gas we consume “two litres of NO” while producing “two litres of NO2”. If we were watching the balloon as this reaction took place, we would see the balloon slowly shrink as, say, a total of three litres of reactant gases get converted into two litres of product gases. Consider this as you attempt the following example.
Example 2
If all gases are measured at the same temperature and pressure, what volume of NH3(g) is produced when 225 L of H2(g) are consumed in the reaction
N2(g) + H2(g) → NH3(g)
not a balanced equation!
SOLUTION
Since balancing the equation shows us that 3 moles of H2 are required to produce 2 moles of NH3, then the law of combining volumes tells us that 3 L of H2 will produce 2 L of NH3. Since we used 225 L of H2 we produced 2/3 (225 L) = 150 L NH3.
Earlier we discussed that if we treat all gases in a mixture as ideal, then by the properties of an ideal gas, none of the gases behave any differently from any of the others, and each gas can be treated separately and the properties of mixture can be treated as a sum of the same properties of the individual gases. This manifests itself as Dalton’s Law of Partial Pressures. The total pressure, Ptot, of a mixture of (ideal) gases is the sum of the pressures of each gas treated individually (partial pressure) at the same temperature and volume as the mixture (Figure 1).
In a mixture of gases A, B, C and D
Equation 1
[latex]P_{\text{tot}} = P_{\text{A}} + P_{\text{B}} + P_{\text{C}} + P_{\text{D}}[/latex]
- [latex]P_{\text{tot}}[/latex], total pressure (variable units) of the system
- [latex]P[/latex], partial pressure (variable units) of gas A, B, C, or D
There are multiple units of pressure, but the unit needs to be consistent in order for the pressures to be additive.
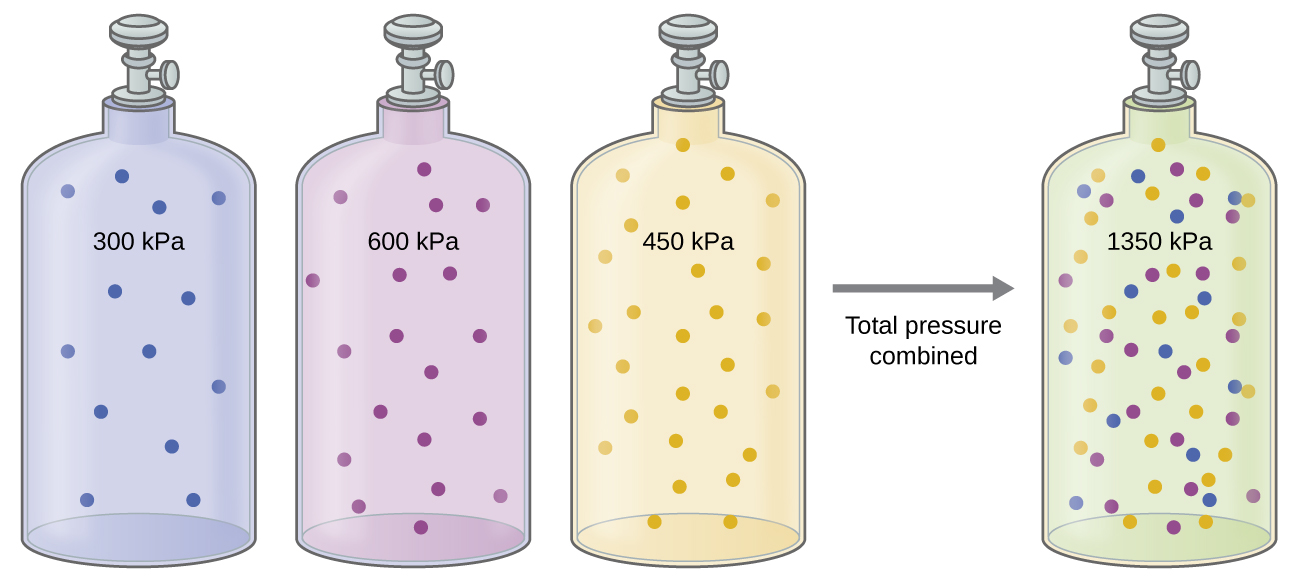
The Law of Combining Volumes directly connects the idea of the relative amount of a gas in a mixture to the volume it is associated with (at constant pressure), while Dalton’s Law connects the relative amount of a gas in a mixture to the partial pressure it is associated with (at constant volume).
Because Dalton’s Law and the Law of Combining Volumes are both intimately associated to the relative amounts of a given gas in a mixture, it makes sense to define a new term for the relative amount of a given gas as compared to the total amount of all gases in a mixture as a fraction or a ratio. The mole fraction of a given component in a mixture is defined as the number of moles of that component divided by the total number of moles of all components in the mixture. Therefore, for a mixture of gases A, B, C, and D, where all the gases are treated ideally, then
ntot = nA + nB + nC + nD
leads to mole fraction of gas A (xA)
Equation 2
[latex]x_{\text{A}} = \dfrac{n_{\text{A}}}{n_{\text{tot}}}[/latex]
- [latex]x_{\text{A}}[/latex], mole fraction of gas A
- [latex]n_{\text{A}}[/latex], moles of gas A
- [latex]n_{\text{tot}}[/latex], total number of moles
With this definition of mole fraction, we see that Dalton’s Law effectively tells us
Equation 3
[latex]P_{\text{A}} = x_{\text{A}}P_{\text{tot}}[/latex]
- [latex]P_{\text{A}}[/latex], partial pressure (variable units) of gas A
- [latex]x_{\text{A}}[/latex], mole fraction of gas A
- [latex]P_{\text{tot}}[/latex], total pressure (variable units) of the system
There are multiple units of pressure, but the unit needs to be consistent for the partial pressure of a gas and the total pressure of the system.
at constant temperature and volume. While the Law of Combining Volumes tells us that
Equation 4
[latex]V_{\text{A}} = x_{\text{A}}V_{\text{tot}}[/latex]
- [latex]V_{\text{A}}[/latex], partial volume (variable units) of gas A
- [latex]x_{\text{A}}[/latex], mole fraction of gas A
- [latex]V_{\text{tot}}[/latex], total volume (variable units) of the system
There are multiple units of volume, but the unit needs to be consistent for the partial volume of a gas and the total volume of the system.
at constant temperature and pressure. In summary, for an ideal gas species A,
Equation 5
[latex]x_{\text{A}} = \dfrac{n_{\text{A}}}{n_{\text{tot}}} = \dfrac{P_{\text{A}}}{P_{\text{tot}}} = \dfrac{V_{\text{A}}}{V_{\text{tot}}}[/latex]
Example 3
What mass of oxygen is in the air contained in a 10 m3 (1000 L = 1 m3) room at 20⁰C and 1.00 atm? Assume the mole fraction of oxygen in the air is 0.20 and that the room contains only air.
SOLUTION
Air at ambient conditions behaves as an ideal gas. Calculate the total moles of gas using the ideal gas law with R = 0.082057 L atm K-1 mol-1
[latex]\begin{eqnarray} PV &=& nRT \\[0.5em] n &=& \frac{PV}{RT} \\[0.5em] &=& \frac{(1.00 \text{ atm})(10 \text{ m}^3)\left(\frac{1000 \text{ L}}{1 \text{ m}^3}\right)}{(0.082057 \text{ L} \cdot \text{atm} \cdot \text{K}^{-1} \cdot \text{mol}^{-1})(20+273.15)\text{K}} \\[0.5em] &=& 4.2\times 10^2 \text{ mol} \end{eqnarray}[/latex]
The moles of oxygen is 0.20 of the total moles of gas
[latex]\begin{eqnarray} x_{\text{O}_2}&=&\frac{n_{\text{O}_2}}{n_{\text{tot}}} \\[0.5em] n_{\text{O}_2}&=&n_{\text{tot}}x_{\text{O}_2} \\[0.5em] &=&\left(4.2\times 10^2 \text{ mol}\right)(0.20) \\[0.5em] &=&83 \text{ mol} \end{eqnarray}[/latex]
Use molar mass to find the mass of oxygen from the moles of oxygen
[latex]m_{\text{O}_2}=(83 \text{ mol})\left(\frac{32.00 \text{ g}}{\text{mol}}\right)=2.7 \times 10^3 \text{ g}=\boxed{2.7 \text{ kg}}[/latex]
Collecting a Sample of Gas Above Water
Another historic chemistry laboratory technique highlights the importance of Dalton’s Law of Partial Pressures, and that is the collecting of gas above water. Sometimes a chemical reaction generates a gas and you want to measure the volume of the gas, ultimately so you can calculate the moles of gas generated. We could capture the gas in a balloon, but the gas may react with the balloon and break it, or measuring the volume of a balloon is not easy in itself if it does not have a consistently round shape.
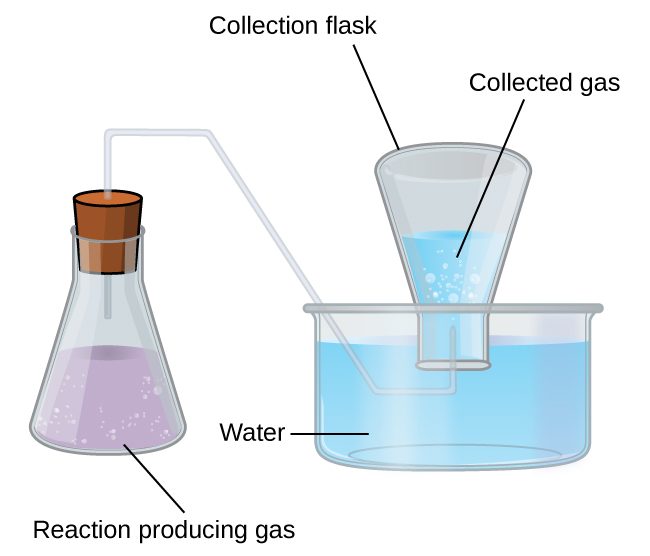
In this case, we can bubble the gas into an inverted tube of water and use the displacement of the water by the gas to determine the actual volume of the gas (Figure 2). However, there is a problem with this. At everyday temperatures, water has the ability to evaporate, and this means that above any body of water, including the water we have collected a gas over, there is some water vapour present in the gas phase. This means that when we collect an unknown gas over water, we do not have a volume of unknown gas, but rather we have a volume of unknown gas that also contains some amount of gaseous water. If we are trying to connect the unknown gas to some reaction stoichiometry, then we have a problem. If we use the ideal gas law to calculate a number of moles of captured gas from the volume of captured gas, this number of moles will include both the unknown gas and the water vapour, which had nothing to do with the reaction that took place. We need to be able to subtract out the contribution from the water vapour to get the true number of moles of unknown gas. To do this, we must rely on a table of vapour pressure of water (Table 1) at given temperatures to tell us exactly how much water we must subtract out from our collected gas at the temperature the experiment took place at.
| Temperature (°C) | Pressure (torr) | Temperature (°C) | Pressure (torr) | Temperature (°C) | Pressure (torr) | ||
|---|---|---|---|---|---|---|---|
| –10 | 1.95 | 18 | 15.5 | 30 | 31.8 | ||
| –5 | 3.0 | 19 | 16.5 | 35 | 42.2 | ||
| –2 | 3.9 | 20 | 17.5 | 40 | 55.3 | ||
| 0 | 4.6 | 21 | 18.7 | 50 | 92.5 | ||
| 2 | 5.3 | 22 | 19.8 | 60 | 149.4 | ||
| 4 | 6.1 | 23 | 21.1 | 70 | 233.7 | ||
| 6 | 7.0 | 24 | 22.4 | 80 | 355.1 | ||
| 8 | 8.0 | 25 | 23.8 | 90 | 525.8 | ||
| 10 | 9.2 | 26 | 25.2 | 95 | 633.9 | ||
| 12 | 10.5 | 27 | 26.7 | 99 | 733.2 | ||
| 14 | 12.0 | 28 | 28.3 | 100.0 | 760.0 | ||
| 16 | 13.6 | 29 | 30.0 | 101.0 | 787.6 | ||
| Table 1 Vapor Pressure of Ice and Water in Various Temperatures at Sea Level. Source: OpenStax Chemistry | |||||||
To assess your understanding of gas mixtures and collecting gas over water and how to correct for it, attempt the following example.
Example 4
The reaction of aluminum with hydrochloric acid produces hydrogen gas
2 Al(s) + 6 HCl(aq) → 2 AlCl3(aq) + 3 H2(g)
If 35.5 mL of H2 is collected over water at 26 ˚C and a barometric pressure of 755 mmHg, how many moles of HCl must have been consumed? The vapour pressure Pwater = 25.2 mmHg at 26 ˚C
SOLUTION
0.00278 moles of HCl consumed
Having trouble figuring out this problem? Consult the following video:
Video 2 Stoichiometry Problem when Collecting Gas over Water (6 min 33 s).
Optional Resource
For more information on Dalton’s Law and collecting a gas over water, read this article.
In an experiment in a laboratory, a sample of hydrogen gas is collected over water at 35.00 degrees Celsius. The measured pressure in the gas container is 783.2 torr. This means the pressure of the hydrogen gas sample is:
A) 741.0 torr
B) 783.2 torr
C) 825.4 torr
Click to see answer
The table of vapour pressure of water indicates that at 35.00°C, the vapour pressure is 42.2 torr. Subtract the vapour pressure of water from the total pressure to find the partial pressure of hydrogen.
[latex]783.2 \text{ torr} – 42.2 \text{ torr} = 741.0 \text{ torr}[/latex]
☆ UNIT 1 ASSIGNMENT
Complete Unit 1 Assignment (graded) on Moodle. This assignment is worth 10% of the course grade.

