Unit 2 Kinetics
2.1 The Rate of a Reaction
OpenStax
Section Learning Objectives
- Define chemical reaction rate.
- Derive relative rate expressions from the balanced equation for a given chemical reaction.
- Calculate reaction rates from experimental data.
- Describe the effects of chemical nature, physical state, concentration, temperature, and catalysis on reaction rates.
✓ SECTION 2.1 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion. | No | 180 min |
| Optional Resource: Watch a video example about reaction rates. | No | 7 min |
| Optional Activity: Play the PhET Reactions & Rates interactive. | No | 23 min |
| Work on the self-check question. | No | 15 min |
| Work on practice exercises. | No | 45 min |
📖 READING PORTION
Expressing the Rate of a Reaction
A rate is a measure of how some property varies with time. Speed is a familiar rate that expresses the distance traveled by an object in a given amount of time. Wage is a rate that represents the amount of money earned by a person working for a given amount of time. Likewise, the rate of a chemical reaction is a measure of how much reactant is consumed, or how much product is produced, by the reaction in a given amount of time.
The rate of reaction is the change in the amount of reactant or product is usually measured as the change in concentration (mol/L or equivalently M) over time (seconds, minutes, hours, etc.). Thus, the units of rate are often expressed as
| mol/(L · s) | mol L−1 s−1 | M/s | M s−1 |
| mol/(L · min) | mol L−1 min−1 | M/min | M min−1 |
| mol/(L · h) | mol L−1 h−1 | M/h | M h−1 |
and so on. Note that the negative exponent on litre, second, minute, and hour means that these units of volume and time belong in the denominator if written as a fraction in the form numerator/denominator. In CHEM 1523, the most common units of reaction rate are of the form concentration per unit time, but there exist other units for quantifying reaction rate. Rates of reactions that consume or produce gaseous substances, for example, are conveniently determined by measuring changes in volume or pressure. For reactions involving one or more coloured substances, rates may be monitored via measurements of light absorption. For reactions involving aqueous electrolytes, rates may be measured via changes in a solution’s conductivity.
Expressing reaction rate as the change in concentration over time is particularly convenient for describing reactants and products in solution. For example, the concentration of hydrogen peroxide, H2O2, in an aqueous solution changes slowly over time as it decomposes according to the equation:
2 H2O2(aq) ⟶ 2 H2O(l) + O2(g)
The rate at which the hydrogen peroxide decomposes can be expressed in terms of the rate of change of its concentration, as shown here:
[latex]\begin{array}{r @{{}={}} l} \text{rate of decomposition of H}_2\text{O}_2 &= \frac{\text{change in concentration of reactant}}{\text{time interval}} \\[0.5em] &= \frac{[\text{H}_2\text{O}_2]_{t_2}\;-\;[\text{H}_2\text{O}_2]_{t_1}}{t_2\;-\;t_1} \\[0.5em] &= \frac{{\Delta}[\text{H}_2\text{O}_2]}{{\Delta}t} \\[0.5em] \text{reaction rate} &= -\frac{1}{2}\frac{{\Delta}[\text{H}_2\text{O}_2]}{{\Delta}t} \end{array}[/latex]
This mathematical representation of the change in species concentration over time is the rate expression for the reaction. The square brackets indicate molar concentrations, and the symbol delta (Δ) indicates “change in.” Thus, [latex][\text{H}_2\text{O}_2]_{t_1}[/latex] represents the molar concentration of hydrogen peroxide at some time t1; likewise,[latex][\text{H}_2\text{O}_2]_{t_2}[/latex] represents the molar concentration of hydrogen peroxide at a later time t2; and Δ[H2O2] represents the change in molar concentration of hydrogen peroxide during the time interval Δt (that is, t2 − t1). Since the reactant concentration decreases as the reaction proceeds, Δ[H2O2] is a negative quantity. The reaction rate is the negative of the expression Δ[H2O2]/Δt because reaction rates are, by convention, positive quantities. The magnitude of the overall reaction rate is the rate Δ[H2O2]/Δt divided by the stoichiometric coefficient. Figure 1 provides an example of data collected during the decomposition of H2O2.
![A table with five columns is shown. The first column is labeled, “Time, h.” Beneath it the numbers 0.00, 6.00, 12.00, 18.00, and 24.00 are listed. The second column is labeled, “[ H subscript 2 O subscript 2 ], mol / L.” Below, the numbers 1.000, 0.500, 0.250, 0.125, and 0.0625 are double spaced. To the right, a third column is labeled, “capital delta [ H subscript 2 O subscript 2 ], mol / L.” Below, the numbers negative 0.500, negative 0.250, negative 0.125, and negative 0.062 are listed such that they are double spaced and offset, beginning one line below the first number listed in the column labeled, “[ H subscript 2 O subscript 2 ], mol / L.” The first two numbers in the second column have line segments extending from their right side to the left side of the first number in the third row. The second and third numbers in the second column have line segments extending from their right side to the left side of the second number in the third row. The third and fourth numbers in the second column have line segments extending from their right side to the left side of the third number in the third row. The fourth and fifth numbers in the second column have line segments extending from their right side to the left side of the fourth number in the third row. The fourth column in labeled, “capital delta t, h.” Below the title, the value 6.00 is listed four times, each single-spaced. The fifth and final column is labeled “Rate of Decomposition, mol / L / h.” Below, the following values are listed single-spaced: negative 0.0833, negative 0.0417, negative 0.0208, and negative 0.0103.](http://principlesofchemistryopencourse.pressbooks.tru.ca/wp-content/uploads/sites/127/2022/08/CNX_Chem_12_01_KDataH2O2.jpg)
To obtain the tabulated results for this decomposition, the concentration of hydrogen peroxide was measured every 6 hours over the course of a day at a constant temperature of 40 °C. Reaction rates were computed for each time interval by dividing the change in concentration by the corresponding time increment, as shown here for the first 6-hour period:
[latex]\frac{{\Delta}[\text{H}_2\text{O}_2]}{{\Delta}t} = \frac{(0.500\;\text{mol/L}\;-\;1.000\;\text{mol/L})}{(6.00\;\text{h}\;-\;0.00\;\text{h})} = -0.0833\;\text{mol L}^{-1}\text{h}^{-1}[/latex]
Notice that the reaction rates vary with time, decreasing as the reaction proceeds. Results for the last 6-hour period yield a reaction rate of:
[latex]\frac{{\Delta}[\text{H}_2\text{O}_2]}{{\Delta}t} = \frac{(0.500\;\text{mol/L}\;-\;1.000\;\text{mol/L})}{(6.00\;\text{h}\;-\;0.00\;\text{h})} = -0.0833\;\text{mol L}^{-1}\text{h}^{-1}[/latex]
[latex]\frac{{\Delta}[\text{H}_2\text{O}_2]}{{\Delta}t} = \frac{(0.0625\;\text{mol/L}\;-\;0.125\;\text{mol/L})}{(24.00\;\text{h}\;-\;18.00\;\text{h})} = -0.0104\;\text{mol L}^{-1}\text{h}^{-1}[/latex]
This behavior indicates the reaction continually slows with time. Using the concentrations at the beginning and end of a time period over which the reaction rate is changing results in the calculation of an average rate for the reaction over this time interval. At any specific time, the rate at which a reaction is proceeding is known as its instantaneous rate. The instantaneous rate of a reaction at “time zero,” when the reaction commences, is its initial rate. Consider the analogy of a car slowing down as it approaches a stop sign. The vehicle’s initial rate—analogous to the beginning of a chemical reaction—would be the speedometer reading at the moment the driver begins pressing the brakes (t0). A few moments later, the instantaneous rate at a specific moment—call it t1—would be somewhat slower, as indicated by the speedometer reading at that point in time. As time passes, the instantaneous rate will continue to fall until it reaches zero, when the car (or reaction) stops. Unlike instantaneous speed, the car’s average speed is not indicated by the speedometer; but it can be calculated as the ratio of the distance traveled to the time required to bring the vehicle to a complete stop (Δt). Like the decelerating car, the average rate of a chemical reaction will fall somewhere between its initial and final rates.
The instantaneous rate of a reaction may be determined one of two ways. If experimental conditions permit the measurement of concentration changes over very short time intervals, then average rates computed as described earlier provide reasonably good approximations of instantaneous rates. Alternatively, a graphical procedure may be used that, in effect, yields the results that would be obtained if short time interval measurements were possible. If we plot the concentration of hydrogen peroxide against time, the instantaneous rate of decomposition of H2O2 at any time t is given by the slope of a straight line that is tangent to the curve at that time (Figure 2). We can use calculus to evaluating the slopes of such tangent lines, but the procedure for doing so is beyond the scope of this course.
![A graph is shown with the label, “Time ( h ),” appearing on the x-axis and “[ H subscript 2 O subscript 2 ] ( mol L superscript negative 1)” on the y-axis. The x-axis markings begin at 0 and end at 24. The markings are labeled at intervals of 6. The y-axis begins at 0 and includes markings every 0.200, up to 1.000. A decreasing, concave up, non-linear curve is shown, which begins at 1.000 on the y-axis and nearly reaches a value of 0 at the far right of the graph around 10 on the x-axis. A red tangent line segment is drawn on the graph at the point where the graph intersects the y-axis. A second red tangent line segment is drawn near the middle of the curve. A vertical dashed line segment extends from the left endpoint of the line segment downward to intersect with a similar horizontal line segment drawn from the right endpoint of the line segment, forming a right triangle beneath the curve. The vertical leg of the triangle is labeled “capital delta [ H subscript 2 O subscript 2 ]” and the horizontal leg is labeled, “capital delta t.”](http://principlesofchemistryopencourse.pressbooks.tru.ca/wp-content/uploads/sites/127/2022/10/CNX_Chem_12_01_RRateIll.jpg)
Relative Reaction Rates
We saw above that the rate of consumption of H2O2 is the change in H2O2 concentration over time, Δ[H2O2]/Δt . We are able to use the equation stoichiometry to relate the rate of one reactant to that of any other reactants, products, and the overall rate of the reaction as follows:

We make several observations about the expression for relative reaction rates:
- The overall rate of reaction is equal to the rate for individual species (for example, Δ[A]/Δt) divided by the stoichiometric coefficient of the species.
- The rates for reactants (here, A and B) are multiplied by a negative sign to ensure positive quantities even though the concentrations of A and B are decreasing as the reaction progresses. The plus signs for the rates of products C and D are not necessary but included to make an explicit distinction from reactants.
- The rate for one species can be solved algebraically using the rate of another species.
Consider the reaction
2 NH3(g) ⟶ N2(g) + 3 H2(g)
The relationship between the reaction rates can be expressed as
[latex]\text{rate} = -\frac{1}{2}\frac{\Delta [\text{NH}_3]}{\Delta t} = \frac{\Delta [\text{N}_2]}{\Delta t} = \frac{1}{3}\frac{\Delta [\text{H}_2]}{\Delta t}[/latex]
If we know the rate of nitrogen production, we can solve for the rate of ammonia consumption by comparing the appropriate quantities
[latex]-\frac{1}{2}\frac{\Delta [\text{NH}_3]}{\Delta t} = \frac{\Delta [\text{N}_2]}{\Delta t}[/latex]
[latex]\frac{\Delta [\text{NH}_3]}{\Delta t} = -2 \frac{\Delta [\text{N}_2]}{\Delta t}[/latex]
The rate of change of ammonia concentration is in the opposite direction (difference in sign) and twice that of nitrogen concentration. This result makes sense because the negative sign specific to ammonia indicates that reactant concentration is decreasing, and the stoichiometry shows that two moles of ammonia is used to produce one mole of nitrogen. We can also see from the relative rate expression
[latex]\frac{\Delta [\text{N}_2]}{\Delta t} = \frac{1}{3}\frac{\Delta [\text{H}_2]}{\Delta t}[/latex]
[latex]\frac{\Delta [\text{H}_2]}{\Delta t} = 3 \frac{\Delta [\text{N}_2]}{\Delta t}[/latex]
meaning that hydrogen is produced at three times faster rate than nitrogen, in agreement with the reaction stoichiometry where 3 moles of hydrogen are produced for each mole of nitrogen.
Example 1
Expressions for Relative Reaction Rates
The first step in the production of nitric acid is the combustion of ammonia
4 NH3(g) + 5 O2(g) ⟶ 4 NO(g) + 6 H2O(g)
Write the equations that relate the rates of consumption of the reactants and the rates of formation of the products.
SOLUTION
Considering the stoichiometry of this homogeneous reaction, the rates for the consumption of reactants and formation of products are
[latex]\text{rate} = -\frac{1}{4}\frac{\Delta [\text{NH}_3]}{\Delta t} = -\frac{1}{5}\frac{\Delta [\text{O}_2]}{\Delta t} = \frac{1}{4}\frac{\Delta [\text{NO}]}{\Delta t}= \frac{1}{6}\frac{\Delta [\text{H}_2\text{O}]}{\Delta t}[/latex]
Example 2
Reaction Rate Expressions for Decomposition of H2O2
The decomposition of hydrogen peroxide into water and oxygen is
2 H2O2(aq) ⟶ 2 H2O(l) + O2(g)
The concentration of hydrogen peroxide decreased from 0.250 to 0.125 mol/L over the time interval of 6.00 h. What is the rate of production of water and oxygen and the overall rate of reaction?
SOLUTION
The rate of decomposition of H2O2 is
Δ[H2O2]/Δt = (0.125 – 0.250)mol/L / 6.00 h = −0.0208 mol/(L · h)
The rates of each species and the overall rate of reaction is expressed as
[latex]\text{rate} = -\frac{1}{2}\frac{\Delta [\text{H}_2\text{O}_2]}{\Delta t} = \frac{1}{2}\frac{\Delta [\text{H}_2\text{O}]}{\Delta t} = \frac{\Delta [\text{O}_2]}{\Delta t}[/latex]
We see that
[latex]-\frac{1}{2}\frac{\Delta [\text{H}_2\text{O}_2]}{\Delta t} = \frac{1}{2}\frac{\Delta [\text{H}_2\text{O}]}{\Delta t}[/latex]
Solve explicitly for Δ[H2O]/Δt and substitute in the numerical value,
[latex]\frac{\Delta [\text{H}_2\text{O}]}{\Delta t} = -\frac{\Delta [\text{H}_2\text{O}_2]}{\Delta t} = 0.0208 \text{ mol/(L }\cdot\text{ h)}[/latex]
Similarly, for oxygen,
[latex]\frac{\Delta [\text{O}_2]}{\Delta t} = -\frac{1}{2}\frac{\Delta [\text{H}_2\text{O}_2]}{\Delta t} = \frac{1}{2}(0.0208 \text{ mol/(L }\cdot \text{ h)}) = 0.0104 \text{ mol/(L }\cdot \text{ h)}[/latex]
The overall rate of reaction is
[latex]\text{rate} = -\frac{1}{2}\frac{\Delta [\text{H}_2\text{O}_2]}{\Delta t}=\frac{1}{2}(0.0208 \text{ mol/(L }\cdot \text{ h)})=0.0104 \text{ mol/(L }\cdot \text{ h)}[/latex]
Factors Affecting Reaction Rates
The rates at which reactants are consumed and products are formed during chemical reactions vary greatly. Five factors typically affecting the rates of chemical reactions will be explored in this section: the chemical nature of the reacting substances, the surface area of any solid reactants (one large solid clump versus fine powder), the concentration of the reactants, the temperature of the reactants, and the presence of a catalyst.
The Chemical Nature of the Reacting Substances
The rate of a reaction depends on the nature of the participating substances. Some species are more reactive than others. Reactions that appear similar may have different rates under the same conditions, depending on the identity of the reactants. For example, when small pieces of the metals iron and sodium are exposed to air, the sodium reacts completely with air overnight, whereas the iron is barely affected. The active metals calcium and sodium both react with water to form hydrogen gas and a base. Yet calcium reacts at a moderate rate, whereas sodium reacts so rapidly that the reaction is almost explosive.
The Physical States of the Reactants
A chemical reaction between two or more substances requires intimate contact between the reactants. When reactants are in different physical states, or phases (solid, liquid, gaseous, dissolved), the reaction takes place only at the interface between the phases. Consider the heterogeneous reaction between a solid phase and either a liquid or gaseous phase. Compared with the reaction rate for large solid particles, the rate for smaller particles will be greater because the surface area in contact with the other reactant phase is greater. For example, large pieces of iron react more slowly with acids than they do with finely divided iron powder (Figure 3). Large pieces of wood smolder, smaller pieces burn rapidly, and saw dust burns explosively. Watch Video 1 to see the reaction of calcium carbonate with hydrochloric acid and a discussion of how the state of reactants and particle size affect reaction rates.
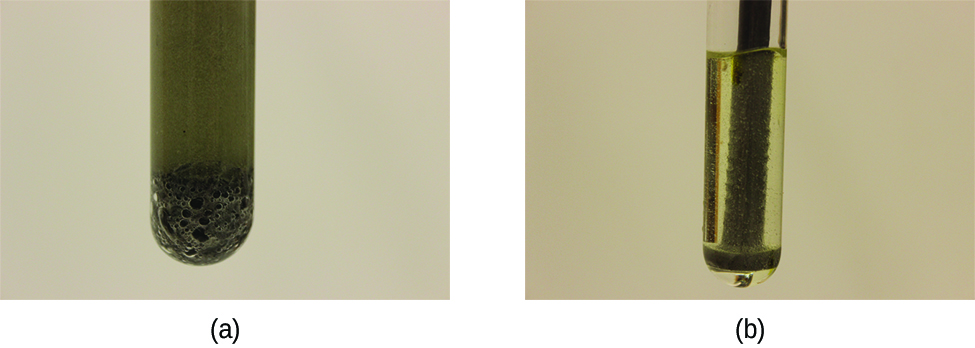
Video 1 Effect of Particle Size on reaction rates (3 min 12 s).
Concentrations of the Reactants
The rates of many reactions depend on the concentrations of the reactants. Rates usually increase when the concentration of one or more of the reactants increases. For example, sculptures made of limestone (calcium carbonate, CaCO3) deteriorates as a result of its reaction with the pollutant sulfur dioxide in acid rain. The rate of this reaction depends on the amount of sulfur dioxide in the air. In a polluted atmosphere where the concentration of sulfur dioxide is high, calcium carbonate deteriorates more rapidly than in less polluted air. Similarly, phosphorus burns much more rapidly in an atmosphere of pure oxygen than in air, which is only about 20% oxygen. Watch Video 2 to see how phosphorus burns rapidly in air, but it will burn even more rapidly if the concentration of oxygen is higher. The effect of concentration on reaction rate will be discussed in further detail in Section 2.2.
Video 2 All about White Phosphorus | Element Series (3 min 2 s).
![]()
Do not do dangerous experiments without appropriate supervision and/or permission.
Temperature of the Reactants
Chemical reactions typically occur faster at higher temperatures. Food can spoil quickly when left on the kitchen counter. However, the lower temperature inside of a refrigerator slows that process so that the same food remains fresh for days. Gas burners, hot plates, and ovens are often used in the laboratory to increase the speed of reactions that proceed slowly at ordinary temperatures. For many chemical processes, reaction rates are approximately doubled when the temperature is raised by 10°C. The effect of temperature on the reaction rate will be discussed in further detail in Section 2.4.
The Presence of a Catalyst
Relatively dilute aqueous solutions of hydrogen peroxide, H2O2, are commonly used as topical antiseptics. Hydrogen peroxide decomposes to yield water and oxygen gas according to the equation:
2 H2O2(aq) ⟶ 2 H2O(l) + O2(g)
Under typical conditions, this decomposition occurs very slowly. When dilute H2O2(aq) is poured onto an open wound, however, the reaction occurs rapidly and the solution foams because of the vigorous production of oxygen gas. This dramatic difference is caused by the presence of substances within the wound’s exposed tissues that accelerate the decomposition process. Substances that function to increase the rate of a reaction are called catalysts. Catalysis will be discussed in further detail in Section 2.6.
Optional Resource
Watch a video example about reaction rates.
Video 3 Intro to Rate Laws (6 min 45 s).
Optional Activity
PhET Reactions & Rates Interactive
Chemical reactions occur when molecules collide with each other and undergo a chemical transformation. Before physically performing a reaction in a laboratory, scientists can use molecular modeling simulations to predict how the parameters discussed earlier will influence the rate of a reaction. Use the PhET Reactions & Rates interactive to explore how temperature, concentration, and the nature of the reactants affect reaction rates.
Which of the following may have an effect on reaction rate?
A) Temperature
B) Concentration of reactants
C) Surface area of solid reactants
D) All of the above
Click to see answer
D) All of the above

