Unit 3 Equilibrium
3.3 The Equilibrium Quotient and Constant
OpenStax
Section Learning Objectives
- Derive reaction quotients from chemical equations representing homogeneous and heterogeneous reactions.
- Calculate values of reaction quotients and equilibrium constants.
- Relate the magnitude of an equilibrium constant to the extent of reaction of the chemical system.
✓ SECTION 3.3 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion. | No | 60 min |
| Optional Resource: Watch a video explanation of equilibrium constant expressions. |
No | 32 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 60 min |
📖 READING PORTION
The Equilibrium Quotient
In Section 3.1, we saw that for a system in equilibrium, the concentrations of reactants and products are constant. However, stresses on the equilibrium cause the equilibrium to shift left or right, Section 3.2. Here, we use numbers to describe the relative amounts of reactant and product at equilibrium and predict the shift due to stresses on the equilibrium.
The status of a reversible reaction is conveniently assessed by a quantity called the reaction quotient (Q ). For a reversible reaction described by
a A + b B ⇌ c C + d D
the reaction quotient is derived directly from the stoichiometry of the balanced equation as
[latex]Q_\text{c} = \frac{[\text{C}]^c[\text{D}]^d}{[\text{A}]^a[\text{B}]^b}[/latex]
where the subscript c on Q denotes the use of molar concentrations in the expression. If the reactants and products are gaseous, a reaction quotient may be similarly derived using partial pressures
[latex]Q_\text{p} = \frac{P_\text{C}^c\;P_\text{D}^d}{P_\text{A}^a\;P_\text{B}^b}[/latex]
A heterogeneous equilibrium involves reactants and products in two or more different phases, as illustrated by the following examples in Table 1. The reaction quotient expression does not include solid species or pure liquids because the concentration of these substances does not change. Liquid species that are solvents, such as water in an aqueous reaction, are excluded from the reaction quotient expression because the amount of liquid is present in a great quantity such that the reaction does not affect the amount of the solvent to a large extent. Concentration terms are only included for gaseous and solute species.
|
Equation |
Qc |
Qp |
|
PbCl2(s) ⇌ Pb2+(aq) + 2 Cl−(aq) |
Qc = [Pb2+][Cl−]2 |
— |
|
CaO(s) + CO2(g) ⇌ CaCO3(s) |
Qc = 1/[CO2] |
Qp = 1/PCO2 |
|
C(s) + 2 S(g) ⇌ CS2(g) |
Qc = [CS2]/[S]2 |
Qp = PCS2 / PS2 |
|
Br2(l) ⇌ Br2(g) |
Qc = [Br2(g)] |
Qp = PBr2 |
|
CH3COOH(aq) + H2O(l) ⇌ CH3COO−(aq) + H3O+(aq) |
Qc = [CH3COO−][H3O+]/[CH3COOH] |
— |
|
Table 1 Examples of equilibrium quotient expressions. |
||
Note that the reaction quotient equations above are a simplification of more rigorous expressions that use relative values for concentrations and pressures rather than absolute values. These relative concentration and pressure values are dimensionless (they have no units); consequently, so are the reaction quotients. For purposes of this introductory text, it will suffice to use the simplified equations and to disregard units when computing Q. In most cases, this will introduce only modest errors in calculations involving reaction quotients.
Example 1
Writing Reaction Quotient Expressions
Write the concentration- and partial pressure-based reaction quotient expression for each of the following reactions:
(a) ClNO2(g) + NO(g) ⇌ NO2(g) + ClNO(g)
(b) 3 O2(g) ⇌ 2 O3(g)
(c) N2(g) + 3 H2(g) ⇌ 2 NH3(g)
(d) 4 NH3(g) + 7 O2(g) ⇌ 4 NO2(g) + 6 H2O(g)
SOLUTION
(a) [latex]Q_\text{c} = \frac{[\text{NO}_2][\text{ClNO}]}{[\text{ClNO}_2][\text{NO}]}[/latex], [latex]Q_\text{p} = \frac{P_{\text{NO}_2}P_{\text{ClNO}}}{P_{\text{ClNO}_2}P_{\text{NO}}}[/latex]
(b) [latex]Q_\text{c} = \frac{[\text{O}_3]^2}{[\text{O}_2]^3}[/latex], [latex]Q_\text{p} = \frac{P_{\text{O}_3}^2}{P_{\text{O}_2}^3}[/latex]
(c) [latex]Q_\text{c} = \frac{[\text{NH}_3]^2}{[\text{N}_2][\text{H}_2]^3}[/latex], [latex]Q_\text{p} = \frac{P_{\text{NH}_3}^2}{P_{\text{N}_2}P_{\text{H}_2}^3}[/latex]
(d) [latex]Q_\text{c} = \frac{[\text{NO}_2]^4[\text{H}_2\text{O}]^6}{[\text{NH}_3]^4[\text{O}_2]^7}[/latex], [latex]Q_\text{p} = \frac{P_{\text{NO}_2}^4 P_{\text{H}_2\text{O}}^6}{P_{\text{NH}_3}^4P_{\text{O}_2}^7}[/latex]
The numerical value of Q varies as a reaction proceeds towards equilibrium; therefore, it can serve as a useful indicator of the reaction’s status. To illustrate this point, consider the oxidation of sulfur dioxide
2 SO2(g) + O2(g) ⇌ 2 SO3(g)
Two different experimental scenarios are depicted in Figure 1, one in which this reaction is initiated with a mixture of reactants only, SO2 and O2, and another that begins with only product, SO3. For the reaction that begins with a mixture of reactants only, Q is initially equal to zero
[latex]Q_\text{c} = \frac{[\text{SO}_3]^2}{[\text{SO}_2]^2[\text{O}_2]} = \frac{0^2}{[\text{SO}_2]^2[\text{O}_2]} = 0[/latex]
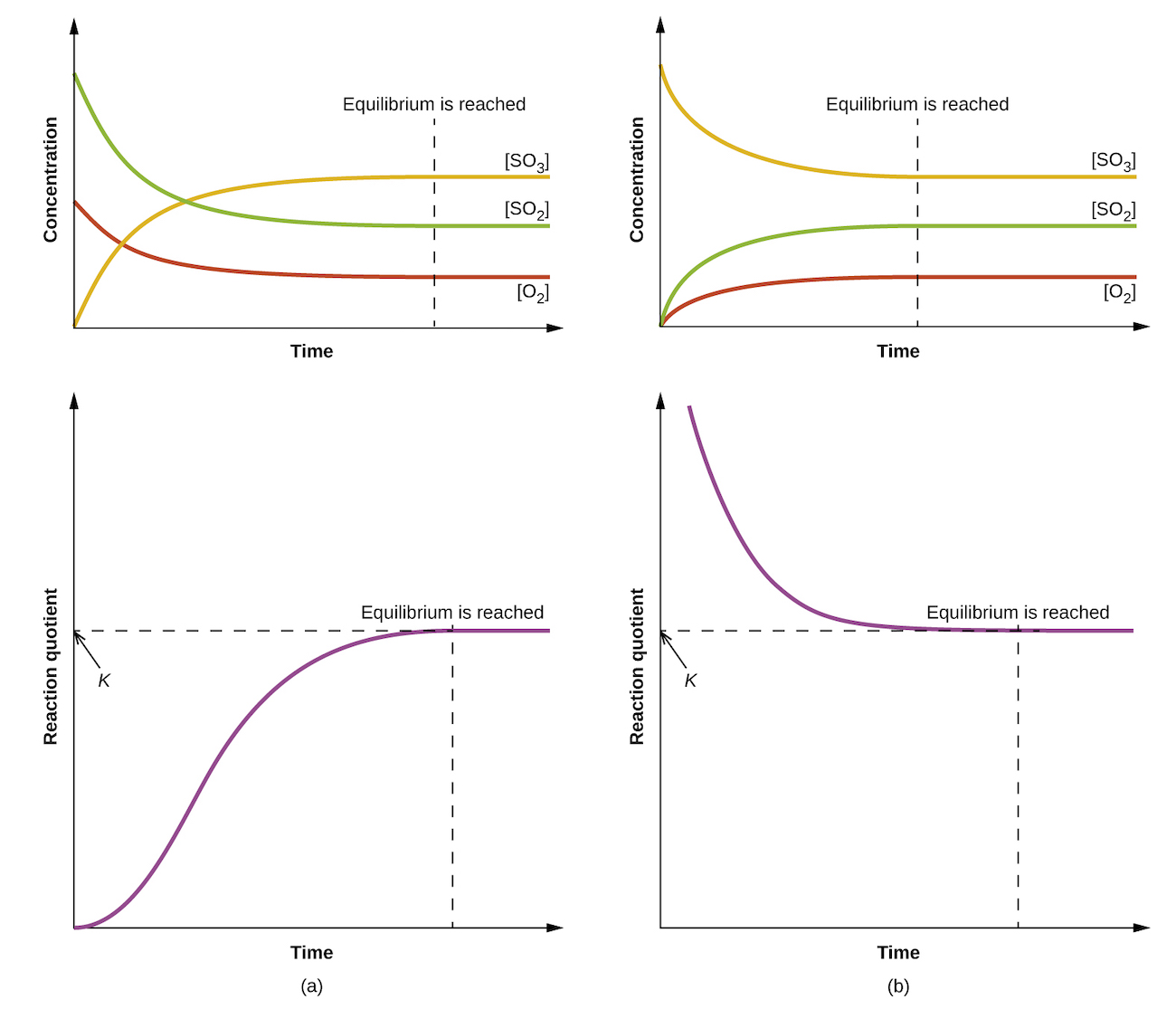
As the reaction proceeds toward equilibrium in the forward direction, reactant concentrations decrease (as does the denominator of Qc), product concentration increases (as does the numerator of Qc), and the reaction quotient consequently increases. When equilibrium is achieved, the concentrations of reactants and product remain constant, as does the value of Qc.
If the reaction begins with only product present, the value of Qc is initially undefined (immeasurably large, or infinite)
[latex]Q_\text{c} = \frac{[\text{SO}_3]^2}{[\text{SO}_2]^2 [\text{O}_2]} = \frac{[\text{SO}_3]^2}{0} → ∞[/latex]
In this case, the reaction proceeds toward equilibrium in the reverse direction. The product concentration and the numerator of Qc decrease with time, the reactant concentrations and the denominator of Qc increase, and the reaction quotient consequently decreases until it becomes constant at equilibrium.
The constant value of Q exhibited by a system at equilibrium is called the equilibrium constant (K )
K ≡ Q at equilibrium
Comparison of the data plots in Figure 1 shows that both experimental scenarios resulted in the same value for the equilibrium constant. This is a general observation for all equilibrium systems, known as the law of mass action: At a given temperature, the reaction quotient for a system at equilibrium is constant.
Example 2
Evaluating a Reaction Quotient
Gaseous nitrogen dioxide forms dinitrogen tetroxide according to this equation
2 NO2(g) ⇌ N2O4(g)
When 0.10 mol NO2 is added to a 1.0-L flask at 25°C, the concentration changes so that at equilibrium, [NO2] = 0.016 M and [N2O4] = 0.042 M.
(a) What is the value of the reaction quotient before any reaction occurs?
(b) What is the value of the equilibrium constant for the reaction?
SOLUTION
As for all equilibrium calculations in this text, use the simplified equations for Q and K and disregard any concentration or pressure units.
(a) Before any product is formed, [NO2] = 0.10 mol / 1.0 L = 0.10 M, and [N2O4] = 0 M. Thus,
Qc = [N2O4] / [NO2]2 = 0 / 0.102 = 0
(b) At equilibrium, Kc = Qc = [N2O4]/[NO2]2 = 0.042/0.0162 = 1.6 × 102.
The equilibrium constant is 1.6 × 102.
![]()
The values of partial pressures are in atm for Qp and Kp. Technically, the partial pressures in Qp and Kp are relative to the standard pressure (1 bar), but this technique is beyond the scope of this course.
The Extent of a Reaction
By its definition, the magnitude of an equilibrium constant explicitly reflects the composition of a reaction mixture at equilibrium, and it may be interpreted with regard to the extent of the forward reaction. A reaction exhibiting a large K will reach equilibrium when most of the reactant has been converted to product, whereas a small K indicates the reaction achieves equilibrium after very little reactant has been converted. It’s important to keep in mind that the magnitude of K does not indicate how rapidly or slowly equilibrium will be reached. Some equilibria are established so quickly as to be nearly instantaneous, and others so slowly that no perceptible change is observed over the course of days, years, or longer.
The equilibrium constant for a reaction can be used to predict the behaviour of mixtures containing its reactants and/or products. As demonstrated by the sulfur dioxide oxidation process described above, a chemical reaction will proceed in whatever direction is necessary to achieve equilibrium. Comparing Q to K for an equilibrium system of interest allows prediction of what reaction (forward or reverse), if any, will occur.
To further illustrate this important point, consider the reversible reaction shown below:
CO(g) + H2O(g) ⇌ CO2(g) + H2(g) Kc = 0.640 T = 800°C
The bar charts in Figure 2 represent changes in reactant and product concentrations for three different reaction mixtures. The reaction quotients for mixtures 1 and 3 are initially lesser than the reaction’s equilibrium constant, so each of these mixtures will experience a net forward reaction to achieve equilibrium. The reaction quotient for mixture 2 is initially greater than the equilibrium constant, so this mixture will proceed in the reverse direction until equilibrium is established.

Example 3
Predicting the Direction of Reaction
Given here are the starting concentrations of reactants and products for three experiments involving this reaction
CO(g) + H2O(g) ⇌ CO2(g) + H2(g) Kc = 0.64
Determine in which direction the reaction proceeds as it goes to equilibrium in each of the three experiments shown.
| Reactants or Products | Experiment 1 | Experiment 2 | Experiment 3 |
| [CO] | 0.020 M | 0.011 M | 0.0094 M |
| [H2O] | 0.020 M | 0.0011 M | 0.0025 M |
| [CO2] | 0.0040 M | 0.037 M | 0.0015 M |
| [H2] | 0.0040 M | 0.046 M | 0.0076 M |
SOLUTION
Experiment 1:
[latex]Q_\text{c} = \frac{[\text{CO}_2][\text{H}_2]}{[\text{CO}][\text{H}_2\text{O}]} = \frac{(0.0040)(0.0040)}{(0.020)(0.020)} = 0.040[/latex]
Qc < Kc (0.040 < 0.64)
The reaction will proceed in the forward direction.
Experiment 2:
[latex]Q_\text{c} = \frac{[\text{CO}_2][\text{H}_2]}{[\text{CO}][\text{H}_2\text{O}]} = \frac{(0.037)(0.046)}{(0.011)(0.0011)} = 1.4×10^2[/latex]
Qc > Kc (140 > 0.64)
The reaction will proceed in the reverse direction.
Experiment 3:
[latex]Q_\text{c} = \frac{[\text{CO}_2][\text{H}_2]}{[\text{CO}][\text{H}_2\text{O}]} = \frac{(0.0015)(0.0076)}{(0.0094)(0.0025)} = 0.48[/latex]
Qc < Kc (0.48 < 0.64)
The reaction will proceed in the forward direction.
The Value of the Equilibrium Constant Varies with Temperature
There are several stresses that could be exerted on an equilibrium, such as changes to the system volume and the concentrations and partial pressures of reactants and products. These stresses do not affect the value of the equilibrium constant. However, changes to temperature can, in fact, alter the value of the equilibrium constant. For an endothermic reaction, raising the temperature increases the equilibrium constant, and lowering the temperature decreases the equilibrium constant. The opposite is true for exothermic reactions, where the equilibrium constant decreases with increased temperature and increases with decreased temperature. It is advisable to state the temperature when reporting equilibrium constants.
Coupled Equilibria
The equilibrium systems discussed so far have all been relatively simple, involving just single reversible reactions. Many systems, however, involve two or more coupled equilibrium reactions, those which have in common one or more reactant or product species. Since the law of mass action allows for a straightforward derivation of equilibrium constant expressions from balanced chemical equations, the K value for a system involving coupled equilibria can be related to the K values of the individual reactions. Three basic manipulations are involved in this approach.
- Changing the direction of a chemical equation essentially swaps the identities of “reactants” and “products,” and so the equilibrium constant for the reversed equation is simply the reciprocal of that for the forward equation.
[latex]\begin{align*} \text{reaction 1:}&&\;\text{A}\;&{\rightleftharpoons}\;\text{B} && K_{\text{c}1} = \frac{[\text{B}]}{[\text{A}]}\\ \\ \text{reaction 2:}&&\;\text{B}\;&{\rightleftharpoons}\;\text{A} && K_{\text{c}2}=\frac{[\text{A}]}{[\text{B}]} \end{align*}[/latex]
[latex]K_{\text{c}1} = \frac{1}{K_{\text{c}2}}[/latex]
- Multiplying the stoichiometric coefficients in an equation by some factor n results in an exponential change in the equilibrium constant by that same factor.
[latex]\begin{align*} \text{reaction 1:}&&\;\text{A}\;&{\rightleftharpoons}\;\text{B} && K_{\text{c}1} = \frac{[\text{B}]}{[\text{A}]}\\ \\ \text{reaction 3:}&&\;n\text{ A}\;&{\rightleftharpoons}\;n \text{ B} && K_{\text{c}3}=\frac{[\text{B}]^n}{[\text{A}]^n} \end{align*}[/latex]
[latex]K_{\text{c}3}= (K_{\text{c}1})^n[/latex]
- Adding two or more equilibrium equations together yields an overall equation whose equilibrium constant is the mathematical product of the individual reaction’s K values. The net reaction for these coupled equilibria is obtained by summing the two equilibrium equations and cancelling any redundancies.
[latex]\begin{align*} \text{reaction 1:}&&\;\text{A}\;&{\rightleftharpoons}\;\text{B} && K_{\text{c}1} = \frac{[\text{B}]}{[\text{A}]}\\ \\ \text{reaction 4:}&&\;\text{B}\;&{\rightleftharpoons}\;\text{C} && K_{\text{c}4}=\frac{[\text{C}]}{[\text{B}]} \\ \\ \hline \\ \text{overall:}&&\;\text{A}\;&{\rightleftharpoons}\;\text{C} && K_{\text{c, overall}} = \frac{[\text{C}]}{[\text{A}]}=K_{\text{c1}}K_{\text{c4}} \end{align*}[/latex]
Example 4
Equilibrium Constant for Coupled Reactions
A mixture containing nitrogen, hydrogen, and iodine established the following equilibrium at 400 °C:
2 NH3(g) + 3 I2(g) ⇌ N2(g) + 6 HI(g)
Use the information below to calculate Kc for this reaction.
[latex]\begin{align*} \text{N}_2(g)\;+\;3\text{ H}_2(g)\;&{\rightleftharpoons}\;2\text{ NH}_3(g) && K_{\text{c}1} = 0.50 \text{ at } 400^\circ\text{C}\\ \text{H}_2(g)\;+\;\text{I}_2(g)\;&{\rightleftharpoons}\;2\text{ HI}(g) && K_{\text{c}2} = 50 \text{ at } 400^\circ\text{C}\\ \end{align*}[/latex]
SOLUTION
The equilibrium equation of interest and its K value may be derived from the equations for the two coupled reactions as follows.
Reverse the first reaction equation:
[latex]\begin{align*} 2\text{ NH}_3(g)\;&{\rightleftharpoons}\;\text{N}_2(g)\;+\;3\text{ H}_2(g) && \frac{1}{K_{\text{c}1}} = \frac{1}{0.50} \end{align*}[/latex]
Multiply the second reaction by 3:
[latex]\begin{align*} 3\text{ H}_2(g)\;+\;3\text{ I}_2(g)\;&{\rightleftharpoons}\;6\text{ HI}(g) && (K_{\text{c}2})^3 = (50)^3 \end{align*}[/latex]
Finally, add the two revised equations:
[latex]\begin{align*} 2\text{ NH}_3(g)\;&{\rightleftharpoons}\;\text{N}_2(g)\;+\;3\text{ H}_2(g) && \frac{1}{K_{\text{c}1}} = \frac{1}{0.50} \\ 3\text{ H}_2(g)\;+\;3\text{ I}_2(g)\;&{\rightleftharpoons}\;6\text{ HI}(g) && (K_{\text{c}2})^3 = (50)^3 \\ \\ \hline \\ 2\text{ NH}_3(g)\;+\;3\text{ I}_2(g)\;&{\rightleftharpoons}\;\text{N}_2(g)\;+\;6\text{ HI}(g) \end{align*}[/latex]
[latex]K_{\text{c, overall}} = \frac{1}{K_{\text{c}1}}(K_{\text{c}2})^3 = \frac{1}{0.50}(50)^3=\boxed{2.5\times10^5}[/latex]
Optional Resource
Watch a video explanation on equilibrium constant expressions.
Video 1 CHM175 More Equilibrium Constant Expression Tips (31 min 58 s).
Which of the following statements is correct?
A) When K >> 1, the reverse reaction is favored and essentially goes to completion.
B) K >> 1 implies that the reaction is very fast at producing products.
C) When K << 1, the forward reaction is favored, and the reverse reaction does not proceed to a great extent.
D) K << 1 implies that the reaction is very slow at producing products.
E) When K ≈ 1, neither the forward nor reverse reaction is strongly favored, and about the same concentrations of reactants and products exist at equilibrium.
Click to see answer
E) When K ≈ 1, neither the forward nor reverse reaction is strongly favored, and about the same concentrations of reactants and products exist at equilibrium.

