Unit 3 Equilibrium

3.4 Equilibrium Calculations

OpenStax

Section Learning Objectives

  • Identify the changes in concentration that occur for chemical species in equilibrium systems.
  • Calculate equilibrium concentrations and equilibrium constants, using various algebraic approaches.

✓ SECTION 3.4 CHECKLIST

Learning Activity Graded? Estimated Time
Make notes about this section’s reading portion. No 90 min
Optional Resources: Watch the suggested videos. No 26 min
Work on the self-check question. No 10 min
Work on practice exercises. No 190 min
Complete Unit 3 Assignment on Moodle. Yes 90 min

📖 READING PORTION
Having covered the essential concepts of chemical equilibria in the preceding sections of this unit, here we will demonstrate the more practical aspect of using these concepts and appropriate mathematical strategies to perform various equilibrium calculations. These types of computations are essential to many areas of science and technology—for example, in the formulation and dosing of pharmaceutical products. After a drug is ingested or injected, it is typically involved in several chemical equilibria that affect its ultimate concentration in the body system of interest. Knowledge of the quantitative aspects of these equilibria is required to compute a dosage amount that will solicit the desired therapeutic effect.

Many of the useful equilibrium calculations that will be demonstrated here require terms representing changes in reactant and product concentrations. These terms are derived from the stoichiometry of the reaction, as illustrated by decomposition of ammonia

[latex]2\text{ NH}_3(g)\;{\rightleftharpoons}\;\text{N}_2(g)\;+\;3\text{ H}_2(g)[/latex]

As shown earlier in this unit, this equilibrium may be established within a sealed container that initially contains either NH3 only, or a mixture of any two of the three chemical species involved in the equilibrium. Regardless of its initial composition, a reaction mixture will show the same relationships between changes in the concentrations of the three species involved, as dictated by the reaction stoichiometry. For example, if the nitrogen concentration increases by an amount x

Δ[N2] = + x

the corresponding changes in the other species concentrations are

Δ[H2] = + 3x

Δ[NH3] = − 2x

where the negative sign indicates a decrease in concentration.

Because the value of the reaction quotient of any reaction at equilibrium is equal to its equilibrium constant, we can use the mathematical expression for Qc (i.e., the law of mass action) to determine a number of quantities associated with a reaction at equilibrium. It may help if we keep in mind that Qc = Kc (at equilibrium) in all of these situations and that there are only three basic types of calculations:

  1. Calculation of an equilibrium constant. If concentrations of reactants and products at equilibrium are known, the value of the equilibrium constant for the reaction can be calculated.
  2. Calculation of missing equilibrium concentrations. If the value of the equilibrium constant and all of the equilibrium concentrations, except one, are known, the remaining concentration can be calculated.
  3. Calculation of equilibrium concentrations from initial concentrations. If the value of the equilibrium constant and a set of concentrations of reactants and products that are not at equilibrium are known, the concentrations at equilibrium can be calculated.

Calculation of an Equilibrium Constant

The equilibrium constant for a reaction is calculated from the equilibrium concentrations of its reactants and products. If these concentrations are known, the calculation simply involves their substitution into the K expression. A slightly more challenging example is provided next, in which the reaction stoichiometry is used to derive equilibrium concentrations from the information provided. The basic strategy of this computation is helpful for many types of equilibrium computations and relies on the use of terms for the reactant and product concentrations initially present, for how they change as the reaction proceeds, and for what they are when the system reaches equilibrium. The acronym ICE is commonly used to refer to this mathematical approach, and the concentrations terms are usually gathered in a tabular format called an ICE table.

Example 1

Calculation of an Equilibrium Constant

Iodine molecules react reversibly with iodide ions to produce triiodide ions.

[latex]\text{I}_2(aq)\;+\;\text{I}^{-}(aq)\;{\rightleftharpoons}\;\text{I}_3^{\;\;-}(aq)[/latex]

If a solution with the concentrations of I2 and I− both equal to 1.000 × 10−3 M before reaction gives an equilibrium concentration of I2 of 6.61 × 10−4 M, what is the equilibrium constant for the reaction?

SOLUTION
We will begin this problem by calculating the changes in concentration as the system goes to equilibrium. Then we determine the equilibrium concentrations and, finally, the equilibrium constant. First, we set up a table with the initial concentrations, the changes in concentrations, and the equilibrium concentrations using −x as the change in concentration of I2.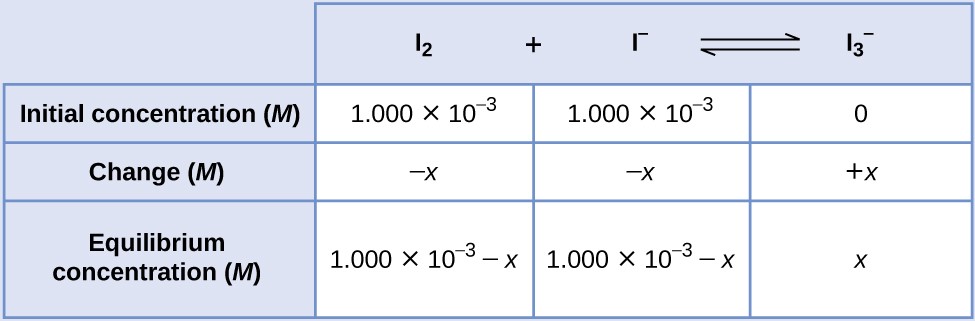

Since the equilibrium concentration of I2 is given, we can solve for x. At equilibrium the concentration of I2 is 6.61 × 10−4 M so that

[latex]\begin{eqnarray} \left(1.000\;\times\;10^{-3}\right)\;-\;x &=& 6.61\;\times\;10^{-4} \\ \left(1.000\;\times\;10^{-3}\right)\;-\;\left(6.61\;\times\;10^{-4}\right) &=& x\\ 3.39\;\times\;10^{-4}\;\text{M} &=& x \end{eqnarray}[/latex]

Now we can fill in the table with the concentrations at equilibrium.
This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), Equilibrium concentration ( M ). The second column has the header, “I subscript 2 plus sign I superscript negative sign equilibrium arrow I subscript 3 superscript negative sign.” Under the second column is a subgroup of three rows and three columns. The first column has the following: 1.000 times 10 to the negative third power, negative x equals negative 3.39 times 10 to the negative fourth power, 6.61 times 10 to the negative fourth power. The second column has the following: 1.000 times 10 to the negative third power, negative x, 6.61 times 10 to the negative fourth power. The third column has the following: 0, positive x, 3.39 times 10 to the negative fourth power.

We now calculate the value of the equilibrium constant.

[latex]K_\text{c} = Q_\text{c} = \frac{[\text{I}_3^{\;\;-}]}{[\text{I}_2][\text{I}^{-}]} = \frac{3.39\;\times\;10^{-4}}{(6.61\;\times\;10^{-4})(6.61\;\times\;10^{-4})} = \boxed{776}[/latex]

Calculation of a Missing Equilibrium Concentration

When the equilibrium constant and all but one equilibrium concentration are provided, the other equilibrium concentration(s) may be calculated. A computation of this sort is illustrated in the next example exercise.

Example 2

Calculation of a Missing Equilibrium Concentration

Nitrogen oxides are air pollutants produced by the reaction of nitrogen and oxygen at high temperatures. At 2000 °C, the value of the equilibrium constant for the reaction, [latex]\text{N}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{NO}(g)[/latex], is 4.1 × 10−4. Find the concentration of NO(g) in an equilibrium mixture with air at 1 atm pressure at this temperature. In air, [N2] = 0.036 mol/L and [O2] 0.0089 mol/L.

SOLUTION
We are given all of the equilibrium concentrations except that of NO. Thus, we can solve for the missing equilibrium concentration by rearranging the equation for the equilibrium constant.

[latex]\begin{eqnarray} K_\text{c} &=& \frac{[\text{NO}]^2}{[\text{N}_2][\text{O}_2]} \\[0.2em] K_\text{c}[\text{N}_2][\text{O}_2] &=& [\text{NO}]^2 \\[0.2em] \sqrt{K_\text{c}[\text{N}_2][\text{O}_2]} &=& [\text{NO}]\\[0.2em] \sqrt{(4.1\;\times\;10^{-4})(0.036)(0.0089)} &=& [\text{NO}]\\[0.2em] \sqrt{1.31\;\times\;10^{-7}} &=& [\text{NO}]\\[0.2em] \boxed{3.6\;\times\;10^{-4} \text{ M}}&=& [\text{NO}] \end{eqnarray}[/latex]

Thus [NO] is 3.6 × 10−4 mol/L at equilibrium under these conditions.

We can check our answer by substituting all equilibrium concentrations into the expression for the reaction quotient to see whether it is equal to the equilibrium constant.

[latex]Q_\text{c} = \frac{[\text{NO}]^2}{[\text{N}_2][\text{O}_2]} = \frac{(3.6\;\times\;10^{-4})^2}{(0.036)(0.0089)} = 4.0\;\times\;10^{-4} = K_\text{c}[/latex]

The answer checks; our calculated value gives the equilibrium constant within the error associated with the significant figures in the problem.

Calculation of Equilibrium Concentrations from Initial Concentrations

Perhaps the most challenging type of equilibrium calculation can be one in which equilibrium concentrations are derived from initial concentrations and an equilibrium constant. For these calculations, a four-step approach is typically useful:

  1. Identify the direction in which the reaction will proceed to reach equilibrium.
  2. Develop an ICE table.
  3. Calculate the concentration changes and, subsequently, the equilibrium concentrations.
  4. Confirm the calculated equilibrium concentrations.

Example 3

Calculation of Concentration Changes

Under certain conditions, the equilibrium constant for the decomposition of PCl5(g) into PCl3(g) and Cl2(g) is 0.0211. What are the equilibrium concentrations of PCl5, PCl3, and Cl2 if the initial concentration of PCl5 was 1.00 M?

SOLUTION
Use the stepwise process described earlier.

  1. Determine the direction the reaction proceeds.

    The balanced equation for the decomposition of PCl5 is

    [latex]\text{PCl}_5(g)\;{\rightleftharpoons}\;\text{PCl}_3(g)\;+\;\text{Cl}_2(g)[/latex]

    Because we have no products initially, Qc = 0 and the reaction will proceed to the right.

  2. Determine the relative changes needed to reach equilibrium, then write the equilibrium concentrations in terms of these changes.

    Let us represent the increase in concentration of PCl3 by the symbol x. The other changes may be written in terms of x by considering the coefficients in the chemical equation.

    [latex]\begin{array}{lcccc} \text{PCl}_5(g) & {\rightleftharpoons} & \text{PCl}_3(g) & + & \text{Cl}_2(g) \\[0.5em] -x & & +x & & +x \end{array}[/latex]

    The changes in concentration and the expressions for the equilibrium concentrations are:
    This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), Equilibrium concentration ( M ). The second column has the header, “P C l subscript 5 equilibrium arrow P C l subscript 3 plus C l subscript 2.” Under the second column is a subgroup of three rows and three columns. The first column has the following: 1.00, negative x, 1.00 minus x. The second column has the following: 0, positive x, 0 plus x equals x. The third column has the following: 0, positive x, 0 plus x equals x.

  3. Solve for the change and the equilibrium concentrations.

    Substituting the equilibrium concentrations into the equilibrium constant equation gives

    [latex]K_\text{c} = \frac{[\text{PCl}_3][\text{Cl}_2]}{[\text{PCl}_5]} = 0.0211 = \frac{(x)(x)}{(1.00\;-\;x)}[/latex]

    This equation contains only one variable, x, the change in concentration. We can write the equation as a quadratic equation and solve for x using the quadratic formula.

    [latex]\begin{eqnarray} 0.0211 &=& \frac{(x)(x)}{(1.00\;-\;x)} \\[0.5em] 0.0211(1.00\;-\;x) &=& x^2 \\ x^2\;+\;0.0211x\;-\;0.0211 &=& 0 \end{eqnarray}[/latex]

    An equation of the form ax2 + bx + c = 0 can be rearranged to solve for x:

    [latex]x = \frac{-b\;{\pm}\;\sqrt{b^2\;-\;4ac}}{2a}[/latex]

    In this case, a = 1, b = 0.0211, and c = −0.0211. Substituting the appropriate values for a, b, and c yields:

    [latex]x = \frac{-0.0211\;{\pm}\;\sqrt{(0.0211)^2\;-\;4(1)(-0.0211)}}{2(1)}[/latex]
    [latex]= \frac{-0.0211\;{\pm}\;\sqrt{(4.45\;\times\;10^{-4})\;+\;(8.44\;\times\;10^{-2})}}{2}[/latex]
    [latex]= \frac{-0.0211\;{\pm}\;0.291}{2}[/latex]

    Hence

    [latex]x = \frac{-0.0211\;+\;0.291}{2} = 0.135[/latex]

    or

    [latex]x = \frac{-0.0211\;-\;0.291}{2} = -0.156[/latex]

    Quadratic equations often have two different solutions, one that is physically possible and one that is physically impossible (an extraneous root). In this case, the second solution (−0.156) is physically impossible because we know the change must be a positive number (otherwise we would end up with negative values for concentrations of the products). Thus, x = 0.135 M.

    The equilibrium concentrations are

    [latex][\text{PCl}_5] = 1.00\;-\;0.135 = 0.86\;\text{M}[/latex]
    [latex][\text{PCl}_3] = x = 0.135\;\text{M}[/latex]
    [latex][\text{Cl}_2] = x = 0.135\;\text{M}[/latex]
  4. Check the arithmetic.

    Substitution into the expression for Kc (to check the calculation) gives

    [latex]K_\text{c} = \frac{[\text{PCl}_3][\text{Cl}_2]}{[\text{PCl}_5]} = \frac{(0.135)(0.135)}{0.87} = 0.021[/latex]

    The equilibrium constant calculated from the equilibrium concentrations is equal to the value of Kc given in the problem (when rounded to the proper number of significant figures). Thus, the calculated equilibrium concentrations check.

    The % change in reactant concentration is

    [latex]\dfrac{x}{\text{initial } [\text{PCl}_5]}=\frac{0.135 \text{ M}}{1.00 \text{ M}}=0.135 = 13.5\%[/latex]

    The % change is >5% and thus we could not have simplified the solution by approximating 1.00 − x to 1.00.

Example 4

Bromine monochloride is an interhalogen compound that can be synthesized as

Br2(g) + Cl2(g) ⇌ 2 BrCl(g), Kp = 4.7 × 10–2

A vessel initially contains 0.115 atm of Br2(g) and 0.776 atm of BrCl(g).  What is the partial pressure of each species of the reaction at equilibrium?

SOLUTION

The reaction quotient is

[latex]Q_{\text{p}}=\frac{P_{\text{BrCl}}^2}{P_{\text{Br}_2}P_{\text{Cl}_2}}=\frac{0.776}{0(0.115)}\rightarrow\infty > K_\text{p}[/latex]

The reaction will shift left.

Construct an ICE table using the initial partial pressures and indicate the direction of the change.

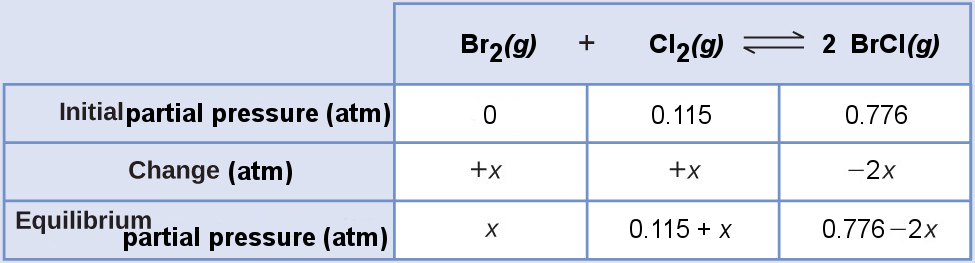
Substitute the equilibrium partial pressures into the Kp expression,

[latex]\begin{array}{r l} K_\text{p} &= \frac{P_{\text{BrCl}}^2}{P_{\text{Br}_2}P_{\text{Cl}_2}} \\ 4.7×10^{–2} &= \frac{(0.776-2x)^2}{x(0.115+x)} \end{array}[/latex]

Expand the equation and collect like terms,

[latex]0.602-3.10x+4x^2 = 5.41×10^{-3}x+4.7×10^{-2}x^2 \\ 3.95x^2 -3.11x+0.602 = 0[/latex]

Substitute the coefficients and constant term of the quadratic equation into the quadratic formula and solve for x,

[latex]x=\frac{-(-3.11)\pm\sqrt{(-3.11)^2-4(3.95)(0.602)}}{2(3.95)}=0.442, 0.345[/latex]

Notice that [latex]x=0.442[/latex] is an extraneous root because the expression [latex]0.776-2x=0.776-2(0.442)=-0.108[/latex] evaluates to a negative partial pressure.  The equilibrium partial pressures are

[latex]\begin{array}{rl} P_{\text{Br}_2} &= \boxed{0.345 \text{ atm}} \\ P_{\text{Cl}_2} &= 0.115 \text{ atm}+0.345\text{ atm} = \boxed{0.460 \text{ atm}} \\ P_{\text{BrCl}} &= 0.776\text{ atm}-2(0.345\text{ atm}) = \boxed{0.086 \text{ atm}} \end{array}[/latex]

Check that the equilibrium partial pressures match the Kp value,

[latex]K_{\text{p}}=\frac{(0.086)^2}{(0.345)(0.460)}= 4.7×10^{–2}[/latex]

Optional Resources

Watch videos about the equilibrium constant, equilibrium quotient, and how to perform ICE table calculations.

Video 1 Equilibrium (12 min 23 s).

Video 2 Equilibrium Made Easy: How to Solve Chemical Equilibrium Problems (12 min 42 s). This video uses the acronym RICE.  The R stands for “reaction” and is not a different table than the ICE table.

✐ SELF-CHECK QUESTION
Consider the following reaction and its equilibrium constant:

4 CuO(s) + CH4(g) ⇌ CO2(g) + 4 Cu(s) + 2 H2O(s)      Kc = 1.10

A reaction mixture contains 0.22 mol/L CH4, 0.67 mol/L CO2, and significant amounts of all solids. Which of the following statements is true concerning this system?

A) The reaction will proceed to make more products.
B) The equilibrium constant will increase.
C) The reaction quotient will increase.
D) The reaction will proceed to make more reactants.
E) The system is at equilibrium.

Click to see answer

D) The reaction will proceed to make more reactants.

[latex]\begin{align*} Q_{\text{c}}&=\frac{[\text{CO}_2]}{[\text{CH}_4]} \\ &=\frac{0.67}{0.22} \\ &=3.0 > 1.10 = K_{\text{c}} \end{align*}[/latex] 


✩ UNIT 3 ASSIGNMENT

Complete Unit 3 Assignment (graded) on Moodle.  This assignment is worth 11% of the course grade.

License

Icon for the Creative Commons Attribution 4.0 International License

3.4 Equilibrium Calculations Copyright © by OpenStax is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book