Unit 4 Acid-Base and Solubility Equilibria
4.4 Acid-Base Reactions and Buffer Solutions
OpenStax
Section Learning Objectives
- Describe the composition and function of acid–base buffers.
- Calculate the pH of a buffer before and after the addition of added acid or base.
✓ SECTION 4.4 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion. | No | 20 min |
| Optional Resource: Watch the video on the buffer system encountered in natural waters. | No | 12 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 20 min |
📖 READING PORTION
A solution containing appreciable amounts of a weak conjugate acid-base pair is called a buffer solution, or a buffer. Buffer solutions resist a change in pH when small amounts of a strong acid or a strong base are added (Figure 1). A solution of acetic acid and sodium acetate (CH3COOH + CH3COONa) is an example of a buffer that consists of a weak acid and its salt. An example of a buffer that consists of a weak base and its salt is a solution of ammonia and ammonium chloride (NH3 + NH4Cl).

How Buffers Work
To illustrate the function of a buffer solution, consider a mixture of roughly equal amounts of acetic acid and sodium acetate. The presence of a weak conjugate acid-base pair in the solution imparts the ability to neutralize modest amounts of added strong acid or base. For example, strong base added to this solution will neutralize hydronium ion, causing the acetic acid ionization equilibrium to shift to the right and generate additional amounts of the weak conjugate base (acetate ion)
CH3COOH(aq) + H2O(l) ⇌ H3O+(aq) + CH3COO−(aq)
Likewise, strong acid added to this buffer solution will shift the above ionization equilibrium left, producing additional amounts of the weak conjugate acid (acetic acid). The buffering action of the solution is essentially a result of the added strong acid and base being converted to the weak acid and base that make up the buffer’s conjugate pair. The weaker acid and base undergo only slight ionization, as compared with the complete ionization of the strong acid and base, and the solution pH, therefore, changes much less drastically than it would in an unbuffered solution.
Example 1
pH Changes in Buffered and Unbuffered Solutions
Acetate buffers are used in biochemical studies of enzymes and other chemical components of cells to prevent pH changes that might affect the biochemical activity of these compounds.
(a) Calculate the pH of an acetate buffer that is a mixture with 0.10 M acetic acid (CH3CO2H) and 0.10 M sodium acetate (CH3CO2Na).
(b) Calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of this buffer.
(c) For comparison, calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of a solution of an unbuffered solution of a monoprotic strong acid with a pH of 4.74.
SOLUTION
(a) Following the ICE approach to this equilibrium calculation yields the following:
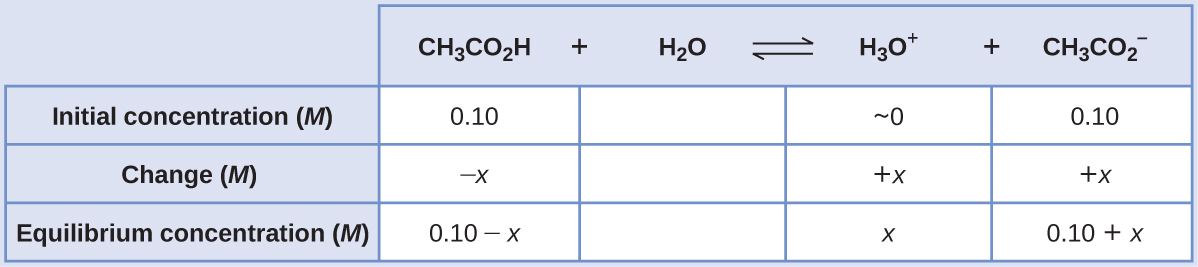
Substituting the equilibrium concentration terms into the Ka expression, assuming x << 0.10, and solving the simplified equation for x yields
x = 1.8 × 10−5 M
[latex][\text{H}_3\text{O}^+] = 0+x =1.8×10^{−5} \text{ M}[/latex]
[latex]\text{pH}=−\log[\text{H}_3\text{O}^+]=−\log(1.8×10^{−5})=\boxed{4.74}[/latex]
(b) Calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of this buffer.
Adding strong base will neutralize some of the acetic acid, yielding the conjugate base acetate ion. Compute the new concentrations of these two buffer components, then repeat the equilibrium calculation of part (a) using these new concentrations.
0.0010 L × (0.10 mol NaOH / 1 L) = 1.0 × 10−4 mol NaOH
The initial molar amount of acetic acid is
0.100 L × (0.100 mol CH3CO2H / 1 L) = 1.00 × 10−2 mol CH3CO2H
The amount of acetic acid remaining after some is neutralized by the added base is
(1.0 × 10−2) − (0.01 × 10−2) = 0.99 × 10−2 mol CH3CO2H
The newly formed acetate ion, along with the initially present acetate, gives a final acetate concentration of
(1.0 × 10−2) + (0.01 × 10−2) = 1.01 × 10−2 mol CH3CO2Na
Compute molar concentrations for the two buffer components:
[CH3CO2H] = 9.9 × 10−3 mol / 0.101 L = 0.098 M
[CH3CO2Na] = 1.01 × 10−2 mol / 0.101 L = 0.100 M
Using these concentrations, the pH of the solution may be computed as in part (a) above, yielding pH = 4.75 (only slightly different from that prior to adding the strong base).
A shortcut to solving this question is to assume that the total solution volume does not increase appreciably from adding a small amount of NaOH. The increase in volume affects the conjugate acid-base pair equally. After adding NaOH, [CH3CO2H] = 0.100 M − 0.0010 M = 0.099 M and [CH3CO2−] = 0.100 M + 0.0010 M = 1.010 M.
(c) For comparison, calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of a solution of an unbuffered solution of a monoprotic strong acid with a pH of 4.74.
The amount of hydronium ion initially present in the solution is
[latex][\text{H}_3\text{O}^+]=10^{-\text{pH}}=10^{−4.74}=1.8×10^{−5} \text{ M}[/latex]
mol H3O+ = (0.100 L)(1.8 × 10−5 M) = 1.8 × 10−6 mol H3O+
The amount of hydroxide ion added to the solution is
mol OH− = (0.0010 L)(0.10 M) = 1.0 × 10−4 mol OH−
The added hydroxide will neutralize hydronium ion via the reaction
H3O+(aq) + OH−(aq) ⇌ 2 H2O(l)
The 1:1 stoichiometry of this reaction shows that an excess of hydroxide has been added (greater molar amount than the initially present hydronium ion).
The amount of hydroxide ion remaining is
(1.0 × 10−4 mol) − (1.8 × 10−6 mol) = 9.8 × 10−5 mol OH−
corresponding to a hydroxide molarity of
9.8 × 10−5 mol OH− / 0.101 L = 9.7 × 10−4 M
The pH of the solution is then calculated to be
[latex]\text{pH}=14.00−\text{pOH}=14.00−\log(9.7×10^{−4})=\boxed{10.99}[/latex]
In this unbuffered solution, addition of the base results in a significant rise in pH (from 4.74 to 10.99) compared with the very slight increase observed for the buffer solution in part (b) (from 4.74 to 4.75).
The Henderson-Hasselbalch Equation
Scientists often use an equation, called the Henderson-Hasselbalch equation, to calculate the pH of buffer solutions.
Equation 1
[latex]\text{pH}=\text{p}K_{\text{a}}+\log\frac{[\text{A}^−]}{[\text{HA}]}[/latex]
It is important to note that the “x is small” assumption must be valid to use this equation. The pKa is the negative of the logarithm of the ionization constant of the weak acid (pKa = −log Ka). This equation relates the pH, the ionization constant of a weak acid, and the concentrations of the weak conjugate acid-base pair in a buffered solution.
The ionization-constant expression for a solution of a weak acid can be written as
[latex]K_{\text{a}}=\frac{[\text{H}_3\text{O}^+][\text{A}^−]}{[\text{HA}]}[/latex]
Rearranging to solve for [H3O+] yields
[latex][\text{H}_3\text{O}^+]=\frac{K_{\text{a}}×[\text{HA}]}{[\text{A}^−]}[/latex]
Taking the negative logarithm of both sides of this equation gives
[latex]−\log[\text{H}_3\text{O}^+]=−\log K_{\text{a}}− \log \frac{[\text{HA}]}{[\text{A}^−]}[/latex],
which can be written as
[latex]\text{pH}=\text{p}K_{\text{a}}+\log\frac{[\text{A}^−]}{[\text{HA}]}[/latex]
Example 2
Use Equation 1 to calculate the pH in Example 1 parts (a) and (b). The Ka of acetic acid is 1.8 × 10−5.
SOLUTION
(a) We have the concentration of the buffer components as [CH3CO2H] = 0.10 M and [CH3CO2Na] = [CH3CO2−] = 0.10 M.
[latex]\text{pH}=\text{p}K_{\text{a}}+\log\frac{[\text{A}^−]}{[\text{HA}]}[/latex]
[latex]\text{pH}=-\log(1.8×10^{-5})+\log\frac{0.10}{0.10} = \boxed{4.74}[/latex]
(b) The concentration of acetic acid and acetate ion after adding NaOH is [CH3CO2H] = 0.098 M and [CH3CO2Na] = [CH3CO2−] = 0.100 M.
[latex]\text{pH}=\text{p}K_{\text{a}}+\log\frac{[\text{A}^−]}{[\text{HA}]}[/latex]
[latex]\text{pH}=-\log(1.8×10^{-5})+\log\frac{0.100}{0.098} = \boxed{4.75}[/latex]
Example 3
Comparing an Unbuffered and Buffered Basic Solution
Calculate the pH after adding 1.00 mL of 0.100 M HCl to the following solutions:
(a) 100 mL solution of a monoprotic strong base, pH 9.80.
(b) 100 mL solution of 0.200 M trimethylamine (Kb = 6.3 × 10−5) with 0.200 M of the conjugate acid salt, trimethylammonium chloride.
SOLUTION
The H3O+ concentration after adding 1.00 mL of 0.100 M HCl to 100 mL of solution is approximately
[latex][\text{H}_3\text{O}^+]=(1.00\times10^{-3} \text{ L})(0.100 \text{ M})\;/\;0.100\text{ L} = 0.00100 \text{ M}[/latex]
This is the H3O+ concentration that reacts with (a) OH− and (b) trimethylamine.
(a) Initially, the pH 9.80 solution has
[latex]\text{pOH} = 14.00 - \text{pH} = 14.00 - 9.80 = 4.20[/latex]
[latex][\text{OH}^-]=10^{-\text{pOH}} = 10^{-4.20}=6.3 \times10^{-5} \text{ M}[/latex]
The leftover [H3O+] and pH after reacting with 6.3 × 10−5 M of OH− is
[latex][\text{H}_3\text{O}^+]=0.00100 \text{ M} - 0.000063 \text{ M} = 0.00094 \text{ M}[/latex]
[latex]\text{pH} = -\log(0.00094)= \boxed{3.03}[/latex]
(b) The solution is a mixture of weak acid-weak base conjugate pairs, and the pH is
[latex]\text{pH} = -\log(K_{\text{a}})+\log\frac{[\text{A}^−]}{[\text{HA}]}[/latex]
[latex]\text{pH} = -\log\frac{K_{\text{w}}}{K_{\text{b}}}+\log\frac{[\text{A}^−]}{[\text{HA}]}[/latex]
[latex]\text{pH} = -\log\left(\frac{1.0\times10^{-14}}{6.3\times10^{-5}}\right)+\log\left(\frac{0.200 \text{ M}}{0.200 \text{ M}}\right) = 9.80[/latex]
The HCl reacts with trimethylamine to form the trimethylammonium ion
[latex][\text{trimethylamine}] = 0.200 \text{ M} - 0.00100 \text{ M} = 0.199 \text{ M}[/latex]
[latex][\text{trimethylammonium ion}] = 0.200 \text{ M} + 0.00100 \text{ M} = 0.201 \text{ M}[/latex]
[latex]\text{pH} = -\log\left(\frac{1.0\times10^{-14}}{6.3\times10^{-5}}\right)+\log\left(\frac{0.199 \text{ M}}{0.201 \text{ M}}\right) = \boxed{9.80}[/latex]
Noticed that adding HCl to the unbuffered, dilute solution of strong base decreased the pH from 9.80 to 3.03. Adding the same amount of HCl to the buffered solution did not noticeably change the pH.
The weak acid component of a buffer solution has better neutralizing capacity than very dilute strong acid solutions at the same pH (Example 1). Similarly, in Example 3, we see that the weak base component of a buffer solution is better at resisting the decrease in pH compared to the dilute strong base. Buffers are only effective when both the conjugate acid and conjugate base concentrations are large enough and the ratio of both concentrations is within 0.1 to 10 range. This means that the effective pH range for buffers is pKa ± 1 according to the Henderson-Hasselbalch equation.
The next examples explore how a solution of an unbuffered weak acid (Example 4) or an unbuffered weak base (Example 5) has a moderate ability to resist pH change. The unbuffered weak acid/base solution is better than an unbuffered strong acid/base, but worse than a buffer solution, at resisting pH change.
Example 4
Comparing an Unbuffered and Buffered Acidic Solution
An unbuffered solution contains 0.200 M of a hypothetical monoprotic weak acid (HA) at pH 4.74. Calculate the pH after 1.00 mL of 0.100 M NaOH is added to 100 mL of the weak acid.
SOLUTION
The Ka of the weak acid HA is
[latex]\text{HA} + \text{H}_2\text{O} \rightleftharpoons \text{A}^-+\text{H}_3\text{O}^+[/latex]
[latex][\text{H}_3\text{O}^+] = 10^{-\text{pH}}=10^{-4.74} = 1.8\times10^{-5} \text{ M}[/latex], call this concentration as x, then
[latex]\begin{align*} K_{\text{a}} &= \frac{[\text{H}_3\text{O}^+][\text{A}^-]}{[\text{HA}]} \\ &=\frac{x\cdot x}{[\text{HA}]_{\text{initial}}-x} \\&=\frac{\left(1.8\times10^{-5}\right) \left(1.8\times10^{-5}\right)}{0.200-\left(1.8\times10^{-5}\right)} \\ &=1.7\times10^{-9} \end{align*}[/latex]
The OH– concentration after adding 1.00 mL of 0.100 M NaOH to 100 mL of solution is approximately
[latex][\text{OH}^-]=(1.00\times10^{-3} \text{ L})(0.100 \text{ M})\;/\;0.100\text{ L} = 0.00100 \text{ M}[/latex]
The OH– reacts with HA to form the conjugate base, A–
[latex][\text{HA}] = 0.200 \text{ M}-0.00100 \text{ M} = 0.199 \text{ M}[/latex]
[latex][\text{A}^-] = 0.00100 \text{ M}[/latex]
The pH for the mixture of weak conjugate acid-weak conjugate base is
[latex]\begin{align*} \text{pH} &= -\text{p}K_{\text{a}}+\log\frac{[\text{A}^-]}{[\text{HA}]} \\ &= -\log\left(K_{\text{a}}\right)+\log\frac{[\text{A}^-]}{[\text{HA}]} \\ &=-\log(1.7\times10^{-9})+\log\left(\frac{0.00100 \text{ M}}{0.199\text{ M}}\right) \\ &=\boxed{6.48} \end{align*}[/latex]
Example 5
Comparing an Unbuffered and Buffered Basic Solution
An unbuffered solution contains 0.400 M of a hypothetical monoprotic weak base (B) at pH 9.80. Calculate the pH after 1.00 mL of 0.100 M HCl is added to 100 mL of the weak base.
SOLUTION
The Kb of the weak base B is
[latex]\text{B} + \text{H}_2\text{O} \rightleftharpoons \text{HB}^+ + \text{OH}^-[/latex]
[latex]\text{pOH} = 14.00 - \text{pH} = 14.00 - 9.80 = 4.20[/latex]
[latex][\text{OH}^-] = 10^{-\text{pOH}}=10^{-4.20} = 6.3\times10^{-5} \text{ M}[/latex], call this concentration as x, then
[latex]\begin{align*} K_{\text{b}} &= \frac{[\text{OH}^-][\text{HB}^+]}{[\text{B}]} \\ &=\frac{x\cdot x}{[\text{B}]_{\text{initial}}-x} \\ &=\frac{\left(6.3\times10^{-5}\right) \left(6.3\times10^{-5}\right)}{0.400-\left(6.3\times10^{-5}\right)} \\ &=9.95\times10^{-9} \end{align*}[/latex]
The H3O+ concentration after adding 1.00 mL of 0.100 M HCl to 100 mL of solution is approximately
[latex][\text{H}_3\text{O}^+]=(1.00\times10^{-3} \text{ L})(0.100 \text{ M})\;/\;0.100\text{ L} = 0.00100 \text{ M}[/latex]
The H3O+ reacts with B to form the conjugate acid, HB+
[latex][\text{B}] = 0.400 \text{ M}-0.00100 \text{ M} = 0.399 \text{ M}[/latex]
[latex][\text{HB}^+] = 0.00100 \text{ M}[/latex]
The pH for the mixture of weak conjugate base-weak conjugate acid is
[latex]\begin{align*} \text{pH} &= -\text{p}K_{\text{a}}+\log\frac{[\text{A}^-]}{[\text{HA}]} \\ &= -\log\left(K_{\text{a}}\right)+\log\frac{[\text{B}]}{[\text{HB}^+]} \\ &= -\log\left(\frac{K_{\text{w}}}{K_{\text{b}}}\right)+\log\frac{[\text{B}]}{[\text{HB}^+]} \\ &=-\log\left(\frac{1.0\times10^{-14}}{9.95\times10^{-9}}\right)+\log\left(\frac{0.399 \text{ M}}{0.00100 \text{ M}}\right) \\ &=\boxed{8.60} \end{align*}[/latex]
We see that adding the same amount of a strong base, 1.0 mL of 0.10 M NaOH, to acidic solutions initially at pH 4.74 dramatically increases the pH of the unbuffered strong acid (Example 1(c), pH 10.99) and moderately increases the pH of the unbuffered weak acid (Example 4, pH 6.48). However, the acidic buffer solution has the smallest pH increase, from pH 4.74 to 4.75 (Example 1(b)). The unbuffered strong acid is worse at resisting pH increase than an unbuffered weak acid when the same amount of strong base is added to the solution. The buffer solution is the best at resisting pH increase.
Moreover, adding the same amount of a strong acid decreases the pH the most for the unbuffered strong base (Example 3(a), pH 3.30) and less so for the unbuffered weak base (Example 5, pH 8.60), even though both solutions are initially at pH 9.80. The basic buffer solution has a negligible change in pH (Example 3(b)). Hence, buffers are more capable at resisting pH change than unbuffered weak acids/bases, and unbuffered dilute strong acids/bases at the same pH have limited ability in maintaining a constant pH.
Optional Resource
Watch this video on the buffer system encountered in natural waters.
Video 1 Buffers, the Acid Rain Slayer: Crash Course Chemistry #31 (11 min 40 s).
Video 2 Weak base–strong acid titrations | Acids and bases | AP Chemistry | Khan Academy (10 min 33 s).
Which statement about buffers is true?
A) Buffers minimally change in pH upon addition of small amounts of strong acid or strong base.
B) Buffers do not change pH on addition of a strong acid or strong base.
C) Buffers consist of a strong acid and its conjugate base.
D) Buffers have a pH = 7.
Click to see answer
A) Buffers minimally change in pH upon addition of small amounts of strong acid or strong base.

