Unit 5 Thermodynamics
5.1 The First Law of Thermodynamics
OpenStax
Section Learning Objectives
- Define heat, work, and internal energy.
- Compute the change in internal energy of a system.
✓ SECTION 5.1 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion. | No | 30 min |
| Optional Resource: Read about how car engines work. | No | 60 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 20 min |
📖 READING PORTION
Thermochemistry is a branch of chemical thermodynamics, the science that deals with the relationships between heat, work, and other forms of energy in the context of chemical and physical processes. As we concentrate on thermochemistry, we need to consider some widely used concepts of thermodynamics.
Heat
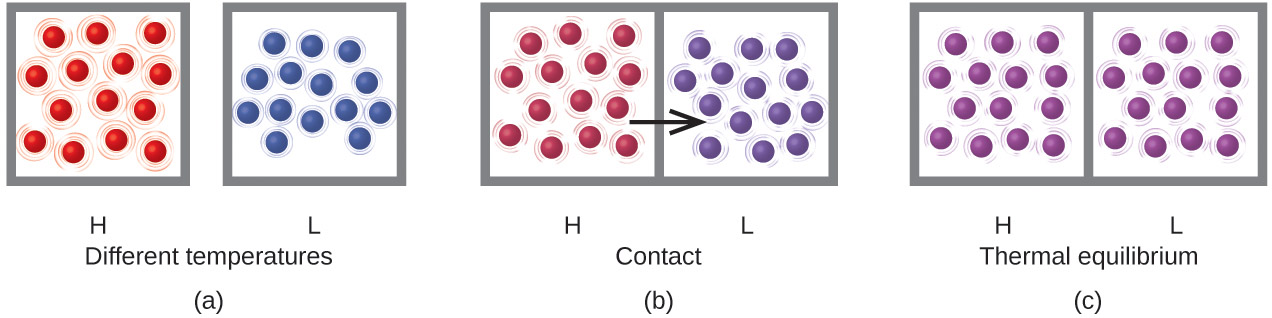
Heat (q) is the transfer of thermal energy between two bodies at different temperatures. Heat flow (a redundant term, but one commonly used) increases the thermal energy of one body and decreases the thermal energy of the other until both bodies are at the same temperature, thermal equilibrium. Suppose we initially have a high temperature (and high thermal energy) substance (H) and a low temperature (and low thermal energy) substance (L), Figure 1(a). The atoms and molecules in H have a higher average kinetic energy than those in L. If we place substance H in contact with substance L, the thermal energy will flow spontaneously from substance H to substance L, Figure 1(b). The temperature of substance H will decrease, as will the average kinetic energy of its molecules; the temperature of substance L will increase, along with the average kinetic energy of its molecules. Heat flow will continue until the two substances are at the same temperature, Figure 1(c).
Matter undergoing chemical reactions and physical changes can release or absorb heat. A change that releases heat is called an exothermic process. For example, the combustion reaction that occurs when using an oxyacetylene torch is an exothermic process—this process also releases energy in the form of light as evidenced by the torch’s flame, Figure 2(a). A reaction or change that absorbs heat is an endothermic process. A cold pack used to treat muscle strains provides an example of an endothermic process. When the substances in the cold pack (water and a salt like ammonium nitrate) are brought together, the resulting process absorbs heat, leading to the sensation of cold, Figure 2(b).

Work
There are multiple forms of work. For example, we perform work when we exert force to push an object, and the object moves a certain distance in the direction that we push. Here, we are interested in a type of work called expansion work (or pressure-volume work), which occurs when an object expands against a restraining pressure, or when an external pressure compresses the object. The object, called the system, can be an enclosed volume or even a chemical reaction and is distinct from the surroundings.
For pressure-volume work at constant pressure (P), the definition of work (w) is
Equation 1
[latex]w = -P\Delta V[/latex]
- [latex]w[/latex], work ([latex]\text{J}[/latex])
- [latex]P[/latex], pressure ([latex]\text{Pa}[/latex])
- [latex]\Delta V[/latex], change in volume ([latex]\text{m}^3[/latex])
The units for pressure and volume are not restricted to Pa and m3, respectively, as long as the units for these two variables multiply to yield a unit of energy.
When an object expands, the change in volume (ΔV) is a positive quantity, and work is negative. One may say that work leaves the system as the system pushes against the surroundings. When a system contracts, the change in volume is a negative quantity, and work is positive. The system gains energy as the surroundings do work on the system.
Internal Energy
Substances act as reservoirs of energy, meaning that energy can be added to them or removed from them. Energy is stored in a substance when the kinetic energy of its atoms or molecules is raised, such as by increasing the temperature of the substance. Recall from Section 1.3 that temperature is a measure of the average kinetic energy of the particles of a substance. The greater kinetic energy may result in increased translations (travel or straight-line motions), vibrations, or rotations of the atoms or molecules. When thermal energy (heat) is lost, the intensities of these motions decrease and the kinetic energy falls. The total of all possible kinds of energy present in a substance is called the internal energy (U), sometimes symbolized as E.
As a system undergoes a change, its internal energy can change, and energy can be transferred from the system to the surroundings, or from the surroundings to the system. Energy is transferred into a system, an increase in internal energy, when it absorbs heat from the surroundings or when the surroundings do work on the system. For example, energy is transferred into room-temperature metal wire if it is immersed in hot water (the wire absorbs heat from the water), or if we rapidly bend the wire back and forth (the wire becomes warmer because of the work done on it). Both processes increase the internal energy of the wire, which is reflected in an increase in the wire’s temperature.
Conversely, internal energy is transferred out of a system when heat is lost from the system, or when the system does work on the surroundings. An example of this occurs during the operation of an internal combustion engine. The reaction of gasoline and oxygen is exothermic. Some of this energy is given off as heat, and some does work pushing the piston in the cylinder. The substances involved in the reaction are the system, and the engine and the rest of the universe are the surroundings. The system loses energy by both heating and doing work on the surroundings, and its internal energy decreases. (The engine is able to keep the car moving because this process is repeated many times per second while the engine is running.)
The internal energy change (ΔU) of a system is the net change in energy from the transfer of heat or work to or from the system. The relationship between internal energy, heat, and work can be represented by the equation
Equation 2
[latex]\Delta U = q + w[/latex]
- [latex]\Delta U[/latex], change in internal energy of a system ([latex]\text{J}[/latex])
- [latex]q[/latex], heat transferred to or from a system ([latex]\text{J}[/latex])
- [latex]w[/latex], work performed by or on a system ([latex]\text{J}[/latex])
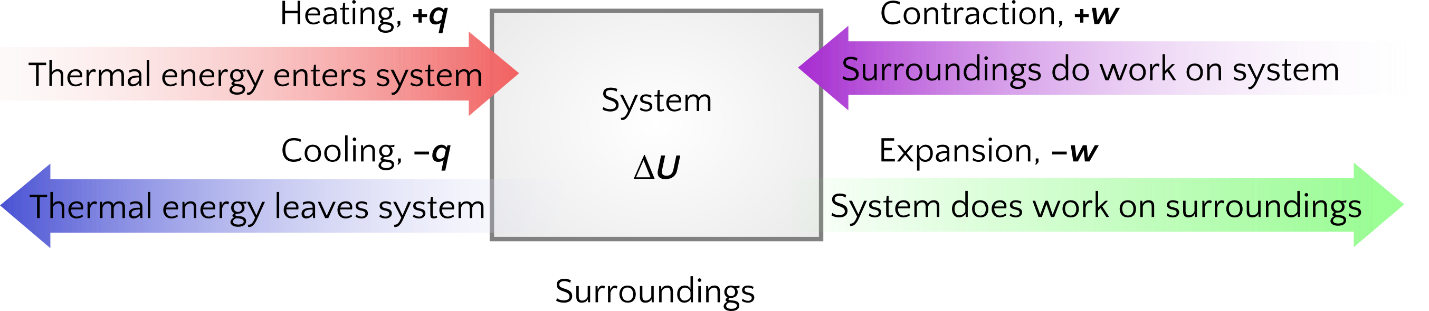
In general chemistry, we only deal with the change in internal energy (ΔU) rather than the absolute quantity of internal energy (U). In engineering thermodynamics courses, we may refer to both ΔU and U. The First Law of Thermodynamics states that energy cannot be created or destroyed but can be converted from one form to another. Hence, internal energy, heat, and work are different forms in which energy can be converted. Note that our sign convention is:
- positive ΔU, the system gains internal energy
- negative ΔU, the system loses internal energy
- positive q, heat flowing into the system
- negative q, heat flowing out of the system
- positive w, work done on the system
- negative w, work done by the system
The sign convention is summarized in Figure 3. Other courses and employment settings may use different sets of sign conventions.
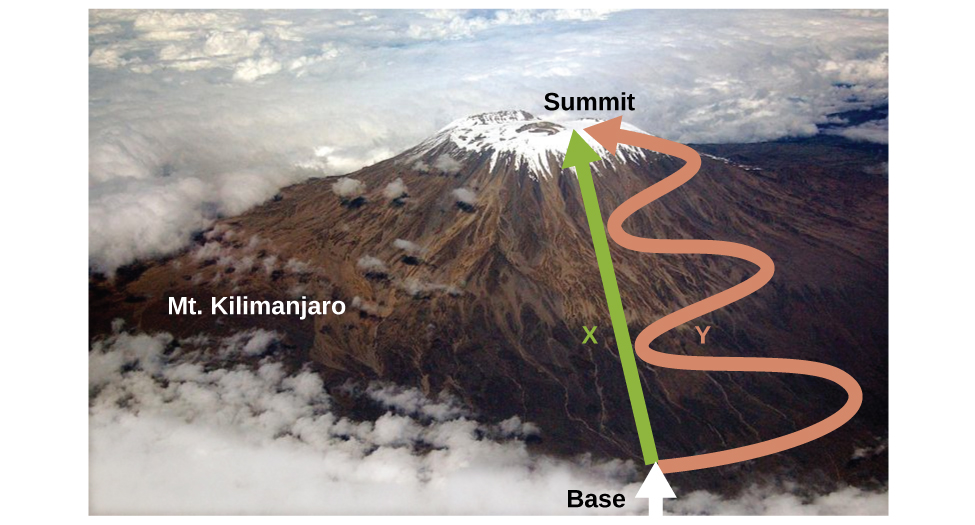
Internal energy is a type of quantity known as a state function (or state variable), whereas heat and work are not state functions. The value of a state function depends only on the state that a system is in, and not on how that state is reached, i.e. path-independent. If a quantity is not a state function, then its value does depend on how the state is reached, i.e. path-dependent. An example of a state function is altitude or elevation. If we stand on the summit of Mt. Kilimanjaro, we are at an altitude of 5895 m, and it does not matter whether we hiked there or parachuted there. The distance we travelled to the top of Kilimanjaro, however, is not a state function. We could climb to the summit by a direct route or by a more roundabout, circuitous path, Figure 4. The distances travelled would differ (distance is not a state function) but the elevation reached would be the same (altitude is a state function).
Example 1
A gas is enclosed in a vessel. The gas gains 62 J of heat and the vessel volume initially at 1.00 m3 contracts to 0.70 m3 at a constant pressure of 578 Pa. Find the
(a) work done on or done by the gas, and
(b) change in internal energy of the gas.
SOLUTION
(a) Apply Equation 1 to calculate work. The unit of pressure pascal is equal to newton per square metre.
[latex]\begin{align*} w &= -P\Delta V \\ &= -578 \text{ Pa}\left(0.70\text{ m}^3-1.00\text{ m}^3\right) \\ &= -587 \; \frac{\text{N}}{\text{m}^2}\left(0.70\text{ m}^3-1.00\text{ m}^3\right) \\ &=173 \text{ N m} = \boxed{173 \text{ J}}\end{align*}[/latex]
The work done on the gas is 173 J.
(b) Use Equation 2 to calculate the change in internal energy.
[latex]\begin{align*} \Delta U &= q + w \\ &= 62 \text{ J} + 173 \text{ J} \\ &= \boxed{+235 \text{ J}}\end{align*}[/latex]
The gas gains 235 J.
Example 2
A rigid vessel undergoes an internal energy change of −45 J. How much work is done on or by the vessel? How much heat is transferred to or from the vessel?
SOLUTION
A rigid vessel cannot expand or contract. The work involved is zero.
[latex]\begin{align*} w &= -P\Delta V \\ &= -P\cdot 0 \\ &= 0\end{align*}[/latex]
[latex]\begin{align*} \Delta U &= q + w \\ q &= \Delta U - w \\ &= \left(- 45 \text{ J}\right) - 0 \\ &= \boxed{-45 \text{ J}}\end{align*}[/latex]
From the vessel, 45 J of heat is transferred to the surroundings.
Optional Resource
Read an article to learn about how car engines work. The engine converts energy produced by the exothermic combustion reaction of a fuel such as gasoline into energy of motion.
The internal energy of a substance at a constant temperature and pressure is an extensive property that changes with amount of substance because:
A) The total potential energy stored in the chemical bonds increases as substance amount increases because there are “more total chemical bonds” in “more molecules of the substance”.
B) The total potential energy stored between molecules from intermolecular force interactions increases as substance amount increases because there are “more total intermolecular force interactions” between “more molecules of the substance”.
C) The total kinetic energy of the molecules increases as substance amount increases because there are “more molecules” with the “same average kinetic energy”.
D) All of the above are responsible for internal energy being an extensive property.
Click to see answer
D) All of the above are responsible for internal energy being an extensive property.

