Unit 5 Thermodynamics
5.2 Calorimetry
OpenStax
Section Learning Objectives
- Define heat capacity and specific heat capacity.
- Relate heat to the temperature change of a substance.
✓ SECTION 5.2 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion and videos. | No | 120 min |
| Optional Resource: Watch a video explanation about a bomb calorimeter. | No | 3 min |
| Optional Resource: Browse a web-based explanation about a bomb calorimeter and sample data. | No | 20 min |
| Optional Activity: Run a simulated calorimetry experiment. | No | 15 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 45 min |
📖 READING PORTION
Heat Capacity
Historically, energy was measured in units of calories (cal). A calorie is the amount of energy required to raise one gram of water by 1 degree C (1 kelvin). However, this quantity depends on the atmospheric pressure and the starting temperature of the water. The ease of measurement of energy changes in calories has meant that the calorie is still frequently used. The Calorie (with a capital C), or large calorie, commonly used in quantifying food energy content, is a kilocalorie. The SI unit of heat, work, and energy is the joule. A joule (J) is defined as the amount of energy used when a force of 1 newton moves an object 1 metre. It is named in honor of the English physicist James Prescott Joule. One joule is equivalent to 1 kg m2/s2, which is also called 1 newton–metre. A kilojoule (kJ) is 1000 joules. To standardize its definition, 1 calorie has been set to equal 4.184 joules.
Heat and temperature change are related. The heat capacity (C) of a body of matter is the quantity of heat (q) it absorbs or releases when it experiences a temperature change (ΔT) of 1 degree Celsius (or equivalently, 1 kelvin):
[latex]C = \frac{q}{\Delta T}[/latex]
Heat capacity is determined by both the type and amount of substance that absorbs or releases heat. It is therefore an extensive property—its value is proportional to the amount of the substance.
For example, consider the heat capacities of two cast iron frying pans, Figure 1. The heat capacity of the large pan is five times greater than that of the small pan because, although both are made of the same material, the mass of the large pan is five times greater than the mass of the small pan. More mass means more atoms are present in the larger pan, so it takes more energy to make all of those atoms vibrate faster. The heat capacity of the small cast iron frying pan is found by observing that it takes 18,150 J of energy to raise the temperature of the pan by 50.0 °C,
[latex]C_{\text{small pan}} = \frac{18,140 \;\text{J}}{50.0 \;^{\circ}\text{C}} = 363 \frac{\;\text{J}}{^\circ\text{C}}[/latex]
The larger cast iron frying pan, while made of the same substance, requires 90,700 J of energy to raise its temperature by 50.0 °C. The larger pan has a (proportionally) larger heat capacity because the larger amount of material requires a (proportionally) larger amount of energy to yield the same temperature change,
[latex]C_{\text{large pan}} = \frac{90,700 \;\text{J}}{50.0 \;^{\circ}\text{C}} = 1814 \frac{\;\text{J}}{^\circ\text{C}}[/latex]

The specific heat capacity (c, sometimes symbolized as cs) of a substance, commonly called its “specific heat,” is the quantity of heat required to raise the temperature of 1 gram of a substance by 1 degree Celsius (or 1 kelvin)
[latex]c = \frac{q}{m\Delta T}[/latex]
Specific heat capacity depends only on the kind of substance absorbing or releasing heat. It is an intensive property—the type, but not the amount, of the substance is all that matters. For example, the small cast iron frying pan has a mass of 808 g. The specific heat of iron (the material used to make the pan) is therefore
[latex]c_{\text{iron}} = \frac{18,140 \;\text{J}}{(808 \;\text{g})(50.0 \;^{\circ}\text{C})} = 0.449 \frac{\;\text{J}}{\text{g} \cdot \;^\circ\text{C}}[/latex]
The large frying pan has a mass of 4040 g. Using the data for this pan, we can also calculate the specific heat of iron
[latex]c_{\text{iron}} = \frac{90,700 \;\text{J}}{(4040 \;\text{g})(50.0 \;^{\circ}\text{C})} = 0.449 \frac{\;\text{J}}{\text{g} \cdot \;^\circ\text{C}}[/latex]
Although the large pan is more massive than the small pan, since both are made of the same material, they both yield the same value for specific heat (for the material of construction, iron). Note that specific heat is measured in units of energy per temperature per mass and is an intensive property, being derived from a ratio of two extensive properties (heat and mass). The molar heat capacity, also an intensive property, is the heat capacity per mole of a particular substance and has units of [latex]\frac{\text{J}}{\text{mol} \cdot °\text{C}}[/latex].
Liquid water has a relatively high specific heat (about 4.2 J/(g⋅°C)); most metals have much lower specific heats (usually less than 1 J/(g⋅°C)). The specific heat of a substance varies somewhat with temperature. However, this variation is usually small enough that we will treat specific heat as constant over the range of temperatures that will be considered in this course. Specific heats of some common substances are listed in Table 1.
|
Substance |
Symbol (state) |
Specific Heat, J/(g⋅°C) |
|
helium |
He(g) |
5.193 |
|
water |
H2O(l) |
4.184 |
|
ethanol |
C2H6O(l) |
2.376 |
|
ice |
H2O(s) |
2.093 (at −10 °C) |
|
water vapor |
H2O(g) |
1.864 |
|
nitrogen |
N2(g) |
1.040 |
|
oxygen |
O2(g) |
0.918 |
|
aluminum |
Al(s) |
0.897 |
|
carbon dioxide |
CO2(g) |
0.853 |
|
argon |
Ar(g) |
0.522 |
|
iron |
Fe(s) |
0.449 |
|
copper |
Cu(s) |
0.385 |
|
lead |
Pb(s) |
0.130 |
|
gold |
Au(s) |
0.129 |
|
silicon |
Si(s) |
0.712 |
|
Table 1 Specific Heats of Common Substances at 25 °C and 1 bar. Source: OpenStax Chemistry 2e |
||
If we know the mass of a substance and its specific heat, we can determine the amount of heat, q, entering or leaving the substance by measuring the temperature change before and after the heat is gained or lost:
Equation 1
[latex]\begin{array} {r @{{}={}} l} q &= \text{(specific heat)} \times \text{(mass of substance)} \times \text{(temperature change)} \\[1em] q &= c \times m \times \Delta T =c \times m \times (T_{\text{final}} - T_{\text{initial}}) \end{array}[/latex]
- [latex]c[/latex], specific heat of the substance ([latex]\frac{\text{J}}{\text{g}\cdot^\circ \text{C}}[/latex])
- [latex]m[/latex], mass of substance ([latex]\text{g}[/latex])
- [latex]\Delta T[/latex], temperature change ([latex]^\circ \text{C}[/latex]), also expressed as [latex]T_\text{final} – T_\text{initial}[/latex]
If a substance gains thermal energy, its temperature increases, its final temperature is higher than its initial temperature, [latex]T_\text{final} – T_\text{initial}[/latex] has a positive value, and the value of q is positive. If a substance loses thermal energy, its temperature decreases, the final temperature is lower than the initial temperature, [latex]T_\text{final} – T_\text{initial}[/latex] has a negative value, and the value of q is negative.
Example 1
Measuring Heat
A flask containing 8.0 × 102 g of water is heated, and the temperature of the water increases from 21 °C to 85 °C. How much heat did the water absorb?
SOLUTION
To answer this question, consider these factors:
the specific heat of the substance being heated (in this case, water)
the amount of substance being heated (in this case, 800 g)
the magnitude of the temperature change (in this case, from 21 °C to 85 °C).
The specific heat of water is 4.184 J/(g⋅°C), so to heat 1 g of water by 1 °C requires 4.184 J. We note that since 4.184 J is required to heat 1 g of water by 1 °C, we will need 800 times as much to heat 800 g of water by 1 °C. Finally, we observe that since 4.184 J are required to heat 1 g of water by 1 °C, we will need 64 times as much to heat it by 64 °C (that is, from 21 °C to 85 °C).
This can be summarized using the equation:
[latex]\begin{array} {r@ {{}={}} l} q &= c \times m \times \Delta T = c \times m \times (T_{\text{final}} - T_{\text{initial}}) \\[1em] &= (4.184 \;\text{J/}\rule[0.25ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{g} \;^\circ\text{C} \times (800 \;\rule[0.25ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{g}) \times (85 - 20) \;^\circ\text{C} \\[1em] &= (4.184 \;\text{J/}\rule[0.25ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{g} \;^\circ\rule[0.5ex]{0.75em}{0.1ex}\hspace{-0.75em}\text{C} \times (800 \;\rule[0.25ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{g}) \times (65) \;^\circ\rule[0.5ex]{0.75em}{0.1ex}\hspace{-0.75em}\text{C} \\[1em] & \boxed{210,000 \;\text{J}} \text{ }(= 210 \;\text{kJ}) \end{array}[/latex]
Because the temperature increased, the water absorbed heat and q is positive.
Example 2
How much heat in kilojoules is required to raise the temperature of 237 g of cold water from 4.0 °C to 37.0 °C?
SOLUTION
qwater = +32.7 kJ
Having trouble figuring out this problem? Consult the following video:
Video 1 Heat and Heat Capacity Problem Solving Example (8 min 3 s).
Measuring Heat by Calorimetry
One technique we can use to measure the amount of heat involved in a chemical or physical process is known as calorimetry. Calorimetry is used to measure amounts of heat transferred to or from a substance. To do so, the heat is exchanged with a calibrated object (calorimeter). The change in temperature of the measuring part of the calorimeter is converted into the amount of heat (since the previous calibration was used to establish its heat capacity). The measurement of heat transfer using this approach requires the definition of a system (the substance or substances undergoing the chemical or physical change) and its surroundings (the other components of the measurement apparatus that serve to either provide heat to the system or absorb heat from the system). Knowledge of the heat capacity of the surroundings, and careful measurements of the masses of the system and surroundings and their temperatures before and after the process allows one to calculate the heat transferred.
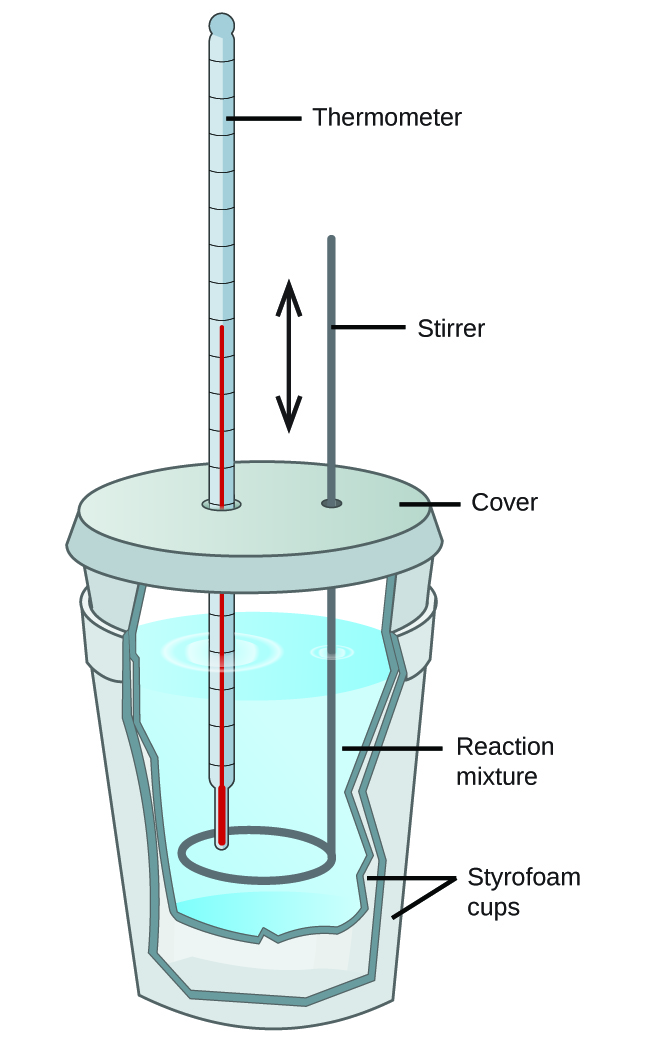
A calorimeter is a device used to measure the amount of heat involved in a chemical or physical process. For example, when an exothermic reaction occurs in solution in a calorimeter, the heat produced by the reaction is absorbed by the solution, which increases its temperature. When an endothermic reaction occurs, the heat required is absorbed from the thermal energy of the solution, which decreases its temperature. The temperature change, along with the specific heat and mass of the solution, can then be used to calculate the amount of heat involved in either case.
Scientists use well-insulated calorimeters that all but prevent the transfer of heat between the calorimeter and its environment, which effectively limits the “surroundings” to the nonsystem components with the calorimeter (and the calorimeter itself). This enables the accurate determination of the heat involved in chemical processes, the energy content of foods, and so on. General chemistry students often use simple calorimeters constructed from polystyrene cups, Figure 2. These easy-to-use “coffee cup” calorimeters allow more heat exchange with the outside environment, and therefore produce less accurate energy values.
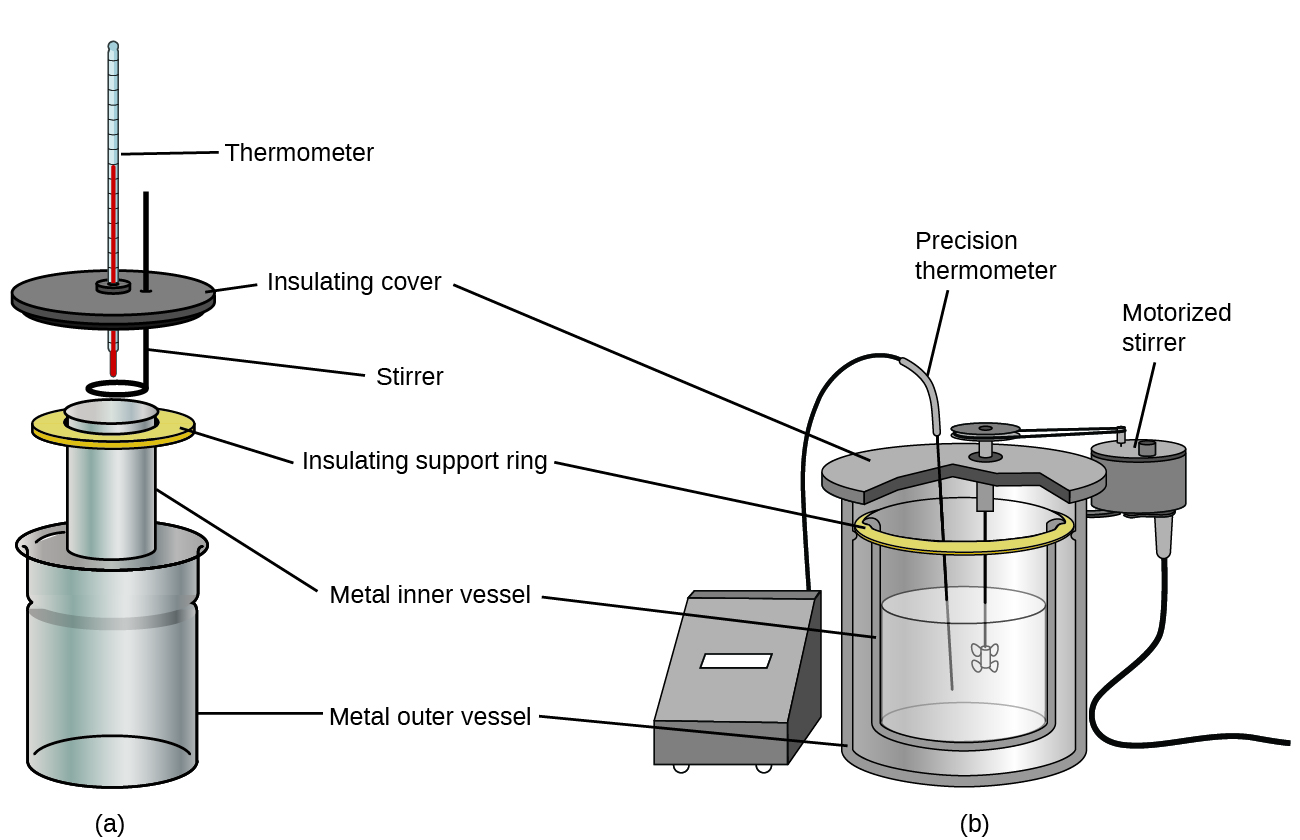
Commercial solution calorimeters are also available. Relatively inexpensive calorimeters often consist of two thin-walled cups that are nested in a way that minimizes thermal contact during use, along with an insulated cover, handheld stirrer, and simple thermometer. More expensive calorimeters used for industry and research typically have a well-insulated, fully enclosed reaction vessel, motorized stirring mechanism, and a more accurate temperature sensor, Figure 3.
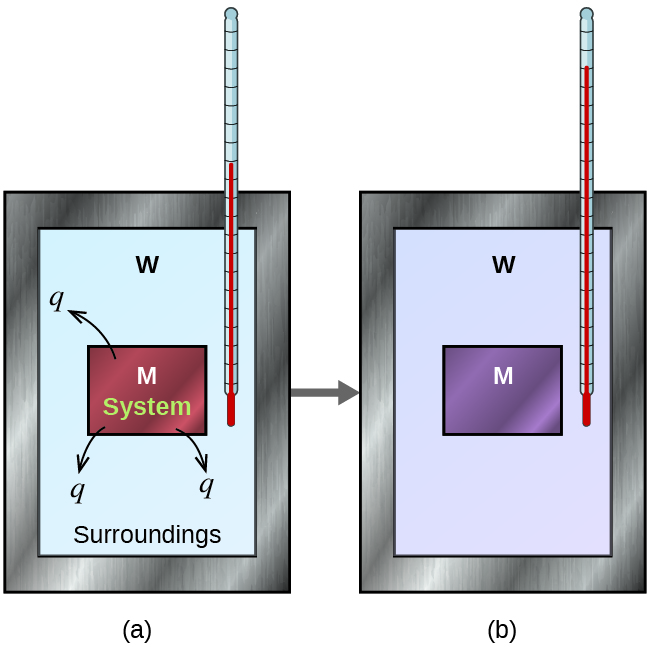
Before we practice calorimetry problems involving chemical reactions, consider a simpler example that illustrates the core idea behind calorimetry. Suppose we initially have a high-temperature substance, such as a hot piece of metal (M), and a low-temperature substance, such as cool water (W). If we place the metal in the water, heat will flow from M to W. The temperature of M will decrease, and the temperature of W will increase, until the two substances have the same temperature—that is, when they reach thermal equilibrium, Figure 4. If this occurs in a calorimeter, ideally all of this heat transfer occurs between the two substances, with no heat gained or lost by either the calorimeter or the calorimeter’s surroundings. Under these ideal circumstances, the net heat change is zero:
[latex]q_{\text{substance M}} + q_\text{substance W} = 0[/latex]
This relationship can be rearranged to show that the heat gained by substance M is equal to the heat lost by substance W
[latex]q_{\text{substance M}} = - q_{\text{substance W}}[/latex]
The magnitude of the heat (change) is therefore the same for both substances, and the negative sign merely shows that [latex]q_\text{substance M}[/latex] and [latex]q_\text{substance W}[/latex] are opposite in direction of heat flow (gain or loss) but does not indicate the arithmetic sign of either q value (that is determined by whether the matter in question gains or loses heat, per definition). In the specific situation described, [latex]q_\text{substance M}[/latex] is a negative value and [latex]q_\text{substance W}[/latex] is positive, since heat is transferred from M to W.
Example 3
Heat Transfer between Substances at Different Temperatures
A 360-g piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 mL of water at 24.0 °C. The final temperature of the water was measured as 42.7 °C. Calculate the initial temperature of the piece of rebar. Assume the specific heat of steel is approximately the same as that for iron, and that all heat transfer occurs between the rebar and the water (there is no heat exchange with anything else).
SOLUTION
The temperature of the water increases from 24.0 °C to 42.7 °C, so the water absorbs heat. That heat came from the piece of rebar, which initially was at a higher temperature. Assuming that all heat transfer was between the rebar and the water, with no heat “lost” to anything else, then heat given off by rebar = −heat taken in by water, or:
[latex]q_{\text{rebar}} = -q_{\text{water}}[/latex]
Since we know how heat is related to other measurable quantities, we have:
[latex](c \times m \times \Delta T)_{\text{rebar}} = -(c \times m \times \Delta T)_{\text{water}}[/latex]
Letting f = final and i = initial, in expanded form, this becomes:
[latex]c_{\text{rebar}} \times m_{\text{rebar}} \times (T_{\text{f, rebar}} - T_{\text{i, rebar}}) = -c_{\text{water}} \times m_{\text{water}} \times (T_{\text{f, water}} - T_{\text{i, water}})[/latex]
The density of water is 1.0 g/mL, so 425 mL of water = 425 g. Noting that the final temperature of both the rebar and water is 42.7 °C, substituting known values yields:
[latex](0.449 \;\text{J/g} \;^\circ\text{C})(360 \;\text{g})(42.7 \;^\circ\text{C} - T_{\text{i, rebar}}) = -(4.184 \;\text{J/g} \;^\circ\text{C})(425 \;\text{g})(42.7 \;^\circ\text{C} - 24.0 \;^\circ\text{C})[/latex]
[latex]T_{\text{i, rebar}} = \frac{(4.184 \;\text{J/g} \;^\circ\text{C})(425 \;\text{g})(42.7 \;^\circ\text{C} - 24.0 \;^\circ\text{C})}{(0.449 \;\text{J/g} \;^\circ\text{C})(360 \;\text{g})} + 42.7 \;^\circ\text{C}[/latex]
Solving this gives Ti, rebar= 248 °C, so the initial temperature of the rebar was 248 °C.
Example 4
A 100.0 g copper sample at 100.0 °C is added to 50.0 g of water at 26.5 °C. What is the final temperature of the copper/water mixture? For this problem assume the specific heat capacity for water is 4.184 J mol−1 °C−1 and the specific heat capacity for copper is 0.385 J mol−1 °C−1.
SOLUTION
Tfinal = 37.9 °C
Having trouble figuring out this problem? Consult the following video:
Video 2 Thermal Energy Transfer Problem Solving Example (18 min 16 s).
This method can also be used to determine other quantities, such as the specific heat of an unknown metal.
Example 5
Identifying a Metal by Measuring Specific Heat
A 59.7 g piece of metal that had been submerged in boiling water was quickly transferred into 60.0 mL of water initially at 22.0 °C. The final temperature is 28.5 °C. Use these data to determine the specific heat of the metal. Use this result to identify the metal.
SOLUTION
Assuming perfect heat transfer, heat given off by metal = −heat taken in by water, or:
[latex]q_{\text{metal}} = -q_{\text{water}}[/latex]
In expanded form, this is:
[latex]c_{\text{metal}} \times m_{\text{metal}} \times (T_{\text{f, metal}} - T_{\text{i, metal}}) = -c_{\text{water}} \times m_{\text{water}} \times (T_{\text{f, water}} - T_{\text{i, water}})[/latex]
Noting that since the metal was submerged in boiling water, its initial temperature was 100.0 °C; and that for water, 60.0 mL = 60.0 g; we have:
[latex](c_{\text{metal}}) (59.7 \;\text{g}) (28.5 \;^\circ\text{C} - 100.0 \;^\circ\text{C}) = -(4.184 \;\text{J/g} \;^\circ\text{C})(60.0 \;\text{g})(28.5 \;^\circ\text{C} - 22.0 \;^\circ\text{C})[/latex]
Solving this:
[latex]c_{\text{metal}} = \frac{-(4.184 \;\text{J/g} \;^\circ\text{C})(60.0 \;\text{g})(6.5 \;^\circ\text{C})}{(59.7 \;\text{g})(-71.5 \;^\circ\text{C})} = 0.38 \;\text{J/g} \;^\circ \text{C}[/latex]
Comparing this with values in Table 1, our experimental specific heat is closest to the value for copper (0.39 J/(g⋅°C)), so we identify the metal as copper.
When we use calorimetry to determine the heat involved in a chemical reaction, the same principles we have been discussing apply. The amount of heat absorbed by the calorimeter is often small enough that we can neglect it (though not for highly accurate measurements, as discussed later), and the calorimeter minimizes energy exchange with the surroundings. Because energy is neither created nor destroyed during a chemical reaction, there is no overall energy change during the reaction. The heat produced or consumed in the reaction (the “system”), qreaction, plus the heat absorbed or lost by the solution (the “surroundings”), qsolution, must add up to zero:
[latex]q_{\text{reaction}} + q_{\text{solution}} = 0[/latex]
This means that the amount of heat produced or consumed in the reaction equals the amount of heat absorbed or lost by the solution:
[latex]q_{\text{reaction}} = -q_{\text{solution}}[/latex]
This concept lies at the heart of all calorimetry problems and calculations.
Example 6
Heat Produced by an Exothermic Reaction
When 50.0 mL of 1.00 M HCl(aq) and 50.0 mL of 1.00 M NaOH(aq), both at 22.0 °C, are added to a coffee cup calorimeter, the temperature of the mixture reaches a maximum of 28.9 °C. What is the approximate amount of heat produced by this reaction?
[latex]\text{HCl}(aq) + \text{NaOH}(aq) \longrightarrow \text{NaCl}(aq) + \text{H}_2 \text{O}(l)[/latex]
SOLUTION
To visualize what is going on, imagine that we could combine the two solutions so quickly that no reaction took place while they mixed; then after mixing, the reaction took place. At the instant of mixing, you have 100.0 mL of a mixture of HCl and NaOH at 22.0 °C. The HCl and NaOH then react until the solution temperature reaches 28.9 °C. The heat given off by the reaction is equal to that taken in by the solution.
[latex]q_{\text{reaction}} = -q_{\text{solution}}[/latex]
It is important to remember that this relationship only holds if the calorimeter does not absorb any heat from the reaction, and there is no heat exchange between the calorimeter and its surroundings. Next, we know that the heat absorbed by the solution depends on its specific heat, mass, and temperature change.
[latex]q_{\text{solution}} = (c \times m \times \Delta T)_{\text{solution}}[/latex]
To proceed with this calculation, we need to make a few more reasonable assumptions or approximations. Since the solution is aqueous, we can proceed as if it were water in terms of its specific heat and mass values. The density of water is approximately 1.0 g/mL, so 100.0 mL has a mass of about 1.0 × 102 g (two significant figures). The specific heat of water is approximately 4.184 J/(g⋅°C), so we use that for the specific heat of the solution. Substituting these values gives
[latex]q_{\text{solution}} = (4.184 \;\text{J/g} \;^\circ\text{C})(1.0 \times 10^2 \;\text{g})(28.9 \;^\circ\text{C} - 22.0 \;^\circ\text{C}) = 2.89 \times 10^3 \;\text{J}[/latex]
Finally, since we are trying to find the heat of the reaction, we have
[latex]q_{\text{reaction}} = -q_{\text{solution}} = \boxed{-2.89 \times 10^3 \;\text{J}}[/latex]
The negative sign indicates that the reaction is exothermic and produces 2.89 kJ of heat.
Example 7
Heat Flow in an Instant Ice Pack
When solid ammonium nitrate dissolves in water, the solution becomes cold. This is the basis for an “instant ice pack”. When 3.21 g of solid NH4NO3 dissolves in 50.0 g of water at 24.9 °C in a calorimeter, the temperature decreases to 20.3 °C.
Calculate the value of q for this reaction and explain the meaning of its arithmetic sign. State any assumptions that you made.
SOLUTION
We assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself), in which case
[latex]q_{\text{rxn}} = -q_{\text{soln}}[/latex]
with “rxn” and “soln” used as shorthand for “reaction” and “solution,” respectively.
Assuming also that the specific heat of the solution is the same as that for water, we have
[latex]\begin{array}{r @{{}={}} l} q_{\text{rxn}} &= -{q_{\text{soln}}} = -(c \times m \times \Delta T)_{\text{soln}} \\[1em] &= -[(4.184 \;\text{J/g} \;^\circ\text{C}) \times (53.2 \;\text{g}) \times (20.3 \;^\circ\text{C} - 24.9 \;^\circ\text{C})] \\[1em] &= -[(4.184 \;\text{J/g} \;^\circ\text{C}) \times (53.2 \;\text{g}) \times (-4.6 \;^\circ\text{C})] \\[1em] &= + 1.0 \times 10^3 \;\text{J} = \boxed{+1.0 \;\text{kJ}} \end{array}[/latex]
The positive sign for q indicates that the dissolution is an endothermic process.
If the amount of heat absorbed by a calorimeter is too large to neglect or if we require more accurate results, then we must take into account the heat absorbed both by the solution and by the calorimeter. The calorimeters described are designed to operate at constant (atmospheric) pressure and are convenient to measure heat flow accompanying processes that occur in solution. A different type of calorimeter that operates at constant volume, colloquially known as a bomb calorimeter, is used to measure the energy produced by reactions that yield large amounts of heat and gaseous products, such as combustion reactions. (The term “bomb” comes from the observation that these reactions can be vigorous enough to resemble explosions that would damage other calorimeters.) This type of calorimeter consists of a robust steel container (the “bomb”) that contains the reactants and is itself submerged in water. The sample is placed in the bomb, which is then filled with oxygen at high pressure. A small electrical spark is used to ignite the sample. The energy produced by the reaction is trapped in the steel bomb and the surrounding water. The temperature increase is measured and, along with the known heat capacity of the calorimeter, is used to calculate the energy produced by the reaction. Bomb calorimeters require calibration to determine the heat capacity of the calorimeter and ensure accurate results. The calibration is accomplished using a reaction with a known q, such as a measured quantity of benzoic acid ignited by a spark from a nickel fuse wire that is weighed before and after the reaction. The temperature change produced by the known reaction is used to determine the heat capacity of the calorimeter. The calibration is generally performed each time before the calorimeter is used to gather research data.
Example 8
Bomb Calorimetry
When 3.12 g of glucose, C6H12O6, is burned in a bomb calorimeter, the temperature of the calorimeter increases from 23.8 °C to 35.6 °C. The heat capacity of the bomb, without water, is 893 J/°C. The calorimeter contains 775 g of water. How much heat was produced by the combustion of the glucose sample?
SOLUTION
The combustion produces heat that is primarily absorbed by the water and the bomb. (The amounts of heat absorbed by the reaction products and the unreacted excess oxygen are relatively small and dealing with them is beyond the scope of this course. We will neglect them in our calculations.)
The heat produced by the reaction is absorbed by the water and the bomb
[latex]\begin{array}{r @{{}={}} l} q_{\text{rxn}} &= -({q_{\text{water}} + q_{\text{bomb}}}) \\[1em] &= -[(4.184 \;\text{J/g} \;^\circ\text{C}) \times (775 \;\text{g}) \times (35.6 \;^\circ\text{C} - 23.8 \;^\circ\text{C}) + 893\;\text{J/}^\circ\text{C} \times (35.6 \;^\circ\text{C} - 23.8 \;^\circ\text{C})] \\[1em] &= -(38,300 \;\text{J} + 10,500 \;\text{J}) \\[1em] &= -48,800 \;\text{J} = \boxed{-48.8 \;\text{kJ}} \end{array}[/latex]
This reaction released 48.8 kJ of heat when 3.12 g of glucose was burned.
The heat given off when we operate a Bunsen burner is equal to the enthalpy change (ΔH, Section 5.3) of the methane combustion reaction that takes place, since it occurs at the essentially constant pressure of the atmosphere. On the other hand, the heat produced by a reaction measured in a bomb calorimeter is not equal to ΔH because the closed, constant-volume metal container prevents expansion work from occurring. The heat is equal to ΔU. From Section 5.1, we saw that
[latex]\Delta U = q + w[/latex]
When there is no pressure-volume work, [latex]w = 0[/latex], Hence
Equation 2
[latex]\Delta U = q[/latex] (at constant volume)
- [latex]\Delta U[/latex], change in internal energy ([latex]\text{J}[/latex])
- [latex]q[/latex], heat ([latex]\text{J}[/latex])
Example 9
The combustion of 1.013 g of vanillin, C8H8O3, in a bomb calorimeter where the total heat capacity of the calorimeter, bomb and water together, is 4.90 kJ °C−1 results in a temperature rise of the calorimeter contents from 24.89 to 30.09 °C. What is the molar heat of combustion (which will also be the molar change in internal energy ΔrU of combustion) of vanillin in kJ mol−1? The molar mass of vanillin is 152.147 g mol−1.
SOLUTION
qrxn = ΔrU = −3.83 × 103 kJ mol−1
Having trouble figuring out this problem? Consult the following video:
Video 3 Bomb Calorimetry Problem Solving Example (13 min 49 s).
Chemistry in Real Life
ᖁᓪᓕᖅ Oil lamps

The Arctic tundra is a desert and some nights have over 24 hours of darkness. Where there is no wood for heating and lighting, Inuit people use a traditional oil lamp called ᖁᓪᓕᖅ (qulliq). There are multiple ways to construct the qulliq, and a common design has a soapstone dish (Figure 5) containing seal oil as fuel and is lit at the edge of the dish; whale oil is another fuel. Agriculture is not possible in the Arctic; thus, seal is a food staple for Inuit people.
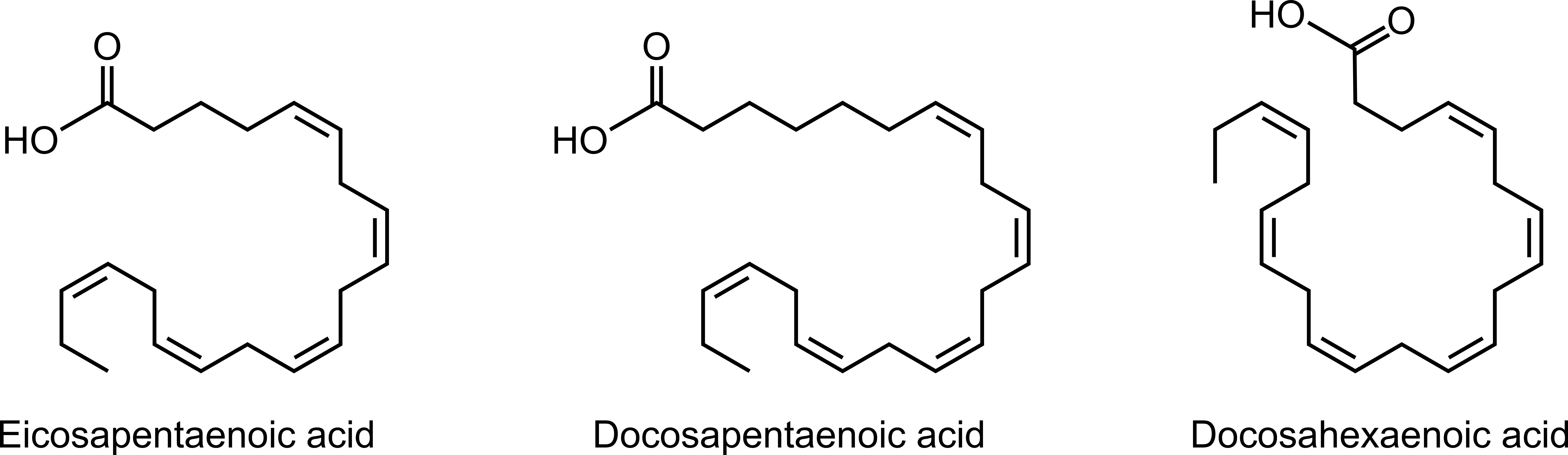
Seal blubber is analogous to gasoline as fuel because both are mixtures of hydrocarbons. Gasoline is a mixture of C4-C12 alkanes, alkenes, and cycloalkanes. The hydrocarbons in seal blubber are fatty acids. Fatty acids are carboxylic acids with a long hydrocarbon chain that may be saturated, monounsaturated (has one C=C double bond), or polyunsaturated (has multiple C=C double bonds). Blubber from seal species Cystophora cristata and Phagophilus groenlandicus consists of all three types of fatty acids.1 Examples of polyunsaturated fatty acids in seal blubber are eicosapentaenoic acid, docosapentaenoic acid, and docosahexaenoic acid (Figure 6). Eicosapentaenoic and docosahexaenoic are also found in fish and are marketed as omega-3 supplements.
The energy output from the qulliq is adjustable to meet the demands of cooking food, drying wet clothes, melting ice, boiling water, and keeping the dwelling place warm while sleeping. Just as electrical appliances are necessities for many families, the versatility of the qulliq is amenable to meeting all these needs. Beyond the utilitarian value, lighting and tending the qulliq is a way for Inuit women to teach culture and tradition from one generation to another.2 Watch a qulliq demonstration in Video 4.
Video 4 Lighting of Qulliq (5 min 37 s).
1Linn Anne Brunborg, Kåre Julshamn, Ragnar Nortvedt, Livar Frøyland (2006) Nutritional composition of blubber and meat of hooded seal (Cystophora cristata) and harp seal (Phagophilus groenlandicus) from Greenland. Food Chemistry 96:524-531.
2https://uwaterloo.ca/chem13-news-magazine/fall-2022-special-edition/feature/land-beneath-our-feet
Optional Resources
♦ Watch a video explanation of a bomb calorimeter.
Video 5 Physical Chemistry iBook – Bomb Calorimetry (2 min 45 s).
Optional Activity
A 45-g aluminum spoon (specific heat 0.88 J/(g⋅°C)) at 24°C is placed in 180 mL (180 g) of coffee at 85°C and the temperature of the two become equal. What is the final temperature when the two become equal? Assume that coffee has the same specific heat as water, 4.184 J/(g⋅°C).
Click to see answer
[latex]\begin{eqnarray} (cm\Delta T)_{\text{spoon}}&=&-(cm\Delta T)_{\text{coffee}} \\ (45 \text{ g})\left(0.88 \frac{\text{J}}{\text{g} ^\circ \text{C}}\right)(T_{\text{f}}–24)^\circ \text{C} &=& –(180 \text{ g})\left(4.184 \frac{\text{ J}}{\text{g} ^\circ \text{C}}\right)(T_\text{f}–85) ^\circ \text{C} \\ 39.6T_{\text{f}} – 950.4 \text{ J} &=& –753.1T_{\text{f}} + 64015.2 \text{ J} \\ T_{\text{f}} &=& \boxed{82.0 ^\circ \text{C}} \end{eqnarray}[/latex]

