Unit 5 Thermodynamics
5.3 Enthalpy
OpenStax
Section Learning Objectives
- Define enthalpy and relate enthalpy to stoichiometry.
- Explain the energy differences between solid, liquid, and gas states of a substance.
- Define enthalpy of formation and enthalpy of combustion.
✓ SECTION 5.3 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion and video. | No | 60 min |
| Optional Resource: Watch a video explanation about phase changes. | No | 5 min |
| Optional Resource: Watch a video of iodine undergoing phase transition. | No | 2 min |
| Optional Activity: Explore a simulation on particle motion. | No | 5 min |
| Optional Activity: Simulate a calorimetry experiment involving enthalpy of solution. | No | 20 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 30 min |
📖 READING PORTION
Chemists ordinarily use a property known as enthalpy (H) to describe the thermodynamics of chemical and physical processes. Enthalpy is also called latent heat. At constant external pressure with q = ΔH, enthalpy is the most convenient choice for determining heat. Enthalpy is defined as the sum of a system’s internal energy (U) and the mathematical product of its pressure (P) and volume (V)
[latex]H = U + PV[/latex]
Derivation of the equation, q = ΔH:
Since enthalpy is derived from three state functions (U, P, and V), enthalpy is also a state function. In this chemistry course, enthalpy values for specific substances are not measured directly; only enthalpy changes for chemical or physical processes are determined
[latex]\Delta H = \Delta U + (\Delta P)V + P(\Delta V)[/latex]
For processes that take place at constant pressure (a common condition for many chemical and physical changes), ΔP = 0, hence (ΔP)V = 0. Moreover, the mathematical product PΔV represents work (w), namely, expansion or pressure-volume work. By their definitions, the arithmetic signs of ΔV and w will always be opposite
[latex]P \Delta V = -w[/latex]
Substituting work and the definition of internal energy into the enthalpy-change equation yields
[latex]\begin{array} {r @{{}={}} l} \Delta H &= \Delta U + P \Delta V \\[1em] &= q + w - w \\[1em] &= q \end{array}[/latex]
Equation 1
[latex]\Delta H = q[/latex] (at constant pressure)
- [latex]\Delta H[/latex], enthalpy change ([latex]\text{J}[/latex])
- [latex]q[/latex], heat ([latex]\text{J}[/latex])
If a chemical or physical process is carried out at constant pressure with the only work done caused by expansion or contraction, then the heat flow (q) and enthalpy change (ΔH) for the process are equal. Note that some textbooks use the notation qp to specify heat flow at constant pressure and distinguish from qv, heat flow at constant volume. Because CHEM 1523 mostly involves constant pressure, most heat flow is assumed at constant pressure (q = qp).
In CHEM 1523, we are taking a more simplistic view of thermodynamics. For higher level courses in physical chemistry and chemical engineering, we may actually define a value for enthalpy and discuss changes occurring at constant volume.
The following conventions apply when we use ΔH:
-
-
Chemists use a thermochemical equation to represent the changes in both matter and energy. In a thermochemical equation, the enthalpy change of a reaction is shown as a ΔH value following the equation for the reaction. This ΔH value indicates the amount of heat associated with the reaction involving the number of moles of reactants and products as shown in the chemical equation. For example, consider this equation:
[latex]\text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{H}_2 \text{O} (l) \;\; \Delta H = -286 \;\text{kJ}[/latex]
This equation indicates that when 1 mole of hydrogen gas and [latex]\frac{1}{2}[/latex] mole of oxygen gas at some temperature and pressure change to 1 mole of liquid water at the same temperature and pressure, 286 kJ of heat are released to the surroundings. If the coefficients of the chemical equation are multiplied by some factor, the enthalpy change must be multiplied by that same factor (ΔH is an extensive property),
[latex]\begin{array}{l l} (\text{two-fold increase in amounts}) \\ 2 \text{H}_2(g) + \text{O}_2(g) \longrightarrow 2 \text{H}_2 \text{O}(l) & \Delta H = 2 \times (-286 \;\text{kJ}) = -572 \;\text{kJ} \\[1em] (\text{two-fold decrease in amounts}) \\ \frac{1}{2} \text{H}_2(g) + \frac{1}{4} \text{O}_2(g) \longrightarrow \frac{1}{2} \text{H}_2 \text{O}(l) & \Delta H = \frac{1}{2} \times (-286 \;\text{kJ}) = -143 \;\text{kJ} \end{array}[/latex]
-
The enthalpy change of a reaction depends on the physical state of the reactants and products of the reaction (whether we have gases, liquids, solids, or aqueous solutions), so these must be shown. For example, when 1 mole of hydrogen gas and [latex]\frac{1}{2}[/latex] mole of oxygen gas change to 1 mole of liquid water at the same temperature and pressure, 286 kJ of heat are released. If gaseous water forms, only 242 kJ of heat are released.
[latex]\text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{H}_2 \text{O}(g) \;\;\;\;\; \Delta H = -242 \;\text{kJ}[/latex]
-
A negative value of an enthalpy change, ΔH, indicates an exothermic reaction; a positive value of ΔH indicates an endothermic reaction. If the direction of a chemical equation is reversed, the arithmetic sign of its ΔH is changed (a process that is endothermic in one direction is exothermic in the opposite direction).
-
Example 1
Measurement of an Enthalpy Change
When 0.0500 mol of HCl(aq) reacts with 0.0500 mol of NaOH(aq) to form 0.0500 mol of NaCl(aq), 2.9 kJ of heat are produced. What is ΔH, the enthalpy change, per mole of acid reacting?
[latex]\text{HCl}(aq) + \text{NaOH}(aq) \longrightarrow \text{NaCl}(aq) + \text{H}_2 \text{O}(l)[/latex]
SOLUTION
For the reaction of 0.0500 mol acid (HCl), q = −2.9 kJ. This ratio [latex]\frac{-2.9 \;\text{kJ}}{0.0500 \;\text{mol HCl}}[/latex] can be used as a conversion factor to find the heat produced when 1 mole of HCl reacts:
[latex]\Delta H = 1 \;\rule[0.5ex]{3.7em}{0.1ex}\hspace{-3.7em}\text{mol HCl} \times \frac{-2.9 \;\text{kJ}}{0.0500 \;\rule[0.5ex]{2.8em}{0.1ex}\hspace{-2.8em}\text{mol HCl}} = \boxed{-58 \;\text{kJ}}[/latex]
The enthalpy change when 1 mole of HCl reacts is −58 kJ. Since that is the number of moles in the chemical equation, we write the thermochemical equation as:
[latex]\text{HCl}(aq) + \text{NaOH}(aq) \longrightarrow \text{NaCl}(aq) + \text{H}_2 \text{O}(l) \;\;\;\;\; \Delta H = -58 \;\text{kJ}[/latex]
Be sure to take both stoichiometry and limiting reactants into account when determining the ΔH for a chemical reaction.
Example 2
Another Example of the Measurement of an Enthalpy Change
A gummy bear contains 2.67 g sucrose, C12H22O11. When it reacts with 7.19 g potassium chlorate, KClO3, 43.7 kJ of heat are produced. Determine the enthalpy change for the reaction
[latex]\text{C}_{12} \text{H}_{22} \text{O}_{11}(aq) + 8\text{KClO}_3(aq) \longrightarrow 12\text{CO}_{2}(g) + 11\text{H}_{2} \text{O}(l) + 8\text{KCl}(aq)[/latex].
SOLUTION
We have [latex]2.67 \;\rule[0.5ex]{0.3em}{0.1ex}\hspace{-0.3em}\text{g} \times \frac{1 \;\text{mol}}{342.3 \;\rule[0.25ex]{0.55em}{0.1ex}\hspace{-0.55em}\text{g}} = 0.00780 \;\text{mol C}_{12} \text{H}_{22} \text{O}_{11}[/latex] available, and [latex]7.19 \;\rule[0.5ex]{0.6em}{0.1ex}\hspace{-0.6em}\text{g} \times \frac{1 \;\text{mol}}{122.5 \;\rule[0.25ex]{0.55em}{0.1ex}\hspace{-0.55em}\text{g}} = 0.0587 \;\text{mol KClO}_3[/latex] available. Since [latex]0.0587 \;\text{mol KClO}_3 \times \frac{1 \;\text{mol C}_{12} \text{H}_{22} \text{O}_{11}}{8 \;\text{mol KClO}_3} = 0.00734 \;\text{mol C}_{12} \text{H}_{22} \text{O}_{11}[/latex] is needed, C12H22O11 is the excess reactant and KClO3 is the limiting reactant.
The reaction uses 8 mol KClO3, and the conversion factor is [latex]\frac{-43.7 \;\text{kJ}}{0.0587 \;\text{mol KClO}_3}[/latex], so we have [latex]\Delta H = 8 \;\text{mol} \times \frac{-43.7 \;\text{kJ}}{0.0587 \;\text{mol KClO}_3} = \boxed{-5960 \;\text{kJ}}[/latex]. The enthalpy change for this reaction is −5960 kJ, and the thermochemical equation is
[latex]\text{C}_{12} \text{H}_{22} \text{O}_{11} + 8\text{KClO}_3 \longrightarrow 12\text{CO}_{2} + 11\text{H}_{2} \text{O} + 8\text{KCl} \;\;\;\;\; \Delta H = -5960 \;\text{ kJ}[/latex]
Molar Enthalpy Change
Since the enthalpy change for a given reaction is proportional to the amounts of substances involved, enthalpy change may be reported as the ΔH per amount of substance. Note that this is similar to reporting the heat capacity of a substance per mass of substance to get the specific heat capacity, Section 5.2. Enthalpy change is often expressed in units of energy, such as joules or kilojoules, but dividing the amount of energy by moles gives units of joules per mole (J/mol) or kilojoules per mole (kJ/mol). The inclusion of a subscript “r” in the ΔH notation, as in ΔHr, denotes the molar enthalpy change for a particular reaction. The molar enthalpy change of a reaction can also be symbolized as ΔrH. From the example, we saw that the reaction
[latex]\text{C}_{12} \text{H}_{22} \text{O}_{11}(aq) + 8\text{KClO}_3(aq) \longrightarrow 12\text{CO}_{2}(g) + 11\text{H}_{2} \text{O}(l) + 8\text{KCl}(aq)[/latex]
has the enthalpy change ΔH = −5960 kJ. The molar enthalpy change per mole of reaction is
[latex]\Delta H_{\text{r}}=−5960 \text{ kJ/mol}[/latex] or [latex]\Delta H_{\text{r}}=−5960 \text{ kJ/mol rxn}[/latex]
The unit “mol rxn” refers to the instance the particular reaction occurs with the indicated stoichiometry. Here 5960 kJ of energy is released every time 1 mol C12H22O11(aq) and 8 mol KClO3(aq) react to form 12 mol CO2(g), 11 mol H2O(l), and 8 mol KCl(aq). We can also write ΔHr per mole of reactant or product,
[latex]\begin{array}{r l} \Delta H_{\text{r}} &= −5960 \text{ kJ} / \text{mol } \text{C}_{12}\text{H}_{22}\text{O}_{11} \\ &= −5960 \text{ kJ} / 8 \text{ mol } \text{KClO}_3 = -745.0 \text{ kJ}/\text{ mol KClO}_3 \\ &=−5960 \text{ kJ} /12 \text{ mol} \text{ CO}_2 = −496.7 \text{ kJ/mol CO}_2 \\ &=−5960 \text{ kJ}/11 \text{ mol H}_2\text{O} = −541.8 \text{ kJ}/\text{ mol H}_2\text{O} \\ &= −5960 \text{ kJ}/8 \text{ mol KCl} = −745.0 \text{ kJ/mol KCl} \end{array}[/latex]
Example 3
100.0 mL of 1.00 mol L−1 AgNO3(aq) and 100.0 mL of 1.00 mol L−1 NaCl(aq), both at 22.4 °C, are mixed in a coffee-cup calorimeter. If the reaction occurs as
Ag+(aq) + Cl−(aq) [latex]\longrightarrow[/latex] AgCl(s)
and the temperature of the solution rises to 30.2 °C, then what is qrxn per mole of AgCl formed. Assume you can ignore qcoffee cup and the mixed solution has specific heat capacity and density equal to that of pure water (1.00 g mL−1).
SOLUTION
qrxn = ΔrH = −6.53 × 104 J mol−1 AgCl = −65.3 kJ mol−1 AgCl
Having trouble figuring out this problem? Consult the following video:
Video 1 Coffee Cup (Solution) Calorimetry Problem Solving Example (15 min 44 s).
Standard State
Enthalpy changes are typically tabulated for reactions in which both the reactants and products are at the same conditions. A standard state is a commonly accepted set of conditions used as a reference point for the determination of properties under other different conditions. For chemists, the IUPAC standard state refers to materials under a pressure of 1 bar and solutions at 1 M, and does not specify a temperature. Many thermochemical tables list values with a standard state of 1 atm. Because the ΔH of a reaction changes very little with such small changes in pressure (1 bar = 0.987 atm), ΔH values (except for the most precisely measured values) are essentially the same under both sets of standard conditions. We will include a superscripted “o” in the enthalpy change symbol to designate standard state. Since the usual (but not technically standard) temperature is 298.15 K, we will use a subscripted “298” to designate this temperature. Thus, the symbol ([latex]{\Delta}H^{\circ}_{298}[/latex]) is used to indicate an enthalpy change for a process occurring under these conditions. The symbol ΔH without the superscripted “o” is used to indicate an enthalpy change for a reaction occurring under nonstandard conditions, i.e. partial pressures are not at 1 bar and/or concentrations of solutes are not 1 M.
The enthalpy changes for many types of chemical and physical processes are available in the reference literature, including those for combustion reactions, phase transitions, and formation reactions.
Phase Change
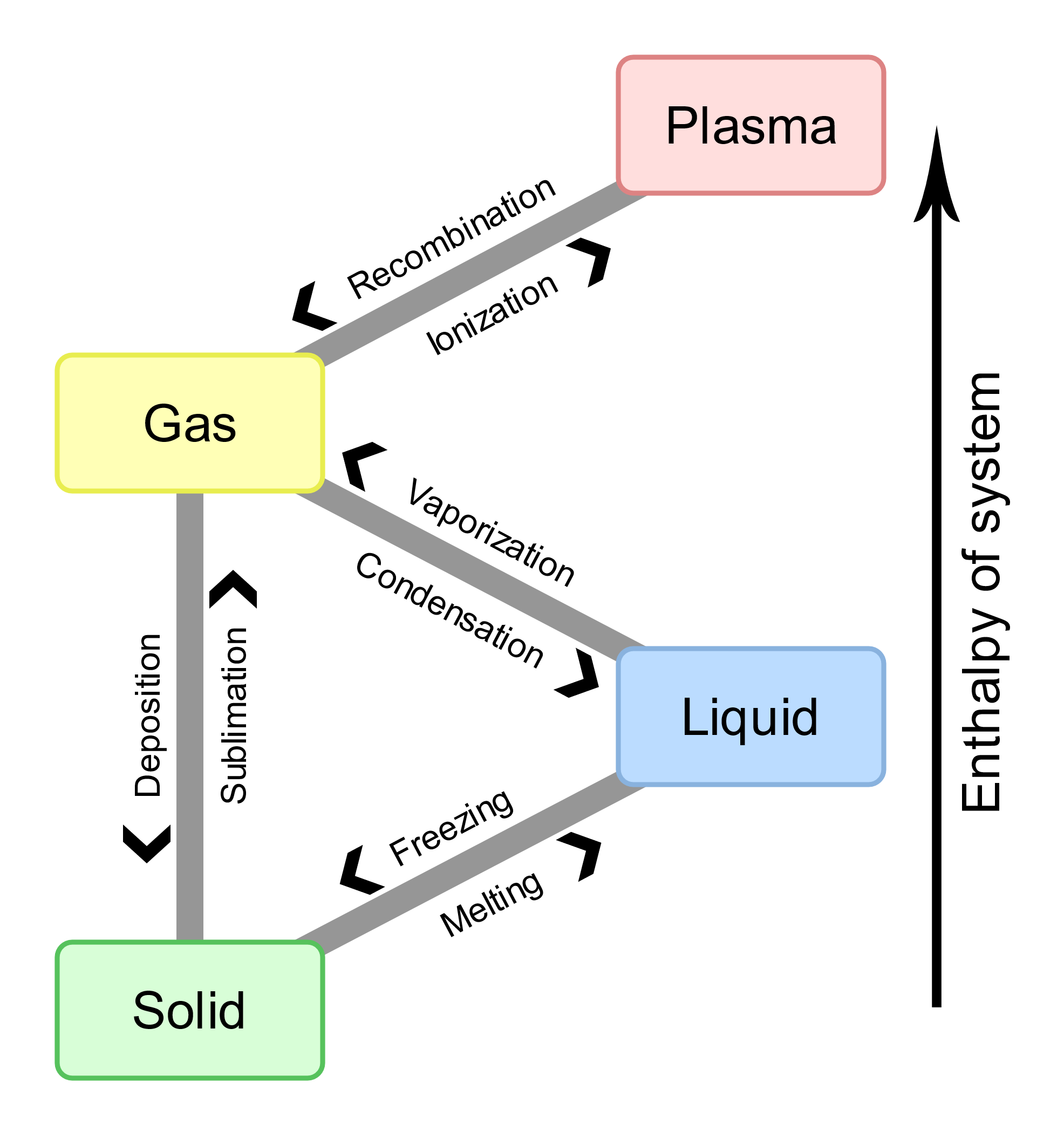
We are all intimately familiar with the reversibility of phase changes. If we put an ice cube tray full of water into the freezer, the water eventually goes from a liquid form to a solid form and we have ice. If we take that ice cube tray full of solid ice out of the freezer and let it sit on the counter, eventually the ice melts back to liquid water. We can then put the tray back in the freezer and freeze the water all over again. It turns out that there is a single temperature (at any given pressure) for a phase transition of a pure substance to be truly reversible, and it is known as the temperature of phase transition. Phase changes are associated with the absorption or release of energy. For a given substance, pressure, and temperature, the gas phase has more energy than the liquid phase, which has more energy than the solid phase. To transition from a solid, to liquid, and to gas phase, energy is absorbed by melting and vaporization. To go in the opposite direction, from a gas, to liquid, to solid phase, energy is released by condensation and freezing. Phase changes are summarized in Figure 1.
So, if we have three common phases of matter, then there must be at least six common phase transitions we can encounter, as we change the phase of a substance between any of solid, liquid, or gas to one of the other two phases. These six phase transitions all have scientific names, but some of them are more well known by more common everyday names. When we go from a solid to a liquid, we often think of this as melting and this will occur at a melting point temperature associated with the given pressure. Scientifically, the term for this phase change from a solid to a liquid is fusion. Of course, we can reverse this phase change from liquid to solid. We often think of this as freezing and could just as easily talk about the freezing point temperature of the substance, and how it is the same as the melting point temperature. Freezing and melting involve the same magnitude of energy, called the enthalpy of fusion (ΔHfus), but in opposite directions. Freezing is exothermic, and melting is endothermic. Using water and ice as an example
[latex]\begin{array}{l l l} &\text{melting (fusion)} \;\;\; &\text{H}_2\text{O}(s) \longrightarrow \text{H}_2\text{O}(l) \;\;\; &\Delta H_{\text{fus}}=+6.01 \text{ kJ/mol} \\ &\text{freezing} \;\;\;& \text{H}_2\text{O}(l) \longrightarrow \text{H}_2\text{O}(s) \;\;\; &\Delta H_{\text{frz}}=-\Delta H_{\text{fus}}=-6.01 \text{ kJ/mol}\end{array}[/latex]
When we go from a liquid to a gas, this is known as vaporization and will be associated with a boiling point temperature at the given pressure of the substance. The energy change is the enthalpy of vaporization (ΔHvap). The opposite change from a gas to a liquid involves the same magnitude of energy as ΔHvap is often referred to as condensation or liquefaction and we can talk about the condensation point temperature. Using water and steam as an example
[latex]\begin{array}{l l l} &\text{vaporization or boiling} \;\;\; &\text{H}_2\text{O}(l) \longrightarrow \text{H}_2\text{O}(g) \;\;\; &\Delta H_{\text{vap}}=+44.01 \text{ kJ/mol} \\ &\text{condensation} \;\;\;& \text{H}_2\text{O}(g) \longrightarrow \text{H}_2\text{O}(l) \;\;\; &\Delta H_{\text{cond}}=-\Delta H_{\text{vap}}=-44.01 \text{ kJ/mol}\end{array}[/latex]
To go from a solid to a gas is known as sublimation while the opposing phase change is referred to as deposition. These would be connected to a sublimation (or deposition point) temperature for a given pressure. The enthalpy of sublimation (ΔHsub) has the same magnitude as the enthalpy of deposition. Using dry ice and gaseous carbon dioxide as an example
[latex]\begin{array}{l l l} &\text{sublimation} \;\;\; &\text{CO}_2(s) \longrightarrow \text{CO}_2 (g) \;\;\; &\Delta H_{\text{sub}}=+26.1 \text{ kJ/mol} \\ &\text{deposition} \;\;\;& \text{CO}_2 (g) \longrightarrow \text{CO}_2(s) \;\;\; &\Delta H_{\text{dep}}=-\Delta H_{\text{sub}}=-26.1 \text{ kJ/mol}\end{array}[/latex]
Enthalpy changes are state functions; hence, the enthalpy of sublimation is approximately the sum of the enthalpy of fusion and the enthalpy of vaporization, ΔHsub = ΔHfus + ΔHvap. In other words, the energy absorbed to transition from solid to gas is approximately equal to the sum of the energy absorbed to transition from solid to liquid and then from liquid to gas. The enthalpy of deposition also has the similar magnitude as ΔHfus + ΔHvap but is exothermic.
Standard Enthalpy of Combustion
Standard enthalpy of combustion ([latex]\Delta H^\circ_{\text{c}}[/latex]) is the enthalpy change when 1 mole of a substance burns (combines vigorously with oxygen) under standard state conditions; it is sometimes called “heat of combustion.” For example, the enthalpy of combustion of ethanol, −1366.8 kJ/mol, is the amount of heat produced when one mole of ethanol undergoes complete combustion at 25 °C and 1 atmosphere pressure, yielding products also at 25 °C and 1 atm.
[latex]\text{C}_2 \text{H}_5 \text{OH}(l) + 3 \text{O}_2(g) \longrightarrow 2 \text{CO}_2 + 3\text{H}_2 \text{O}(l) \;\;\;\;\; \Delta H ^{\circ}_{\text{c, 298}} = -1366.8 \;\text{kJ/mol}[/latex]
Enthalpies of combustion for many substances have been measured; a few of these are listed in Table 1. Many readily available substances with large enthalpies of combustion are used as fuels, including hydrogen, carbon (as coal or charcoal), and hydrocarbons (compounds containing only hydrogen and carbon), such as methane, propane, and the major components of gasoline.
| Substance | Combustion Reaction | Enthalpy of Combustion, [latex]\Delta H^\circ_c (\frac{\text{kJ}}{\text{mol}} \;\text{at 25} \;^\circ \text{C})[/latex] |
|---|---|---|
| carbon | [latex]\text{C}(s) + \text{O}_2(g) \longrightarrow \text{CO}_2(g)[/latex] | −393.5 |
| hydrogen | [latex]\text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{H}_2 \text{O}(l)[/latex] | −285.8 |
| magnesium | [latex]\text{Mg}(s) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{MgO}(s)[/latex] | −601.6 |
| sulfur | [latex]\text{S}(s) + \text{O}_2(g) \longrightarrow \text{SO}_2(g)[/latex] | −296.8 |
| carbon monoxide | [latex]\text{CO}(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{CO}_2(g)[/latex] | −283.0 |
| methane | [latex]\text{CH}_4(g) + 2\text{O}_2(g) \longrightarrow \text{CO}_2(g) + 2\text{H}_2 \text{O}(l)[/latex] | −890.8 |
| acetylene | [latex]\text{C}_2 \text{H}_2(g) + \frac{5}{2} \text{O}_2(g) \longrightarrow 2\text{CO}_2(g) + \text{H}_2 \text{O}(l)[/latex] | −1301.1 |
| ethanol | [latex]\text{C}_2 \text{H}_5 \text{OH}(l) + 3 \text{O}_2(g) \longrightarrow 2\text{CO}_2(g) + 3\text{H}_2 \text{O}(l)[/latex] | −1366.8 |
| methanol | [latex]\text{CH}_3 \text{OH}(l) + \frac{3}{2} \text{O}_2(g) \longrightarrow \text{CO}_2(g) + 2\text{H}_2 \text{O}(l)[/latex] | −726.1 |
| isooctane | [latex]\text{C}_8 \text{H}_{18}(l) + \frac{25}{2} \text{O}_2(g) \longrightarrow 8 \text{CO}_2(g) + 9\text{H}_2 \text{O}(l)[/latex] | −5460 |
| Table 1 Standard Molar Enthalpies of Combustion. Source: OpenStax Chemistry 2e | ||
Example 4
Using Enthalpy of Combustion
The combustion of gasoline is a highly exothermic process. Let us determine the approximate amount of heat produced by burning 1.00 L of gasoline, assuming the enthalpy of combustion of gasoline is the same as that of isooctane, a common component of gasoline. The density of isooctane is 0.692 g/mL.
SOLUTION
Starting with a known amount (1.00 L of isooctane), we can perform conversions between units until we arrive at the desired amount of heat or energy. The enthalpy of combustion of isooctane provides one of the necessary conversions. Table 1 gives this value as −5460 kJ per 1 mole of isooctane (C8H18).
Using these data,
[latex]1.00 \;\rule[0.5ex]{3.75em}{0.1ex}\hspace{-3.75em}\text{L C}_8\text{H}_{18} \times \frac{1000 \;\rule[0.25ex]{3.2em}{0.1ex}\hspace{-3.2em}\text{mL C}_8 \text{H}_{18}}{1 \;\rule[0.25ex]{2.8em}{0.1ex}\hspace{-2.8em}\text{L C}_8 \text{H}_{18}} \times \frac{0.692 \;\rule[0.25ex]{2.65em}{0.1ex}\hspace{-2.65em}\text{g C}_8 \text{H}_{18}}{1 \rule[0.25ex]{3.75em}{0.1ex}\hspace{-3.75em}\;\text{mL C}_8 \text{H}_{18}} \times \frac{1 \;\rule[0.25ex]{3.75em}{0.1ex}\hspace{-3.75em}\text{mol C}_8 \text{H}_{18}}{114 \;\rule[0.25ex]{2.7em}{0.1ex}\hspace{-2.7em}\text{g C}_8 \text{H}_{18}} \times \frac{-5460 \;\text{kJ}}{1 \;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol C}_8 \text{H}_{18}} = \boxed{-3.31 \times 10^4\text{kJ}}[/latex]
The combustion of 1.00 L of isooctane produces 33,100 kJ of heat. (This amount of energy is enough to melt 99.2 kg, or about 218 lbs, of ice.)
Note: If you do this calculation one step at a time, you would find:
[latex]\begin{array}{l} 1.00 \;\text{L C}_8\text{H}_{18} \longrightarrow 1.00 \times 10^3 \;\text{mL C}_8 \text{H}_{18} \\[1em] 1.00 \times 10^3 \;\text{mL C}_8 \text{H}_{18} \longrightarrow 692 \;\text{g C}_8 \text{H}_{18} \\[1em] 692 \;\text{g C}_8 \text{H}_{18} \longrightarrow 6.07 \;\text{mol C}_8 \text{H}_{18} \\[1em] 6.07 \;\text{mol C}_8 \text{H}_{18} \longrightarrow -3.31 \times 10^4 \text{ kJ} \end{array}[/latex]
Standard Enthalpy of Formation
A standard enthalpy of formation [latex]\Delta H^\circ_\text{f}[/latex] is an enthalpy change for a reaction in which exactly 1 mole of a pure substance is formed from free elements in their most stable states under standard state conditions. Some texts use the notation [latex]\Delta _\text{f}H^\circ[/latex]. These values are especially useful for computing or predicting enthalpy changes for chemical reactions that are impractical or dangerous to carry out, or for processes for which it is difficult to make measurements. If we have values for the appropriate standard enthalpies of formation, we can determine the enthalpy change for any reaction.
The standard enthalpy of formation of CO2(g) is −393.5 kJ/mol. This is the enthalpy change for the exothermic reaction
[latex]\text{C}(s) + \text{O}_2(g) \longrightarrow \text{CO}_2(g) \;\;\;\;\; \Delta H^\circ_\text{f, 298} = -393.5 \;\text{kJ/mol}[/latex]
starting with the reactants at a pressure of 1 atm and 25 °C (with the carbon present as graphite, the most stable form of carbon under these conditions) and ending with one mole of CO2, also at 1 atm and 25 °C. For nitrogen dioxide, NO2(g), [latex]\Delta H^\circ_\text{f}[/latex] is +33.2 kJ/mol. This is the enthalpy change for the reaction
[latex]\frac{1}{2} \text{N}_2(g) + \text{O}_2(g) \longrightarrow \text{NO}_2(g) \;\;\;\;\; \Delta H^\circ_\text{f, 298} = +33.2 \;\text{kJ/mol}[/latex]
A reaction equation with [latex]\frac{1}{2}[/latex] mole of N2 and 1 mole of O2 is correct in this case because the standard enthalpy of formation always refers to 1 mole of product, NO2(g).
You will find a table of standard enthalpies of formation of many common substances here (Source: OpenStax Chemistry 2e). These values indicate that formation reactions range from highly exothermic (such as −2984 kJ/mol for the formation of P4O10) to strongly endothermic (such as +226.7 kJ/mol for the formation of acetylene, C2H2). By definition, the standard enthalpy of formation is zero for an element in its most stable form and for H+(aq)
Equation 2
[latex]\Delta H^{\circ}_{\text{f}} = 0 \text{ kJ/mol}[/latex] for an element in the most stable form and for H+(aq)
- [latex]\Delta H^{\circ}_{\text{f}}[/latex], standard enthalpy of formation ([latex]\text{kJ/mol}[/latex])
Example 5
Writing Formation Equations
Write the formation reaction equations for:
(a) C2H5OH(l)
(b) Ca3(PO4)2(s)
SOLUTION
Remembering that formation reaction equations are for forming 1 mole of the compound from its constituent elements under standard conditions, we have:
(a) [latex]2\text{C}(s, \;\text{graphite}) + 3\text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{C}_2 \text{H}_5 \text{OH}(l)[/latex]
(b) [latex]3\text{Ca}(s) + \frac{1}{2} \text{P}_4(s) + 4\text{O}_2(g) \longrightarrow \text{Ca}_3 (\text{PO}_4)_2(s)[/latex]
Note: The standard state of carbon is graphite, and phosphorus exists as P4.
Example 6
Evaluating an Enthalpy of Formation
Ozone, O3(g), forms from oxygen, O2(g), by an endothermic process. Ultraviolet radiation is the source of the energy that drives this reaction in the upper atmosphere. Assuming that both the reactants and products of the reaction are in their standard states, determine the standard enthalpy of formation, [latex]\Delta H^{\circ}_\text{f}[/latex] of ozone from the following information
[latex]3\text{O}_2(g) \longrightarrow 2\text{O}_3(g) \;\;\;\;\; \Delta H^\circ_{298} = +286 \;\text{kJ}[/latex]
SOLUTION
[latex]\Delta H^\circ_\text{f}[/latex] is the enthalpy change for the formation of one mole of a substance in its standard state from the elements in their standard states. Thus, [latex]\Delta H^\circ_\text{f}[/latex] for O3(g) is the enthalpy change for the reaction
[latex]\frac{3}{2} \text{O}_2(g) \longrightarrow \text{O}_3(g)[/latex]
For the formation of 2 mol of O3(g), [latex]\Delta H^\circ_{298} = +286 \;\text{kJ}[/latex]. This ratio, [latex](\frac{286 \;\text{kJ}}{2 \;\text{mol O}_3})[/latex], can be used as a conversion factor to find the heat produced when 1 mole of O3(g) is formed, which is the enthalpy of formation for O3(g)
[latex]\Delta H^\circ \;\text{for 1 mole of O}_3(g) = 1 \;\rule[0.5ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol O}_3 \times \frac{286 \;\text{kJ}}{2 \;\rule[0.25ex]{2.5em}{0.1ex}\hspace{-2.5em}\text{mol O}_3} = 143 \;\text{kJ}[/latex]
Therefore, [latex]\Delta H^\circ_\text{f} [\text{O}_3(g)] = \boxed{+143 \;\text{kJ/mol}}[/latex].
Data Table
Standard enthalpies of formation for select substances (Source: OpenStax Chemistry 2e)
Optional Resources
Watch a video explanation about phase changes. Be familiar with the terminology of phase changes, but the concept of entropy will be addressed in Section 5.5 and onward. Pressure-temperature phase diagrams are beyond the scope of the course.
Video 2 Phase Changes, Heats of Fusion and Vaporization, and Phase Diagrams (4 min 50 s).
Watch a video demonstration of iodine transitioning between solid and vapour phases.
Video 3 Chemistry experiment 47 – Sublimation of Iodine (1 min 39 s).
Optional Activities
Explore a simulation on phase changes. Select the “States” option. Choose among neon, argon, oxygen, and water. Drag the switch on the bucket toward “heat” or “cool” and observe the motion of particles when transitioning between solid, liquid, and gas phases.
Simulate a calorimetry experiment involving heat of solution. Select the “Experiment” tab. In Experiment Step 1, go to the solids tab and choose “Lithium chloride – LiCl”. Select 25.0 g, 20.0 [latex]^\circ[/latex]C, and show [latex]\Delta[/latex]H solution. In Experiment Step 2, use 250 g water at 20.0 [latex]^\circ[/latex]C, and show specific heat. Select “Show graph view” and start the experiment. The final temperature of the solution is 37.63 [latex]^\circ[/latex]C. The solution became warm because the enthalpy of solution is negative, meaning exothermic.
Based on your understanding of state functions, if the molar enthalpy of sublimation of a substance is 87.3 kJ/mol and the molar enthalpy of melting for the same substance is 9.1 kJ/mol, then what would be the molar enthalpy of condensation for the substance?
Click to see answer
The enthalpy for sublimation (solid to gas) is the sum of the enthalpy for fusion (solid to liquid) and for vaporization (liquid to gas),
[latex]\begin{align} \Delta H_{\text{sub}} &= \Delta H_{\text{fus}} + \Delta H_{\text{vap}} \\ \Delta H_{\text{vap}} &= \Delta H_{\text{sub}} - \Delta H_{\text{fus}} \\ &= 87.3 \text{ kJ/mol} – 9.1 \text{ kJ/mol} \\ &= 78.2 \text{ kJ/mol} \end{align}[/latex]
While vaporization is endothermic, condensation is exothermic. The enthalpy of condensation is -78.2 kJ/mol.

