Unit 6 Electrochemistry
6.1 Redox Reactions
OpenStax
Section Learning Objectives
- Define oxidation, reduction, oxidizing agent, and reducing agent.
- Identify redox reactions using oxidation numbers.
- Balance redox reactions in neutral, acidic, and basic solution.
✓ SECTION 6.1 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion. | No | 60 min |
| Optional Resource: Watch video examples of balancing redox equations. | No | 19 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 20 min |
📖 READING PORTION
Oxidation-Reduction Reactions
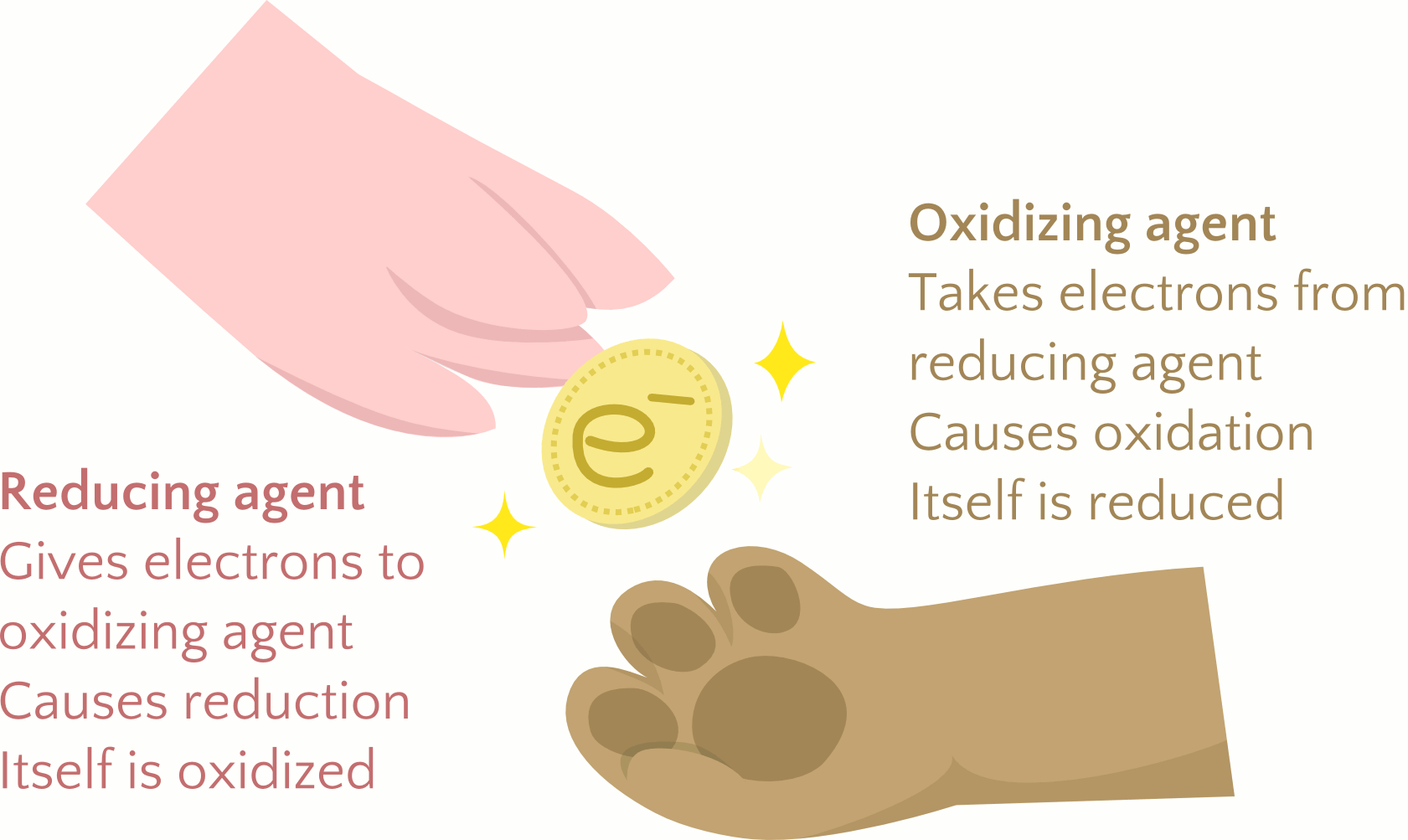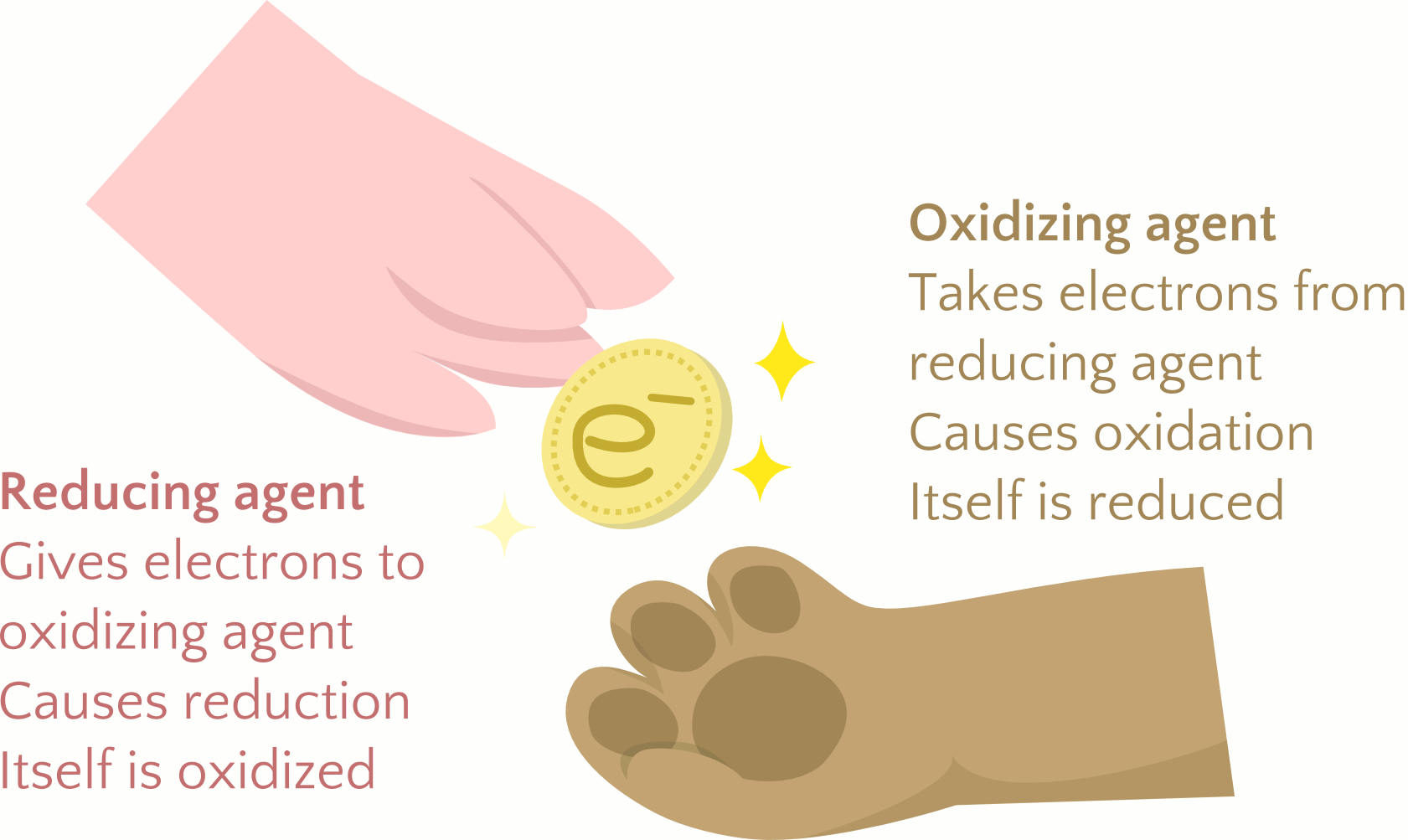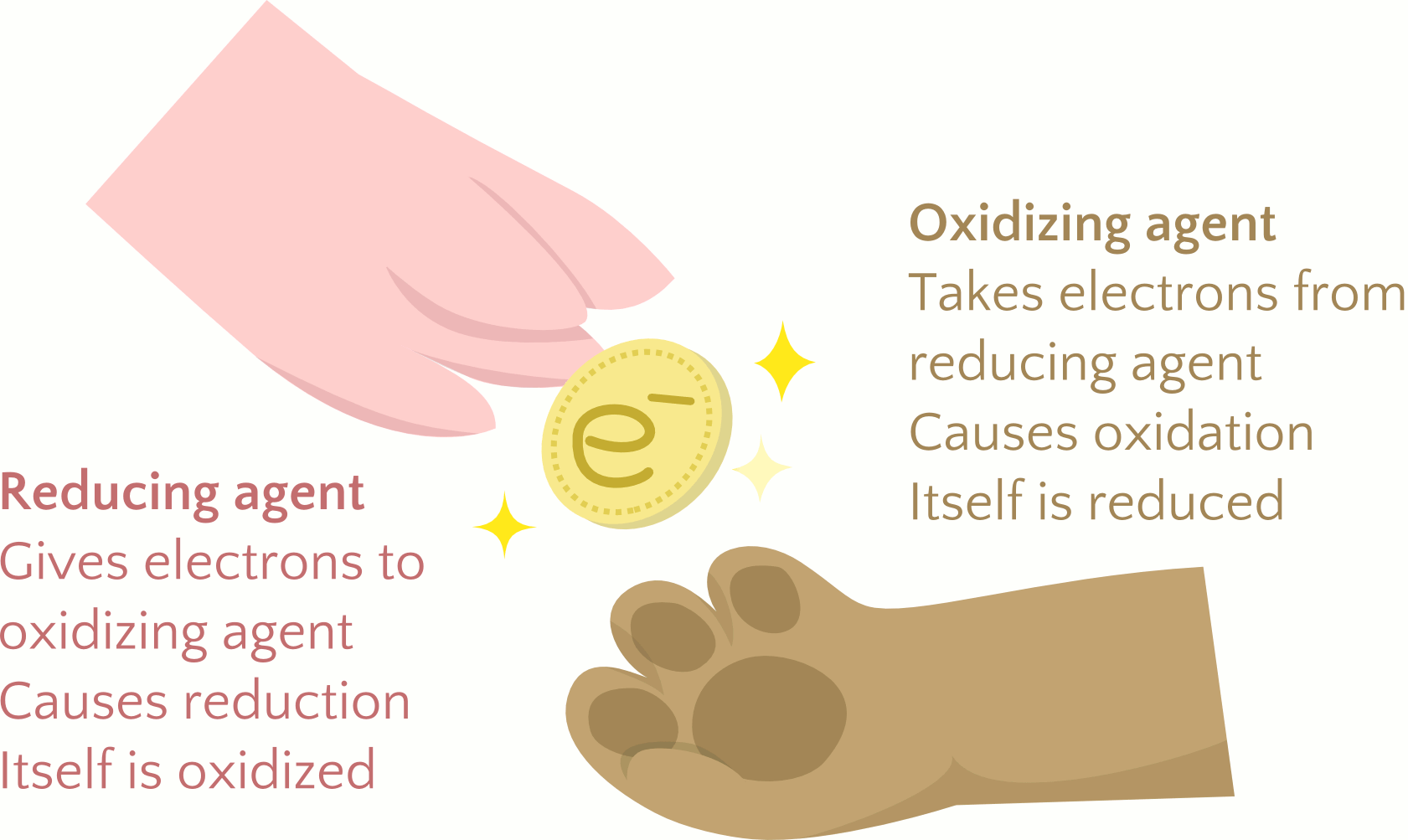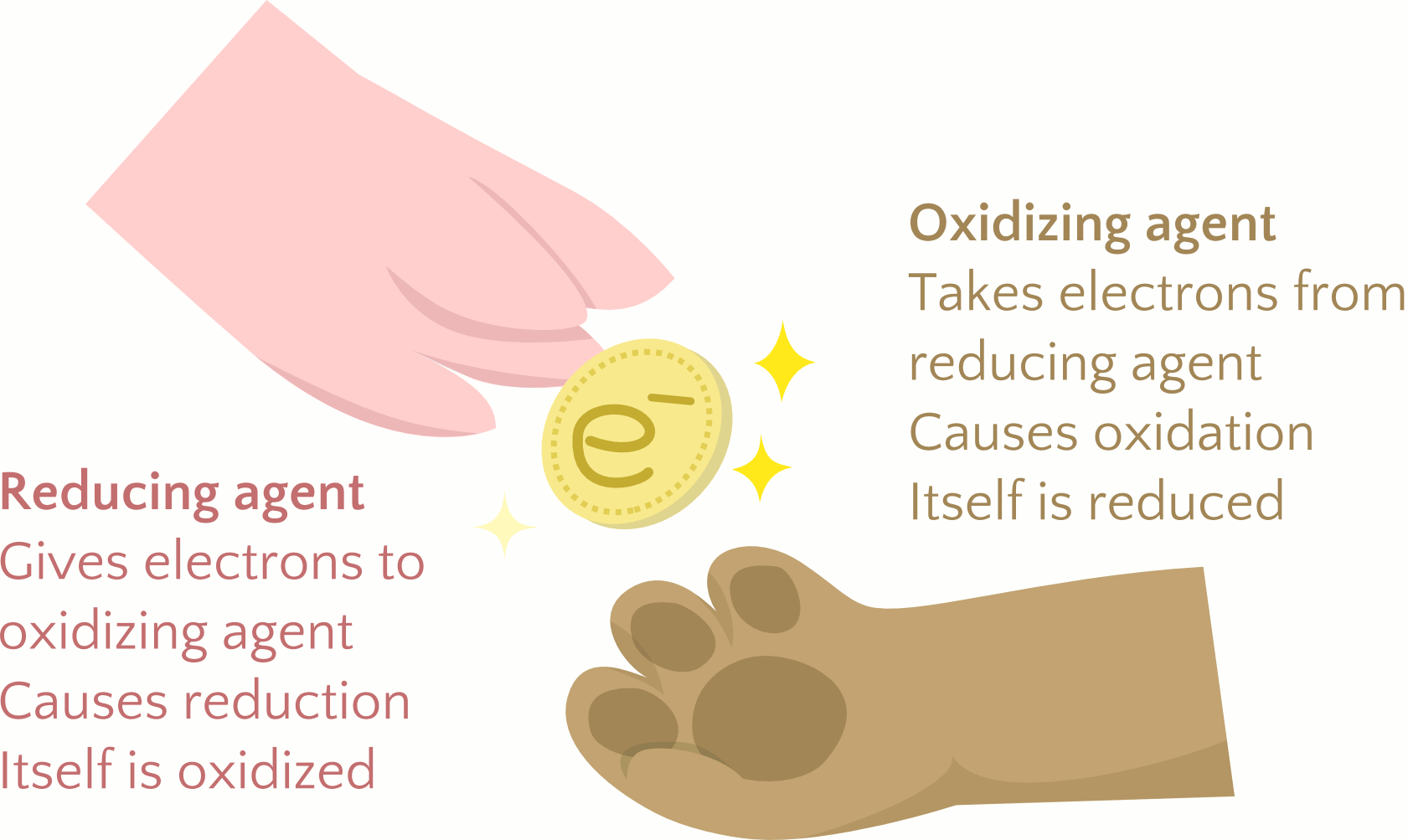
Earth’s atmosphere contains about 20% molecular oxygen, O2, a chemically reactive gas that plays an essential role in the metabolism of aerobic organisms and in many environmental processes that shape the world. The term oxidation was originally used to describe chemical reactions involving O2, but its meaning has evolved to refer to a broad and important reaction class known as oxidation-reduction (redox) reactions.
Redox reactions involve the transfer of electrons between reactant species and are distinct from other reaction types, such as acid-base, which involve the transfer of protons. Oxidation is the loss of electron(s), and reduction is the gain of electron(s). One reactant, called the reducing agent or reductant, gives electron(s) to another reactant, called the oxidizing agent or oxidant. The reducing and oxidizing agents are named such because these species cause the other species to undergo reduction and oxidation, respectively. The reducing agent itself loses electron(s) and undergoes oxidation. The oxidizing agent gains electron(s) and undergoes reduction. The similarity in the terminology can be confusing. It is important to understand the differences between oxidizing and reducing agents, summarized in Figure 1. Because there cannot be a shortage or excess of electrons left over, redox reactions must have both a reducing agent and an oxidizing agent that exchange the same number of electrons. A few examples of redox reactions will be used to develop a clear picture of this classification.
Some redox reactions produce ions, such as the reaction between sodium and chlorine to yield sodium chloride
[latex]2\text{Na}(s) + \text{Cl}_2(g) \longrightarrow 2\text{NaCl}(s)[/latex]
It is helpful to view the process with regard to each individual reactant, that is, to represent the fate of each reactant in the form of an equation called a half-reaction:
[latex]\begin{array}{r l} 2\text{Na}(s) &\longrightarrow 2\text{Na}^{+}(s) + 2\text{e}^{-} \\\text{Cl}_2(g) + 2\text{e}^{-} &\longrightarrow 2\text{Cl}^{-}(s) \end{array}[/latex]
These equations show that Na atoms lose electrons while Cl atoms (in the Cl2 molecule) gain electrons, the “(s)” subscripts for the resulting ions signifying they are present in the form of a solid ionic compound. For redox reactions of this sort, the loss and gain of electrons define the complementary processes that occur.
[latex]\begin{array}{r @ {{}={}} l} \pmb{\text{oxidation}} & \text{loss of electrons} \\[1em] \pmb{\text{reduction}} & \text{gain of electrons} \end{array}[/latex]
In this reaction, then, sodium is oxidized and chlorine is reduced. Viewed from a more active perspective, sodium functions as a reducing agent, by giving electrons to (or reducing) chlorine. Likewise, chlorine functions as an oxidizing agent, by removing electrons from (oxidizing) sodium.
[latex]\begin{array}{r @ {{}={}} l} \pmb{\text{reducing agent}} & \text{species that is oxidized} \\[1em] \pmb{\text{oxidizing agent}} & \text{species that is reduced} \end{array}[/latex]
Some redox processes, however, do not form ions. Consider, for example
[latex]\text{H}_2(g) + \text{Cl}_2(g) \longrightarrow 2 \text{HCl}(g)[/latex]
The product of this reaction is a covalent compound HCl, so transfer of electrons in the explicit sense is not involved. To permit an unambiguous definition of redox reactions, a property called oxidation number has been defined. The oxidation number of an element in a compound is the charge its atoms would possess if the compound was ionic. The following guidelines are used to assign oxidation numbers to each element in a molecule or ion
- The oxidation number of an atom in an elemental substance is zero.
- The oxidation number of a monatomic ion is equal to the ion’s charge.
- Oxidation numbers for common nonmetals are usually assigned as follows:
- Hydrogen: +1 when combined with nonmetals, −1 when combined with metals
- Oxygen: −2 in most compounds, sometimes −1 (so-called peroxides, O22−), very rarely [latex]-\frac{1}{2}[/latex] (so-called superoxides, O2−), positive values when combined with fluorine (values vary)
- Halogens: −1 for fluorine always, −1 for other halogens except when combined with oxygen or other halogens (positive oxidation numbers in these cases, varying values)
- The sum of oxidation numbers for all atoms in a molecule or polyatomic ion equals the charge on the molecule or ion.
The proper convention for reporting charge is to write the number first, followed by the sign (e.g., 2+), while oxidation number is written with the reversed sequence, sign followed by number (e.g., +2). This convention aims to emphasize the distinction between these two related properties.
Example 1
Assigning Oxidation Numbers
Assign oxidation numbers to all the elements in the following species:
(a) H2S
(b) SO32−
(c) Na2SO4
SOLUTION
(a) According to guideline 1, the oxidation number for H is +1. Using this oxidation number and the compound’s formula, guideline 4 may then be used to calculate the oxidation number for sulfur
[latex]\text{charge on H}_2 \text{S} = 0 = (2 \times +1) + (1 \times x)[/latex]
[latex]x = 0 = - (2 \times +1) = -2[/latex]
(b) Guideline 3 suggests the oxidation number for oxygen is −2. Using this oxidation number and the ion’s formula, guideline 4 may then be used to calculate the oxidation number for sulfur
[latex]{\text{charge on SO}_3}^{2-} = -2 = (3 \times -2) + (1 \times x)[/latex]
[latex]x = -2 - (3 \times -2) = +4[/latex]
(c) For ionic compounds, it’s convenient to assign oxidation numbers for the cation and anion separately. According to guideline 2, the oxidation number for sodium is +1. Assuming the usual oxidation number for oxygen (-2 per guideline 3), the oxidation number for sulfur is calculated as directed by guideline 4
[latex]{\text{charge on SO}_4}^{2-} = -2 = (4 \times -2) + (1 \times x)[/latex]
[latex]x = -2 -(4 \times -2) = +6[/latex]
Using the oxidation number concept, an all-inclusive definition of redox reaction has been established. Redox reactions are those in which one or more elements involved undergo a change in oxidation number.
[latex]\pmb{\text{oxidation}} = \text{increase in oxidation number}[/latex]
[latex]\pmb{\text{reduction}} = \text{decrease in oxidation number}[/latex]
In the reaction between sodium and chlorine to yield sodium chloride, sodium is oxidized (its oxidation number increases from 0 in Na to +1 in NaCl) and chlorine is reduced (its oxidation number decreases from 0 in Cl2 to −1 in NaCl). In the reaction between molecular hydrogen and chlorine, hydrogen is oxidized (its oxidation number increases from 0 in H2 to +1 in HCl) and chlorine is reduced (its oxidation number decreases from 0 in Cl2 to −1 in HCl).
Several subclasses of redox reactions are recognized, including combustion reactions in which the reductant (also called a fuel) and oxidant (often, but not necessarily, molecular oxygen) react vigorously and produce significant amounts of heat, and often light, in the form of a flame. Solid rocket-fuel reactions are combustion processes. A typical propellant reaction in which solid aluminum is oxidized by ammonium perchlorate is represented by this equation
[latex]10\text{Al}(s) + 6\text{NH}_4 \text{ClO}_4(s) \longrightarrow 4\text{Al}_2 \text{O}_3(s) + 2\text{AlCl}_3(s) + 12\text{H}_2 \text{O}(g) + 3\text{N}_2(g)[/latex]
Single-displacement (replacement) reactions are redox reactions in which an ion in solution is displaced (or replaced) via the oxidation of a metallic element. One common example of this type of reaction is the acid oxidation of certain metals
[latex]\text{Zn}(s) + 2\text{HCl}(aq) \longrightarrow \text{ZnCl}_2(aq) + \text{H}_2(g)[/latex]
Metallic elements may also be oxidized by solutions of other metal salts; for example
[latex]\text{Cu}(s) + 2 \text{AgNO}_3(aq) \longrightarrow \text{Cu(NO}_3)_2(aq) + 2 \text{Ag}(s)[/latex]
This reaction may be observed by placing copper wire in a solution containing a dissolved silver salt. Silver ions in solution are reduced to elemental silver at the surface of the copper wire, and the resulting Cu2+ ions dissolve in the solution to yield a characteristic blue colour (Figure 2).

Example 2
Describing Redox Reactions
Identify which equations represent redox reactions, providing a name for the reaction if appropriate. For those reactions identified as redox, name the oxidant and reductant.
(a) [latex]\text{ZnCO}_3(s) \longrightarrow \text{ZnO}(s) + \text{CO}_2(g)[/latex]
(b) [latex]2\text{Ga}(l) + 3\text{Br}_2(l) \longrightarrow 2\text{GaBr}_3(s)[/latex]
(c) [latex]2\text{H}_2 \text{O}_2(aq) \longrightarrow 2\text{H}_2 \text{O}(l) + \text{O}_2(g)[/latex]
(d) [latex]\text{BaCl}_2(aq) + \text{K}_2 \text{SO}_4(aq) \longrightarrow \text{BaSO}_4(s) + 2\text{KCl}(aq)[/latex]
(e) [latex]\text{C}_2 \text{H}_4(g) + 3\text{O}_2(g) \longrightarrow 2\text{CO}_2(g) + 2\text{H}_2 \text{O}(l)[/latex]
SOLUTION
Redox reactions are identified per definition if one or more elements undergo a change in oxidation number.
(a) This is not a redox reaction, since oxidation numbers remain unchanged for all elements.
(b) This is a redox reaction. Gallium is oxidized, its oxidation number increasing from 0 in Ga(l) to +3 in GaBr3(s). The reducing agent is Ga(l). Bromine is reduced, its oxidation number decreasing from 0 in Br2(l) to −1 in GaBr3(s). The oxidizing agent is Br2(l).
(c) This is a redox reaction. It is a particularly interesting process, as it involves the same element, oxygen, undergoing both oxidation and reduction (a so-called disproportionation reaction). The oxidation number for oxygen is −1 in peroxides as in hydrogen peroxide. Oxygen is oxidized, its oxidation number increasing from −1 in H2O2(aq) to 0 in O2(g). Oxygen is also reduced, its oxidation number decreasing from −1 in H2O2(aq) to −2 in H2O(l). For disproportionation reactions, the same substance functions as an oxidant and a reductant.
(d) This is not a redox reaction, since oxidation numbers remain unchanged for all elements. The reaction is a precipitation reaction.
(e) This is a redox reaction (combustion). Carbon is oxidized, its oxidation number increasing from −2 in C2H4(g) to +4 in CO2(g). The reducing agent (fuel) is C2H4(g). Oxygen is reduced, its oxidation number decreasing from 0 in O2(g) to −2 in H2O(l). The oxidizing agent is O2(g).
Balancing Redox Reactions via the Half-Reaction Method
Redox reactions that take place in aqueous media often involve water, hydronium ions, and hydroxide ions as reactants or products. Although these species are not oxidized or reduced, they do participate in chemical change in other ways (e.g., by providing the elements required to form oxyanions). Equations representing these reactions are sometimes very difficult to balance by inspection, so systematic approaches have been developed to assist in the process. One very useful approach is to use the method of half-reactions to split oxidation-reduction reactions into their oxidation “half” and reduction “half” to make finding the overall equation easier. The steps for balancing redox reactions are as follows:
- Write the two half-reactions representing the redox process.
- Balance all elements except oxygen and hydrogen.
- Balance oxygen atoms by adding H2O molecules.
- Balance hydrogen atoms by adding H+ ions.
- Balance charge by adding electrons. An equation must represent equal numbers of atoms and net electrical charge on the reactant and product sides.
- If necessary, multiply each half-reaction’s coefficients by the smallest possible integers to yield equal numbers of electrons in each.
- Add the balanced half-reactions together and simplify by removing species that appear on both sides of the equation.
This method is also called balancing redox reactions in acidic solution. A neutral solution may be treated as acidic or basic for balancing redox reactions, though treating as acidic is usually easier.
Example 3
Balancing Redox Reactions in Acidic Solution
Write a balanced equation for the reaction between dichromate ion and iron(II) ion to yield iron(III) ion and chromium(III) ion in acidic solution.
[latex]\text{Cr}_2 {\text{O}_7}^{2-}(aq) + \text{Fe}^{2+}(aq) \longrightarrow \text{Cr}^{3+}(aq) + \text{Fe}^{3+}(aq)[/latex]
SOLUTION
Start by collecting the species into an unbalanced oxidation half-reaction and an unbalanced reduction half-reaction. Each of these half-reactions contain the same element in two different oxidation states. The Fe2+ has lost an electron to become Fe3+; therefore, iron underwent oxidation. The reduction is not as obvious; however, the chromium gained three electrons to change from Cr +6, the oxidation number of Cr in Cr2O72−, to Cr3+
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation (charge unbalanced):} & \text{Fe}^{2+}(aq) &\longrightarrow \text{Fe}^{3+}(aq) \\[0.5em] \text{reduction (unbalanced):} & \text{Cr}_2 {\text{O}_7}^{2-}(aq) &\longrightarrow \text{Cr}^{3+}(aq) \end{array}[/latex]
Balance all elements except oxygen and hydrogen. The iron half-reaction is already balanced, but the chromium half-reaction shows two Cr atoms on the left and one Cr atom on the right. Changing the coefficient on the right side of the equation to 2 achieves balance with regard to Cr atoms.
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation (charge unbalanced):} & \text{Fe}^{2+}(aq) &\longrightarrow \text{Fe}^{3+}(aq) \\[0.5em] \text{reduction (unbalanced):} & \text{Cr}_2 {\text{O}_7}^{2-}(aq) &\longrightarrow 2\text{Cr}^{3+}(aq) \end{array}[/latex]
Next, balance oxygen by adding water (H2O), then balance hydrogen by adding hydrogen ion (H+). This step is not necessary in the iron half-reaction because the half-reaction involves neither oxygen nor hydrogen. The chromium half-reaction shows seven O atoms on the left and none on the right, so seven water molecules are added to the right side. The chromium half-reaction shows 14 H atoms on the right and none on the left, so 14 hydrogen ions are added to the left side.
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation (charge unbalanced):} & \text{Fe}^{2+}(aq) &\longrightarrow \text{Fe}^{3+}(aq) \\[0.5em] \text{reduction (charge unbalanced):} & \text{Cr}_2 {\text{O}_7}^{2-}(aq)+ 14\text{H}^{+}(aq) &\longrightarrow 2\text{Cr}^{3+}(aq)+ 7 \text{H}_2 \text{O}(l) \end{array}[/latex]
Balance charge by adding electrons. The iron half-reaction shows a total charge of +2 on the left side (1 Fe2+ ion) and +3 on the right side (1 Fe3+ ion). Adding one electron to the right side brings that side’s total charge to (+3) + (−1) = +2, and charge balance is achieved. The chromium half-reaction shows a total charge of (1) × (−2) + (14) × (+1) = +12 on the left side (1 Cr2O72− ion and 14 H+ ions). The total charge on the right side is (2) × (+3) = +6 (2 Cr3+ ions). Adding six electrons to the left side will bring that side’s total charge to (+12) + (−6) = +6, and charge balance is achieved.
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation (balanced):} & \text{Fe}^{2+}(aq) &\longrightarrow \text{Fe}^{3+}(aq) + \text{e}^{-} \\[0.5em] \text{reduction (balanced):} & \text{Cr}_2 {\text{O}_7}^{2-}(aq)+ 14\text{H}^{+}(aq)+ 6\text{e}^{-} &\longrightarrow 2\text{Cr}^{3+}(aq)+ 7 \text{H}_2 \text{O}(l) \end{array}[/latex]
We can check both half-reactions for the number of each atom type and the total charge on each side of the equation. The charges include the charges of the ions times the number of ions and the −1 charge on an electron times the number of electrons.
[latex]\text{oxidation}[/latex]
[latex]\text{Fe: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(+2)] = [1\;\times\;(+3)\;+\;1\;\times\;(-1)]\text{? Yes.}[/latex]
[latex]\text{reduction}[/latex]
[latex]\text{Cr: Does}\;(1\;\times\;2) = (2\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;7) = (7\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(14\;\times\;1) = (7\;\times\;2)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(-2)\;+\;14\;\times\;(+1)\;+\;6\;\times\;(-1)] = [2\;\times\;(+3)]\text{? Yes.}[/latex]
If the atoms and charges balance, the half-reaction is balanced. Another way to check our work is to notice that, in oxidation half-reactions, electrons appear as products (on the right). Since iron undergoes oxidation, iron is the reducing agent. In reduction half-reactions, electrons appear as reactants (on the left side). Electrons are gained when Cr2O72−, the oxidizing agent, is reduced to Cr3+.
Multiply the two half-reactions so the number of electrons in one reaction equals the number of electrons in the other reaction. Redox reactions involve the transfer (not creation or destruction) of electrons. The oxidation half-reaction generates one electron, while the reduction half-reaction requires six. The lowest common multiple of one and six is six; therefore, it is necessary to multiply every term in the oxidation half-reaction by six and every term in the reduction half-reaction by one. (In this case, the multiplication of the reduction half-reaction generates no change; however, this will not always be the case.) The multiplication of the two half-reactions by the appropriate factor followed by addition of the two halves gives
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation:} &6\text{Fe}^{2+}(aq) &\longrightarrow 6\text{Fe}^{3+}(aq) + 6\text{e}^{-} \\[0.5em] \text{reduction:} & \text{Cr}_2 {\text{O}_7}^{2-}(aq) + 14\text{H}^{+}(aq) + 6\text{e}^{-} &\longrightarrow 2\text{Cr}^{3+}(aq) + 7 \text{H}_2 \text{O}(l)\\[0.5em] \hline \text{overall:} &6\text{Fe}^{2+}(aq) + \text{Cr}_2 {\text{O}_7}^{2-}(aq) + 14\text{H}^{+}(aq) &\longrightarrow 6\text{Fe}^{3+}(aq) + 2\text{Cr}^{3+}(aq) + 7 \text{H}_2 \text{O}(l) \end{array}[/latex]
The electrons do not appear in the final answer because the oxidation electrons are the same electrons as the reduction electrons and they “cancel.” Carefully check each side of the overall equation to verify everything was combined correctly
[latex]\text{Fe: Does}\;(6\;\times\;1) = (6\;\times\;1)\text{? Yes.} \\[0.5em] \text{Cr: Does}\;(1\;\times\;2) = (2\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;7) = (7\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(14\;\times\;1) = (7\;\times\;2)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[6\;\times\;(+3)\;+\;1\;\times\;(-2)\;+\;14\;\times\;(+1)] = [6\;\times\;(+3)\;+\;2\;\times\;(+3)]\text{? Yes.}[/latex]
Everything checks, so the overall equation in acidic solution is correct.
Example 4
Balancing Redox Reactions in Acidic Solution
Consider the following unbalanced oxidation-reduction reaction in acidic solution
[latex]\text{MnO}_4^{\;\;-}(aq)\;+\;\text{Fe}^{2+}(aq)\;{\longrightarrow}\;\text{Mn}^{2+}(aq)\;+\;\text{Fe}^{3+}(aq)[/latex]
Write a balanced equation for the reaction.
SOLUTION
Start by collecting the species into an unbalanced oxidation half-reaction and an unbalanced reduction half-reaction. Each of these half-reactions contain the same element in two different oxidation states. The Fe2+ has lost an electron to become Fe3+; therefore, iron underwent oxidation. The reduction is not as obvious; however, the manganese gained five electrons to change from Mn +7, the oxidation number of Mn in MnO4−, to Mn2+.
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation (charge unbalanced):} & \text{Fe}^{2+}(aq) &\longrightarrow \text{Fe}^{3+}(aq) \\[0.5em] \text{reduction (unbalanced):} & \text{MnO}_4^{\;\;-}(aq) &\longrightarrow \text{Mn}^{2+}(aq) \end{array}[/latex]
Next, balance oxygen by adding water (H2O), then balance hydrogen by adding hydrogen ion (H+). This step is not necessary in the oxidation half-reaction because the half-reaction involves neither oxygen nor hydrogen. However, in the reduction half-reaction, four moles of H2O is added to the product side to balance the four oxygen atoms in MnO4−. Consequently, the total of eight hydrogen atoms brought on by adding four H2O requires eight H+ in the reactant side.
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation (charge unbalanced):} &\text{Fe}^{2+}(aq) &\longrightarrow \text{Fe}^{3+}(aq) \\[0.5em] \text{reduction (charge unbalanced):} & \text{MnO}_4^{\;\;-}(aq)\;+\;8\text{H}^{+}(aq)\; &\longrightarrow \text{Mn}^{2+}(aq)\;+\;4\text{H}_2\text{O}(l) \end{array}[/latex]
The iron in the oxidation half-reaction is balanced, but the charge is unbalanced since the charges on the reactant and product sides are not equal. It is necessary to use electrons to balance the charge by adding electrons to one side of the equation. Adding a single electron on the right side gives a balanced oxidation half-reaction. As for the reduction half-reaction, the total charge on the left of the reaction arrow is (−1) × (1) + (8) × (+1) = +7, while the total charge on the right side is (1) × (+2) + (4) × (0) = +2. The difference between +7 and +2 is five; therefore, it is necessary to add five electrons to the left side to achieve charge balance.
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation (balanced):} & \text{Fe}^{2+}(aq) &\longrightarrow \text{Fe}^{3+}(aq)\;+\;\text{e}^{-} \\[0.5em] \text{reduction (balanced):} & \text{MnO}_4^{\;\;-}(aq)\;+\;8\text{H}^{+}(aq)\;+\;5\text{e}^{-}\;&\longrightarrow \text{Mn}^{2+}(aq)\;+\;4\text{H}_2\text{O}(l) \end{array}[/latex]
We can check both half-reactions for the number of each atom type and the total charge on each side of the equation. The charges include the charges of the ions times the number of ions and the −1 charge on an electron times the number of electrons.
[latex]\text{oxidation}[/latex]
[latex]\text{Fe: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(+2)] = [1\;\times\;(+3)\;+\;1\;\times\;(-1)]\text{? Yes.}[/latex]
[latex]\text{reduction}[/latex]
[latex]\text{Mn: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;4) = (4\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(8\;\times\;1) = (4\;\times\;2)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(-1)\;+\;8\;\times\;(+1)\;+\;5\;\times\;(-1)] = [1\;\times\;(+2)]\text{? Yes.}[/latex]
If the atoms and charges balance, the half-reaction is balanced. Another way to check our work is to notice that, in oxidation half-reactions, electrons appear as products (on the right). Since iron undergoes oxidation, iron is the reducing agent. In reduction half-reactions, electrons appear as reactants (on the left side). Electrons are gained when MnO4−, the oxidizing agent, is reduced to Mn2+.
Combine the two half-reactions to produce a whole reaction. The key to combining the half-reactions is the electrons. The electrons lost during oxidation must go somewhere. These electrons go to cause reduction. The number of electrons transferred from the oxidation half-reaction to the reduction half-reaction must be equal. There can be no missing or excess electrons. In this example, the oxidation half-reaction generates one electron, while the reduction half-reaction requires five. The lowest common multiple of one and five is five; therefore, it is necessary to multiply every term in the oxidation half-reaction by five and every term in the reduction half-reaction by one. (In this case, the multiplication of the reduction half-reaction generates no change; however, this will not always be the case.) The multiplication of the two half-reactions by the appropriate factor followed by addition of the two halves gives
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation:} & 5\;\times\;\left\{\text{Fe}^{2+}(aq)\right. &\longrightarrow \left.\text{Fe}^{3+}(aq)\;+\;\text{e}^{-}\right\} \\[0.5em] \text{reduction:} & \text{MnO}_4^{\;\;-}(aq)\;+\;8\text{H}^{+}(aq)\;+\;5\text{e}^{-} &\longrightarrow \text{Mn}^{2+}(aq)\;+\;4\text{H}_2\text{O}(l) \\[0.5em] \hline \text{overall:} & 5\text{Fe}^{2+}(aq)\;+\;\text{MnO}_4^{\;\;-}(aq)\;+\;8\text{H}^{+}(aq) &\longrightarrow 5\text{Fe}^{3+}(aq)\;+\;\text{Mn}^{2+}(aq)\;+\;4\text{H}_2\text{O}(l) \end{array}[/latex]
The electrons do not appear in the final answer because the oxidation electrons are the same electrons as the reduction electrons and they “cancel.” Carefully check each side of the overall equation to verify everything was combined correctly
[latex]\text{Fe: Does}\;(5\;\times\;1) = (5\;\times\;1)\text{? Yes.} \\[0.5em] \text{Mn: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;4) = (4\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(8\;\times\;1) = (4\;\times\;2)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[5\;\times\;(+2)\;+\;1\;\times\;(-1)\;+\;8\;\times\;(+1)] = [5\;\times\;(+3)\;+\;1\;\times\;(+2)]\text{? Yes.}[/latex]
Everything checks, so the overall equation in acidic solution is correct. If something does not check, the most common error occurs during the multiplication of the individual half-reactions.
Balancing Redox Reactions in Basic Solution
Unlike in acidic solution, basic solution has lower hydrogen ion concentration and higher hydroxide ion concentration. The simplest way to generate the balanced overall equation in basic solution is to start with the balanced equation in acidic solution, then add enough hydroxide ions to neutralize hydrogen ions in the equation. Hydrogen ion combines with hydroxide ion to produce water.
For reactions occurring in basic media (excess hydroxide ions), carry out these additional steps after steps 1-7 for balancing in acidic solution:
- Add OH− ions to both sides of the equation in numbers equal to the number of H+ ions. On the side of the equation containing both H+ and OH− ions, combine these ions to yield water molecules. Simplify the equation by removing any redundant water molecules.
- Check to see that both the number of atoms and the total charges on the reactant and product sides are balanced.
Example 5
Balancing Oxidation-Reduction Reactions in Basic Solution
Balance the following reaction equation in basic solution
[latex]\text{MnO}_4^{\;\;-}(aq)\;+\;\text{Cr(OH)}_3(s)\;{\longrightarrow}\;\text{MnO}_2(s)\;+\;\text{CrO}_4^{\;\;2-}(aq)[/latex]
SOLUTION
Start by collecting similar species into an unbalanced oxidation half-reaction and an unbalanced reduction half-reaction. The oxidation number of chromium increases from +3 in Cr(OH)3 to +6 in CrO42−. Cr(OH)3 is thus the reducing agent, and is itself oxidized, in the oxidation half-reaction. The oxidation number of manganese decreases from +7 in MnO4− to +4 in MnO2. MnO4− is the oxidizing agent, and is itself reduced, in the reduction half-reaction.
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation (unbalanced):} & \text{Cr(OH)}_3(s) &\longrightarrow \text{CrO}_4^{\;\;2-}(aq) \\[0.5em] \text{reduction (unbalanced):} & \text{MnO}_4^{\;\;-}(aq) &\longrightarrow \text{MnO}_2(s) \end{array}[/latex]
Next, balance oxygen by adding water (H2O), then balance hydrogen by adding hydrogen ion (H+). In the oxidation half-reaction, add one molecule of water to the left side. Then, add five H+ on the right side. In the reduction half-reaction, there are four O atoms, as MnO4−, in the left side and two O atoms, as MnO2, in the right side. Add two oxygen atoms to the right side in the from of two molecules of water. The four hydrogen atoms from adding water is balanced by adding four H+ to the left side.
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation (charge unbalanced):}&\text{Cr(OH)}_3(s)\;+\;\text{H}_2\text{O}(l)\;&{\longrightarrow}\;\text{CrO}_4^{\;\;2-}(aq)\;+\;5\text{H}^{+}(aq) \\ \text{reduction (charge unbalanced):}&\;\text{MnO}_4^{\;\;-}(aq)\;+\;4\text{H}^{+}(aq)\;&{\longrightarrow}\;\text{MnO}_2(s)\;+\;2\text{H}_2\text{O}(l)\end{array}[/latex]
The left side of the oxidation half-reaction has a total charge of zero, and the right side has a total charge of −2 + 5 × (+1) = +3. Add three electrons to the right side. The left side of the reduction half-reaction has a total charge of −1 + 4 × (+1) = +3, and the left side has a total charge of zero. Add three electrons to the left side.
[latex]\begin{array}{lr @{{}\longrightarrow{}} l}\text{oxidation (balanced)}: &\;\text{Cr(OH)}_3(s)\;+\;\text{H}_2\text{O}(l)\; &{\longrightarrow}\;\text{CrO}_4^{\;\;2-}(aq)\;+\;5\text{H}^{+}(aq)\;+\;3\text{e}^{-} \\ \text{reduction (balanced):} &\;\text{MnO}_4^{\;\;-}(aq)\;+\;4\text{H}^{+}(aq)\;+\;3\text{e}^{-}\;&{\longrightarrow}\;\text{MnO}_2(s)\;+\;2\text{H}_2\text{O}(l) \end{array}[/latex]
We can check both half-reactions for the number of each atom type and the total charge on each side of the equation. The charges include the charges of the ions times the number of ions and the −1 charge on an electron times the number of electrons.
[latex]\text{oxidation}[/latex]
[latex]\text{Cr: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;3\;+\;1\;\times\;1) = (4\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(1\;\times\;3\;+\;1\;\times\;2) = (5\;\times\;1)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[0 = [1\;\times\;(-2)\;+\;5\;\times\;(+1)\;+\;3\;\times\;(-1)]\text{? Yes.}[/latex]
[latex]\text{reduction}[/latex]
[latex]\text{Mn: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;4) = (1\;\times\;2\;+\;2\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(4\;\times\;1) = (2\;\times\;2)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(-1)\;+\;4\;\times\;(+1)\;+\;3\;\times\;(-1)] = [0]\text{? Yes.}[/latex]
In this case, both half-reactions involve the same number of electrons; therefore, simply add the two half-reactions together.
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{oxidation:} & \text{Cr(OH)}_3(s)\;+\;\text{H}_2\text{O}(l) &\longrightarrow \text{CrO}_4^{\;\;2-}(aq)\;+\;5\text{H}^{+}(aq)\;+\;3\text{e}^{-} \\[0.5em] \text{reduction:} & \text{MnO}_4^{\;\;-}(aq)\;+\;4\text{H}^{+}(aq)\;+\;3\text{e}^{-} &\longrightarrow \text{MnO}_2(s)\;+\;2\text{H}_2\text{O}(l) \\[0.5em] \hline \text{overall:} &\text{MnO}_4^{\;\;-}(aq)\;+\;4\text{H}^{+}(aq)\;+\;\text{Cr(OH)}_3(s)\;+\;\text{H}_2\text{O}(l)\;&{\longrightarrow}\;\text{CrO}_4^{\;\;2-}(aq)\;+\;\text{MnO}_2(s)\;+\;2\text{H}_2\text{O}(l)\;+\;5\text{H}^{+}(aq) \end{array}[/latex]
Both sides of the equation have H+ and H2O. Cancel four H+ and one H2O from both sides of the equation
[latex]\text{MnO}_4^{\;\;-}(aq)\;+\;\text{Cr(OH)}_3(s)\;{\longrightarrow}\;\text{CrO}_4^{\;\;2-}(aq)\;+\;\text{MnO}_2(s)\;+\;\text{H}_2\text{O}(l)\;+\;\text{H}^{+}(aq)[/latex]
Checking each side of the equation
[latex]\text{Mn: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;4\;+\;1\;\times\;3) = (1\;\times\;4\;+\;1\;\times\;2\;+\;1\;\times\;1)\text{? Yes.} \\[0.5em] \text{Cr: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(1\;\times\;3) = (2\;\times\;1\;+\;1\;\times\;1)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(-1)] = [1\;\times\;(-2)\;+\;1\;\times\;(+1)]\text{? Yes.}[/latex]
This is the balanced equation in acidic solution. For a basic solution, add one hydroxide ion to each side to neutralize H+ and simplify
[latex]\text{MnO}_4^{\;\;-}(aq)\;+\;\text{Cr(OH)}_3(s) \;+\;\text{OH}^{-}(aq) \;{\longrightarrow}\;\text{CrO}_4^{\;\;2-}(aq)\;+\;\text{MnO}_2(s)\;+\;\text{H}_2\text{O}(l)\;+\;\text{H}^{+}(aq)\;+\;\text{OH}^{-}(aq)[/latex]
[latex]\text{MnO}_4^{\;\;-}(aq)\;+\;\text{Cr(OH)}_3(s)\; +\;\text{OH}^{-}(aq) \;{\longrightarrow}\;\text{CrO}_4^{\;\;2-}(aq)\;+\;\text{MnO}_2(s)\;+\;2\text{H}_2\text{O}(l)[/latex]
Checking each side of the equation
[latex]\text{Mn: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;1\;+\;1\;\times\;4\;+\;1\;\times\;3) = (1\;\times\;4\;+\;1\;\times\;2\;+\;2\;\times\;1)\text{? Yes.} \\[0.5em] \text{Cr: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(1\;\times\;1\;+\;1\;\times\;3) = (2\;\times\;2)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(-1)\;+\;1\;\times\;(-1)] = [1\;\times\;(-2)]\text{? Yes.}[/latex]
The balanced equation in basic solution is correct.
Example 6
Balancing Redox Reactions in Basic Solution
Consider the following unbalanced oxidation-reduction reaction
[latex]\text{Cl}^{-}(aq)\;+\;\text{MnO}_4^{\;\;-}(aq)\;{\longrightarrow}\;\text{ClO}_3^{\;\;-}(aq)\;+\;\text{MnO}_2(s)[/latex]
Balance the equation in basic solution.
SOLUTION
First, balancing the equation in acid solution gives
[latex]\text{Cl}^{-}(aq)\;+\;2\text{MnO}_4^{\;\;-}(aq)\;+\;2\text{H}^{+}(aq)\;{\longrightarrow}\;\text{ClO}_3^{\;\;-}(aq)\;+\;2\text{MnO}_2(s)\;+\;\text{H}_2\text{O}(l)[/latex]
In basic solution, it is necessary to add two hydroxide ions to each side of the equation to neutralize the two hydrogen ions on the left, thus forming water
[latex]\begin{array}{r l} \text{Cl}^{-}(aq)\;+\;2\text{MnO}_4^{\;\;-}(aq)\;+\;2\text{H}^{+}(aq)\;+\;2\text{OH}^{-}(aq)\;&{\longrightarrow}\;\text{ClO}_3^{\;\;-}(aq)\;+\;2\text{MnO}_2(s)\;+\;\text{H}_2\text{O}(l)\;+\;2\text{OH}^{-}(aq) \\ \text{Cl}^{-}(aq)\;+\;2\text{MnO}_4^{\;\;-}(aq)\;+\;2\text{H}_2\text{O}(l)\;&{\longrightarrow}\;\text{ClO}_3^{\;\;-}(aq)\;+\;2\text{MnO}_2(s)\;+\;\text{H}_2\text{O}(l)\;+\;2\text{OH}^{-}(aq) \end{array}[/latex]
Note that water appears on both sides of the equation. Cancel one H2O from each side of the reaction arrow.
[latex]\text{Cl}^{-}(aq)\;+\;2\text{MnO}_4^{\;\;-}(aq)\;+\;\text{H}_2\text{O}(l)\;{\longrightarrow}\;\text{ClO}_3^{\;\;-}(aq)\;+\;2\text{MnO}_2(s)\;+\;2\text{OH}^{-}(aq)[/latex]
Check each side of the overall equation to make sure there are no errors
[latex]\text{Cl: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{Mn: Does}\;(2\;\times\;1) = (2\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(2\;\times\;4\;+\;1\;\times\;1) = (3\;\times\;1\;+\;2\;\times\;2\;+\;2\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(1\;\times\;2) = (2\;\times\;1)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(-1)\;+\;2\;\times\;(-1)] = [1\;\times\;(-1)\;+\;2\;\times\;(-1)]\text{? Yes.}[/latex]
Everything checks, so the overall equation in basic solution is correct.
Disproportionation and Comproportionation
While the vast majority of redox reactions involve changes in oxidation number for two or more elements, a few interesting exceptions to this trend do exist. Disproportionation occurs when an element is both reduced and oxidized in a reaction. The oxygen in hydrogen peroxide disproportionates to water and oxygen as
[latex]\text{H}_2\text{O}_2(aq)\longrightarrow\text{H}_2\text{O}(l)+\text{O}_2(g)[/latex]
Oxygen has the oxidation number −1 in the reactant H2O2 but in the products is reduced to −2 in H2O and oxidized to 0 in O2.
The opposite is comproportionation, when an element has multiple different oxidation numbers in the reactants but only one oxidation number in the products. In the reaction
[latex]\text{PbO}_2(s) \;+\;2\text{SO}_4^{2-}(aq) \;+\;4\text{H}^{+}\;+\;\text{Pb}(s)\; {\longrightarrow}\;2\text{PbSO}_4(s)\;+\; 2\text{H}_2\text{O} (l)[/latex]
lead has the oxidation numbers +4 in PbO2 and 0 in Pb in the reactants but only one oxidation number +2 in the product PbSO4.
Example 7
Disproportionation
Balance the disproportionation reaction in basic solution
[latex]\text{Cl}_2(g) \;\longrightarrow\;\text{Cl}^-(aq)\;+\;\text{ClO}^-(aq)[/latex]
SOLUTION
Cl2 is reduced to Cl− and oxidized to ClO−
[latex]\begin{array}{l r l} \text{reduction (charge unbalanced): } & \text{Cl}_2(g) &\longrightarrow\text{Cl}^-(aq) \\ \text{oxidation (unbalanced): } &\text{Cl}_2(g) &\longrightarrow\text{ClO}^-(aq) \end{array}[/latex]
Balance species that contain neither oxygen nor hydrogen. In this case, chlorine
[latex]\begin{array}{l r l} \text{reduction (charge unbalanced): } & \text{Cl}_2(g)&\longrightarrow2\text{Cl}^-(aq) \\ \text{oxidation (unbalanced): } &\text{Cl}_2(g)&\longrightarrow2\text{ClO}^-(aq) \end{array}[/latex]
Balance oxygen by adding H2O and then balance hydrogen by adding H+
[latex]\begin{array}{l r l} \text{reduction (charge unbalanced): } & \text{Cl}_2(g)&\longrightarrow2\text{Cl}^-(aq) \\ \text{oxidation (charge unbalanced): } &\text{Cl}_2(g) \;+\;2\text{H}_2\text{O}(l)&\longrightarrow2\text{ClO}^-(aq) \;+\;4\text{H}^+(aq) \end{array}[/latex]
Balance charge by adding e−. Check that the half-reactions are balanced and add the two half-reactions together
[latex]\begin{array}{l r l} \text{reduction (balanced): } & \text{Cl}_2(g) \;+\;2\text{e}^-&\longrightarrow2\text{Cl}^-(aq) \\ \text{oxidation (balanced): } &\text{Cl}_2(g) \;+\;2\text{H}_2\text{O}(l)&\longrightarrow2\text{ClO}^-(aq) \;+\;4\text{H}^+(aq) \;+\;2\text{e}^- \\ \hline \text{overall: } & 2\text{Cl}_2(g) \;+\;2\text{H}_2\text{O}(l)&\longrightarrow2\text{Cl}^-(aq) \;+\;2\text{ClO}^-(aq) \;+\;4\text{H}^+(aq)\end{array}[/latex]
The reaction is in basic solution; hence, neutralize H+ with an equal amount of OH− to form H2O. Cancel any redundant H2O on either side of the equation. Write the coeffcients in lowest terms.
[latex]\begin{array}{r l} 2\text{Cl}_2(g) \;+\;2\text{H}_2\text{O}(l) \;+\;4\text{OH}^-(aq)&\longrightarrow2\text{Cl}^-(aq) \;+\;2\text{ClO}^-(aq) \;+\;4\text{H}^+(aq) \;+\;4\text{OH}^-(aq) \\ 2\text{Cl}_2(g) \;+\;2\text{H}_2\text{O}(l) \;+\;4\text{OH}^-(aq)&\longrightarrow2\text{Cl}^-(aq) \;+\;2\text{ClO}^-(aq) \;+\;4\text{H}_2\text{O}(l) \\ 2\text{Cl}_2(g) \;+\;4\text{OH}^-(aq)&\longrightarrow2\text{Cl}^-(aq) \;+\;2\text{ClO}^-(aq) \;+\;2\text{H}_2\text{O}(l) \\ \text{Cl}_2(g) \;+\;2\text{OH}^-(aq)&\longrightarrow\text{Cl}^-(aq) \;+\;\text{ClO}^-(aq) \;+\;\text{H}_2\text{O}(l) \end{array}[/latex]
Example 8
Comproportionation
Balance the comproportionation reaction in acidic solution
[latex]\text{Br}^-(aq)\;+\;\text{BrO}_3^-(aq)\;\longrightarrow\;\text{Br}_2(l)[/latex]
SOLUTION
BrO3− is reduced to Br2 and Br− is oxidized to Br2
[latex]\begin{array}{l r l} \text{reduction (unbalanced): } & \text{BrO}_3^-(aq)&\longrightarrow\text{Br}_2 (l) \\ \text{oxidation (unbalanced): } &\text{Br}^-(aq)&\longrightarrow\text{Br}_2 (l) \end{array}[/latex]
Balance species that contain neither oxygen nor hydrogen. In this case, bromine
[latex]\begin{array}{l r l} \text{reduction (unbalanced): } & 2\text{BrO}_3^-(aq)&\longrightarrow\text{Br}_2 (l) \\ \text{oxidation (charge unbalanced): } &2\text{Br}^-(aq)&\longrightarrow\text{Br}_2 (l) \end{array}[/latex]
Balance oxygen by adding H2O and then balance hydrogen by adding H+
[latex]\begin{array}{l r l} \text{reduction (charge unbalanced): } & 2\text{BrO}_3^-(aq)\;+\;12\text{H}^+(aq)&\longrightarrow\text{Br}_2 (l)\;+\;6\text{H}_2\text{O}(l) \\ \text{oxidation (charge unbalanced): } &2\text{Br}^-(aq)&\longrightarrow\text{Br}_2 (l) \end{array}[/latex]
Balance charge by adding e−
[latex]\begin{array}{l r l} \text{reduction (balanced): } & 2\text{BrO}_3^-(aq)\;+\;12\text{H}^+(aq)\;+\;10\text{e}^-&\longrightarrow\text{Br}_2 (l)\;+\;6\text{H}_2\text{O}(l) \\ \text{oxidation (balanced): } &2\text{Br}^-(aq)&\longrightarrow\text{Br}_2 (l)\;+\;2\text{e}^- \end{array}[/latex]
Multiply the oxidation half-reaction by five to match the 10 electrons in the reduction half-reaction and add the two half-reactions together
[latex]\begin{array}{l r l} \text{reduction (charge unbalanced): } & 2\text{BrO}_3^-(aq)\;+\;12\text{H}^+(aq)\;+\;10\text{e}^-&\longrightarrow\text{Br}_2 (l)\;+\;6\text{H}_2\text{O}(l) \\ \text{oxidation (charge unbalanced): } & 5\times\left\{ 2\text{Br}^-(aq)\right. &\longrightarrow \left. \text{Br}_2 (l)\;+\;2\text{e}^-\right\} \\ \hline \text{overall: } & 2\text{BrO}_3^-(aq)\;+\;12\text{H}^+(aq)\;+\;10\text{Br}^-(aq)&\longrightarrow6\text{Br}_2 (l)\;+\;6\text{H}_2\text{O}(l)\end{array}[/latex]
Express the stoichiometric coefficients in lowest terms
[latex]\text{BrO}_3^-(aq)\;+\;6\text{H}^+(aq)\;+\;5\text{Br}^-(aq) \longrightarrow3\text{Br}_2 (l)\;+\;3\text{H}_2\text{O}(l)[/latex]
Optional Resource
Watch video examples of balancing redox equations.
Video 1 Balancing Complex Redox Reactions (18 min 46 s).
Consider the reaction
PCl3(l) + Cl2(g) ⟶ PCl5(s)
Identify the reducing and oxidizing agents.
Click to see answer
The oxidation numbers are [latex]\overset{+3}{\text{P}}\overset{-1}{\text{Cl}_3}[/latex], [latex]\overset{0}{\text{Cl}_2}[/latex], [latex]\overset{+5}{\text{P}}\overset{-1}{\text{Cl}_5}[/latex]. The phosphorus atom in PCl3 increased in oxidation number. The reducing agent is PCl3. The chlorine atom in elemental chlorine decreased in oxidation number. The oxidizing agent is Cl2.

