Unit 6 Electrochemistry
6.3 Galvanic Cells
OpenStax
Section Learning Objectives
- Describe the basic components of galvanic cells.
- Use cell notation to describe galvanic cells.
- Compute standard cell potentials.
✓ SECTION 6.3 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion. | No | 90 min |
| Optional Resource: Watch a video summary of redox reactions and the galvanic cell. | No | 10 min |
| Optional Resource: Watch a demonstration of a copper-zinc galvanic cell. | No | 8 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 100 min |
📖 READING PORTION
Galvanic Cells Harness the Electrical Energy of Redox Reactions
Fuel cells are an emerging technological innovation for hydrogen-powered vehicles. Rather than using fossil fuels to power the vehicle, the fuel is hydrogen. Fossil fuel emissions are pollutants, such as carbon monoxide, carbon dioxide, nitric oxide, and nitrogen dioxide. The waste product of hydrogen fuel cells is simply water. The design of fuel cells requires extensive knowledge of electrochemistry.
Galvanic cells, also known as voltaic cells, are electrochemical cells in which spontaneous oxidation-reduction reactions produce electrical energy. A battery is a galvanic cell. When two half-reactions are separated so that electrical current can flow through an external wire, the electrical energy can be used for electrical work, such as powering a light bulb.
Consider the combination of copper and silver half-cells, Figure 1. The silver and copper half-cells each has an electrode submerged partially a beaker of solution. Silver has a higher reduction potential than copper, and we expect oxidation in the copper half-cell and reduction in the silver half-cell. In the oxidation half-cell, the electrode is called the anode, and the electrolyte is the anolyte. Here, the anode is the copper metal, and the anolyte is the 1 M solution of copper(II) nitrate (Cu(NO3)2). In the reduction half-cell, the electrode is called the cathode, and the electrolyte is the catholyte. The cathode is the silver metal, and the catholyte is the 1 M solution of silver nitrate (AgNO3). The redox reaction is
[latex]\begin{align*} &\text{anode (oxidation):} & \text{Cu}(s) &\longrightarrow \text{Cu}^{2+}(aq)\;+\;2\text{e}^{-} \\[0.5em] &\text{cathode (reduction):} & 2\text{Ag}^{+}(aq)\;+\;2\text{e}^{-} &\longrightarrow 2\text{Ag}(s) \\[0.5em] \hline &\text{overall:} & \text{Cu}(s)\;+\;2\text{Ag}^{+}(aq) &\longrightarrow \text{Cu}^{2+}(aq)\;+\;2\text{Ag}(s) \end{align*}[/latex]
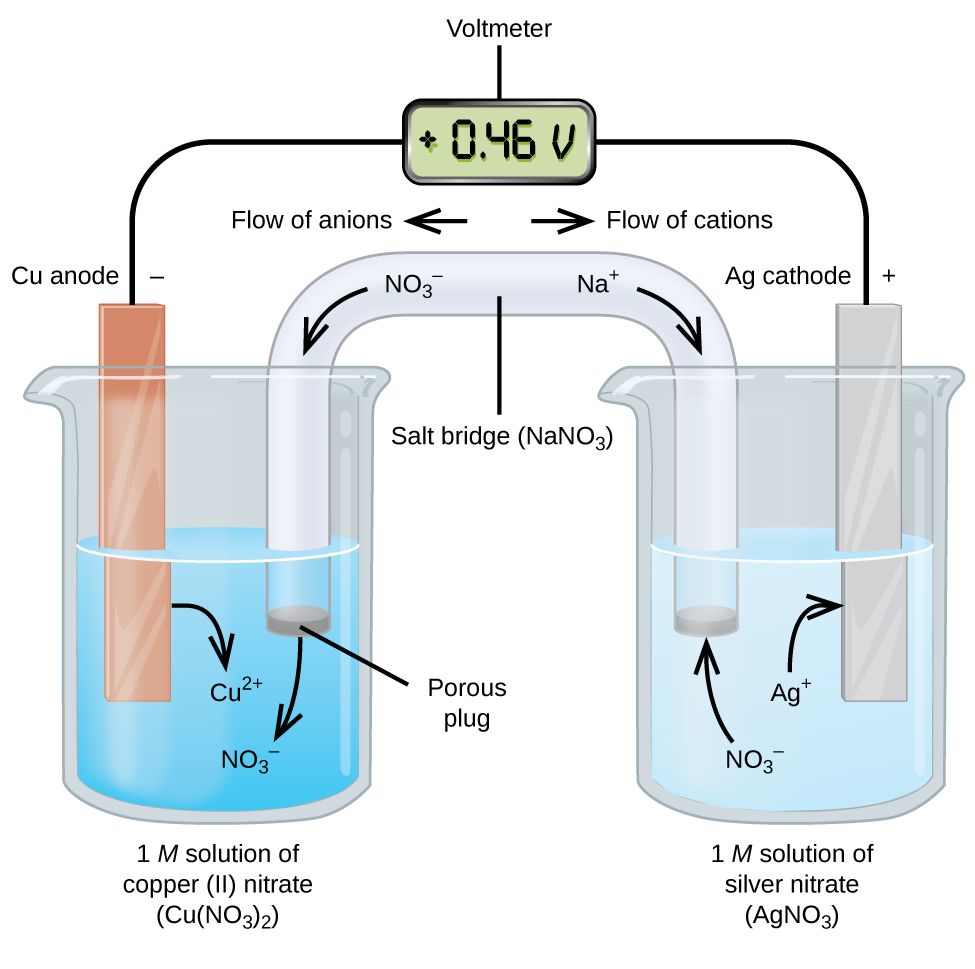
A wire connects the anode to the “−” terminal of a voltmeter and another wire connects the “+” terminal of the voltmeter to the cathode. At this point, no current flows—that is, no significant movement of electrons through the wire occurs because the circuit is open. The circuit is closed using a salt bridge, which allows for electrical balance in the two half-cells. The salt bridge consists of a concentrated, nonreactive, electrolyte solution such as sodium nitrate (NaNO3). Nitrate ions (anions) pass through the porous plug on the left into the copper(II) nitrate solution. This keeps the beaker on the left electrically neutral by neutralizing the charge on the copper(II) ions that are produced in the solution as the copper metal is oxidized. At the same time, sodium ions (cations) move to the right, through the porous plug, and into the silver nitrate solution on the right. These added cations “replace” the silver ions that are removed from the solution as they were reduced to silver metal, keeping the beaker on the right electrically neutral.
The instant the circuit is complete, the voltmeter reads +0.46 V, this is the standard cell potential (E°cell, measured in volts, V). The cell potential can be called the potential difference between the two electrodes or voltage and is created when there is a difference in desire for electrons. Furthermore, the cell potential is a measure of the energy (in joules, J) per unit electrical charge (in coulombs, C) available from the oxidation-reduction reaction.
[latex]\text{volt} = \frac{\text{joule}}{\text{coulomb}}[/latex]
The standard cell potential can also be determined by subtracting the standard reduction potential for the oxidation reaction at the anode from the standard reduction potential for the reduction reaction at the cathode. The minus sign is needed because oxidation is the reverse of reduction.
Equation 1
[latex]E_{\text{cell}}^{\circ} = E_{\text{cathode}}^{\circ}\;-\;E_{\text{anode}}^{\circ}[/latex]
- [latex]E_{\text{cell}}^{\circ}[/latex], standard cell potential (voltage) of the electrochemical cell ([latex]\text{V}[/latex])
- [latex]E^{\circ}[/latex], standard reduction potential of the cathode (reduction half-reaction) or anode (oxidation half-reaction) ([latex]\text{V}[/latex])
An equivalent version of the equation is
[latex]E_{\text{cell}}^{\circ} = E_{\text{reduction}}^{\circ}\;-\;E_{\text{oxidation}}^{\circ}[/latex]
For the copper-silver galvanic cell, we consult Table 1 for the standard reduction potentials. We have
[latex]\begin{eqnarray} E_{\text{cell}}^{\circ} &=& E_{\text{cathode}}^{\circ}\;-\;E_{\text{anode}}^{\circ} \\ &=& E_{\text{Ag}^{+}/\text{Ag}}^{\circ}\;-\;E_{\text{Cu}^{2+}/\text{Cu}}^{\circ} \\ &=& (+0.80\;\text{V})\;-\;(+0.34\;\text{V}) \\ &=& \boxed{+ 0.46\;\text{V}}\end{eqnarray}[/latex]
Multiplying a constant into the stoichiometry of a half-reaction does not affect the reduction potential. Here, the silver half-reaction is doubled, but cathode reduction potential is unchanged. The standard reduction potential represents a potential energy difference much like is experienced for a ball at the top of a hill as compared to the same ball at the bottom of the hill. While the total amount of energy will double if we had two identical balls roll down the hill to the bottom, the hill itself does not double its height just because we decided to roll a second ball down it. So just because two electrons are required to balance the equation does not change the energy difference between an electron found in a silver atom as compared to an electron found in a copper atom.
The cell potential is the voltage derived from a battery. A galvanic cell necessarily has a positive cell potential such that the redox reaction is spontaneous, the oxidizing agent is higher up than the reducing agent on a list of reduction potentials ordered from high to low. If the calculated cell potential is negative, then the redox reaction is nonspontaneous, and the electrochemical cell will not produce electrical energy. We can use Equation 1 to design batteries of a desired voltage by selecting the appropriate reagents from a list of reduction potentials.
Sometimes, a voltmeter may measure a negative cell potential when the voltmeter is connected backwards in the electrical circuit. The backwards connection occurs when the side of the voltmeter that should be attached to the cathode is actually attached to the anode, and vice versa for the other electrode. Such a connection reverses Equation 1 [latex]E_{\text{anode}}^{\circ}\;-\;E_{\text{cathode}}^{\circ}[/latex] to a negative result and means that the reverse redox reaction is spontaneous.
The voltmeter will always measure a voltage (positive if connected the right way, negative if hooked up backwards) and a light bulb will always light up. The only times the light bulb will not light up, or the voltmeter will read zero voltage, are when the redox reaction has reached equilibrium, when the reaction is not a redox reaction (e.g. acid-base, precipitation), or when the salt bridge or wires are not in place.
|
Reduction Half-Reaction |
E° (V) |
| [latex]\text{F}_2(g)\;+\;2\text{e}^{-}\;{\longrightarrow}\;2\text{F}^{-}(aq)[/latex] | +2.866 |
| [latex]\text{PbO}_2(s)\;+\;\text{SO}_4^{\;\;2-}(aq)\;+\;4\text{H}^{+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{PbSO}_4(s)\;+\;2\text{H}_2\text{O}(l)[/latex] | +1.69 |
| [latex]\text{MnO}_4^{\;\;-}(aq)\;+\;8\text{H}^{+}(aq)\;+\;5\text{e}^{-}\;{\longrightarrow}\;\text{Mn}^{2+}(aq)\;+\;4\text{H}_2\text{O}(l)[/latex] | +1.507 |
| [latex]\text{Au}^{3+}(aq)\;+\;3\text{e}^{-}\;{\longrightarrow}\;\text{Au}(s)[/latex] | +1.498 |
| [latex]\text{Cl}_2(g)\;+\;2\text{e}^{-}\;{\longrightarrow}\;2\text{Cl}^{-}(aq)[/latex] | +1.35827 |
| [latex]\text{O}_2(g)\;+\;4\text{H}^{+}(aq)\;+\;4\text{e}^{-}\;{\longrightarrow}\;2\text{H}_2\text{O}(l)[/latex] | +1.229 |
| [latex]\text{Pt}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Pt}(s)[/latex] | +1.20 |
| [latex]\text{Br}_2(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;2\text{Br}^{-}(aq)[/latex] | +1.0873 |
| [latex]\text{Ag}^{+}(aq)\;+\;\text{e}^{-}\;{\longrightarrow}\;\text{Ag}(s)[/latex] | +0.7996 |
| [latex]\text{Hg}_2^{\;\;2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;2\text{Hg}(l)[/latex] | +0.7973 |
| [latex]\text{Fe}^{3+}(aq)\;+\;\text{e}^{-}\;{\longrightarrow}\;\text{Fe}^{2+}(aq)[/latex] | +0.771 |
| [latex]\text{MnO}_4^{\;\;-}(aq)\;+\;2\text{H}_2\text{O}(l)\;+\;3e^{-}\;{\longrightarrow}\;\text{MnO}_2(s)\;+\;4\text{OH}^{-}(aq)[/latex] | +0.558 |
| [latex]\text{I}_2(s)\;+\;2\text{e}^{-}\;{\longrightarrow}\;2\text{I}^{-}(aq)[/latex] | +0.5355 |
| [latex]\text{NiO}_2(s)\;+\;2\text{H}_2\text{O}(l)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Ni(OH)}_2(s)\;+\;2\text{OH}^{-}(aq)[/latex] | +0.49 |
| [latex]\text{Cu}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Cu}(s)[/latex] | +0.337 |
| [latex]\text{Hg}_2\text{Cl}_2(s)\;+\;2\text{e}^{-}\;{\longrightarrow}\;2\text{Hg}(l)\;+\;2\text{Cl}^{-}(aq)[/latex] | +0.26808 |
| [latex]\text{AgCl}(s)\;+\;\text{e}^{-}\;{\longrightarrow}\;\text{Ag}(s)\;+\;\text{Cl}^{-}(aq)[/latex] | +0.22233 |
| [latex]\text{Sn}^{4+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Sn}^{2+}(aq)[/latex] | +0.151 |
| [latex]2\text{H}^{+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{H}_2(g)[/latex] | 0.00 |
| [latex]\text{Pb}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Pb}(s)[/latex] | −0.126 |
| [latex]\text{Sn}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Sn}(s)[/latex] | −0.1262 |
| [latex]\text{Ni}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Ni}(s)[/latex] | −0.257 |
| [latex]\text{Co}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Co}(s)[/latex] | −0.28 |
| [latex]\text{PbSO}_4(s)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Pb}(s)\;+{\;\text{SO}_4}^{2-}(aq)[/latex] | −0.3505 |
| [latex]\text{Cd}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Cd}(s)[/latex] | −0.4030 |
| [latex]\text{Fe}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Fe}(s)[/latex] | −0.447 |
| [latex]\text{Cr}^{3+}(aq)\;+\;3\text{e}^{-}\;{\longrightarrow}\;\text{Cr}(s)[/latex] | −0.744 |
| [latex]\text{Zn}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Zn}(s)[/latex] | −0.7618 |
| [latex]2\text{H}_2\text{O}(l)\;+\;2\text{e}^−\longrightarrow\;\text{H}_2(g)\;+\;2\text{OH}^−(aq)[/latex] | −0.8277 |
| [latex]\text{Mn}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Mn}(s)[/latex] | −1.185 |
| [latex]\text{Zn(OH)}_2(s)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Zn}(s)\;+\;2\text{OH}^{-}(aq)[/latex] | −1.245 |
| [latex]\text{Al}^{3+}(aq)\;+\;3\text{e}^{-}\;{\longrightarrow}\;\text{Al}(s)[/latex] | −1.662 |
| [latex]\text{Mg}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Mg}(s)[/latex] | −2.372 |
| [latex]\text{Na}^{+}(aq)\;+\;\text{e}^{-}\;{\longrightarrow}\;\text{Na}(s)[/latex] | −2.71 |
| [latex]\text{Ca}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Ca}(s)[/latex] | −2.868 |
| [latex]\text{Ba}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Ba}(s)[/latex] | −2.912 |
| [latex]\text{K}^{+}(aq)\;+\;\text{e}^{-}\;{\longrightarrow}\;\text{K}(s)[/latex] | −2.931 |
| [latex]\text{Li}^{+}(aq)\;+\;\text{e}^{-}\;{\longrightarrow}\;\text{Li}(s)[/latex] | −3.04 |
| Table 1 Selected Standard Reduction Potentials at 25 °C. Source: OpenStax Chemistry 2e | |
Example 1
Cell Potentials from Standard Reduction Potentials
What is the standard cell potential for a galvanic cell that consists of Au3+/Au and Ni2+/Ni half-cells? Identify the oxidizing and reducing agents.
SOLUTION
Using Table 1, the reactions involved in the galvanic cell, both written as reductions, are
[latex]\text{Au}^{3+}(aq)\;+\;3\text{e}^{-}\;{\longrightarrow}\;\text{Au}(s)\;\;\;\;\;\;\;E_{\text{Au}^{3+}/\text{Au}}^{\circ} = +1.498\;\text{V}[/latex]
[latex]\text{Ni}^{2+}(aq)\;+\;2\text{e}^{-}\;{\longrightarrow}\;\text{Ni}(s)\;\;\;\;\;\;\;E_{\text{Ni}^{2+}/\text{Ni}}^{\circ} = -0.257\;\text{V}[/latex]
Galvanic cells have positive cell potentials. The reaction at the cathode will be the half-reaction with the more positive standard reduction potential. The reaction at the anode will be the half-reaction with the more negative standard reduction potential. Reversing the reaction at the anode (to show the oxidation) but not its standard reduction potential gives
[latex]\begin{align*} &\text{cathode (reduction):} & \text{Au}^{3+}(aq)\;+\;3\text{e}^{-} &\longrightarrow \text{Au}(s) && E_{\text{cathode}}^{\circ} = E_{\text{Au}^{3+}/\text{Au}}^{\circ} = +1.498\;\text{V} \\[0.5em] &\text{anode (oxidation):} & \text{Ni}(s) &\longrightarrow \text{Ni}^{2+}(aq)\;+\;2\text{e}^{-} && E_{\text{anode}}^{\circ} = E_{\text{Ni}^{2+}/\text{Ni}}^{\circ} = -0.257\;\text{V} \end{align*}[/latex]
To exchange the same number of electrons, the least common factor between the two half-reaction is six. Multiply the reduction half-reaction by two and the oxidation half-reaction by three. The overall reaction is
[latex]3\text{Ni}(s)\;+\;2\text{Au}^{3+}(aq)\;{\longrightarrow}\;3\text{Ni}^{2+}(aq)\;+\;2\text{Au}(s)[/latex]
The reduction potentials are not scaled by the stoichiometric coefficients when calculating the cell potential, and the unmodified standard reduction potentials must be used to calculate E°cell.
[latex]\begin{eqnarray} E_{\text{cell}}^{\circ} &=& E_{\text{cathode}}^{\circ}\;-\;E_{\text{anode}}^{\circ} \\ &=& 1.498\;\text{V}\;-\;(-0.257\;\text{V}) \\ &=& \boxed{+1.755\;\text{V}}\end{eqnarray}[/latex]
From the half-reactions, Ni is oxidized and is the reducing agent. Au3+ is reduced and is the oxidizing agent.
Cell Notation
There are many possible galvanic cells, so a shorthand notation is usually used to describe them. The cell notation (sometimes called a cell diagram) provides information about the various species involved in the reaction. A vertical line, │, denotes a phase boundary and a double line, ‖, the salt bridge. Information about the anode is written to the left, followed by the anode solution, then the salt bridge, then the cathode solution, and, finally, the cathode to the right. Spectator ions are not included. When known, the initial concentrations of the various ions are usually included.
[latex]\text{anode}{\mid}\text{anolyte}{\parallel}\text{catholyte}{\mid}\text{cathode}[/latex]
The cell notation for the galvanic cell in Figure 1 is then
[latex]\text{Cu}(s){\mid}\text{Cu}^{2+}(aq\text{,}\;1\;\text{M}){\parallel}\text{Ag}^{+}(aq\text{,}\;1\;\text{M}){\mid}\text{Ag}(s)[/latex]
If we imagine a wire connecting the anode and cathode, electrons will then travel from the left to the right in the notation. It can be quite daunting at first to memorize a lot of these details but there is an easy trick to remembering them, and it is all based on the orders of the letters in the English alphabet
Anode ⟶ Cathode
Negative ⟶ Positive
Oxidation ⟶ Reduction
Left ⟶ Right
In each case, the first word starts with a letter that comes earlier in the English alphabet than the second word. With this mnemonic you can quickly remember for a galvanic cell diagram or notation that the anode is the negative electrode where oxidation takes place and is always on the left side of the notation while the cathode is the positive electrode where reduction takes place and is always on the right side of the notation.
Example 2
Using Cell Notation
Consider a voltaic cell consisting of
[latex]2\text{Cr}(s)\;+\;3\text{Cu}^{2+}(aq)\;{\longrightarrow}\;2\text{Cr}^{3+}(aq)\;+\;3\text{Cu}(s)[/latex]
Write the oxidation and reduction half-reactions and write the reaction using cell notation. Which reaction occurs at the anode? The cathode?
SOLUTION
By inspecting oxidation numbers, Cr is oxidized when three electrons are lost to form Cr3+, and Cu2+ is reduced as it gains two electrons to form Cu. Oxidation occurs at the anode and reduction at the cathode. Balancing the charge gives
[latex]\begin{align*} &\text{anode (oxidation):} & 2\text{Cr}(s) &\longrightarrow 2\text{Cr}^{3+}(aq)\;+\;6\text{e}^{-} \\[0.5em] &\text{cathode (reduction):} & 3\text{Cu}^{2+}(aq)\;+\;6\text{e}^{-} &\longrightarrow 3\text{Cu}(s) \\[0.5em] \hline \\ &\text{overall:} & 2\text{Cr}(s)\;+\;3\text{Cu}^{2+}(aq) &\longrightarrow 2\text{Cr}^{3+}(aq)\;+\;3\text{Cu}(s) \end{align*}[/latex]
Cell notation uses the simplest form of each of the equations, and starts with the reaction at the anode. No concentrations were specified in the question, so
[latex]\text{Cr}(s){\mid}\text{Cr}^{3+}(aq){\parallel}\text{Cu}^{2+}(aq){\mid}\text{Cu}(s)[/latex]
Example 3
Using Cell Notation
Consider a galvanic cell consisting of
[latex]5\text{Fe}^{2+}(aq)\;+\;\text{MnO}_4^{\;\;-}(aq)\;+\;8\text{H}^{+}(aq)\;{\longrightarrow}\;5\text{Fe}^{3+}(aq)\;+\;\text{Mn}^{2+}(aq)\;+\;4\text{H}_2\text{O}(l)[/latex]
Write the oxidation and reduction half-reactions and write the reaction using cell notation. Which reaction occurs at the anode? The cathode?
SOLUTION
By inspecting oxidation numbers, Fe2+ undergoes oxidation when one electron is lost to form Fe3+, and MnO4− is reduced as Mn +7 gains five electrons to form Mn2+. Oxidation occurs at the anode and reduction at the cathode. Balancing the charge gives
[latex]\begin{array}{lr @{{}\longrightarrow{}} l} \text{anode (oxidation):} & 5\times\{\text{Fe}^{2+}(aq) &\longrightarrow \text{Fe}^{3+}(aq)\;+\;\text{e}^{-}\} \\[0.5em] \text{cathode (reduction):} & \text{MnO}_4^{\;\;-}(aq)\;+\;8\text{H}^{+}(aq)\;+\;5\text{e}^{-} &\longrightarrow \text{Mn}^{2+}(aq)\;+\;4\text{H}_2\text{O}(l) \\[0.5em] \hline \text{overall:} & 5\text{Fe}^{2+}(aq)\;+\;\text{MnO}_4^{\;\;-}(aq)\;+\;8\text{H}^{+}(aq) &\longrightarrow 5\text{Fe}^{3+}(aq)\;+\;\text{Mn}^{2+}(aq)\;+\;4\text{H}_2\text{O}(l) \end{array}[/latex]
It is necessary to use an inert electrode, such as platinum, because there is no metal present to conduct the electrons from the anode to the cathode. No concentrations were specified in the question so
[latex]\text{Pt}(s){\mid}\text{Fe}^{2+}(aq)\text{,}\;\text{Fe}^{3+}(aq){\parallel}\text{MnO}_4^{\;\;-}(aq)\text{,}\;\text{H}^{+}(aq)\text{,}\;\text{Mn}^{2+}(aq){\mid}\text{Pt}(s)[/latex]
Example 4
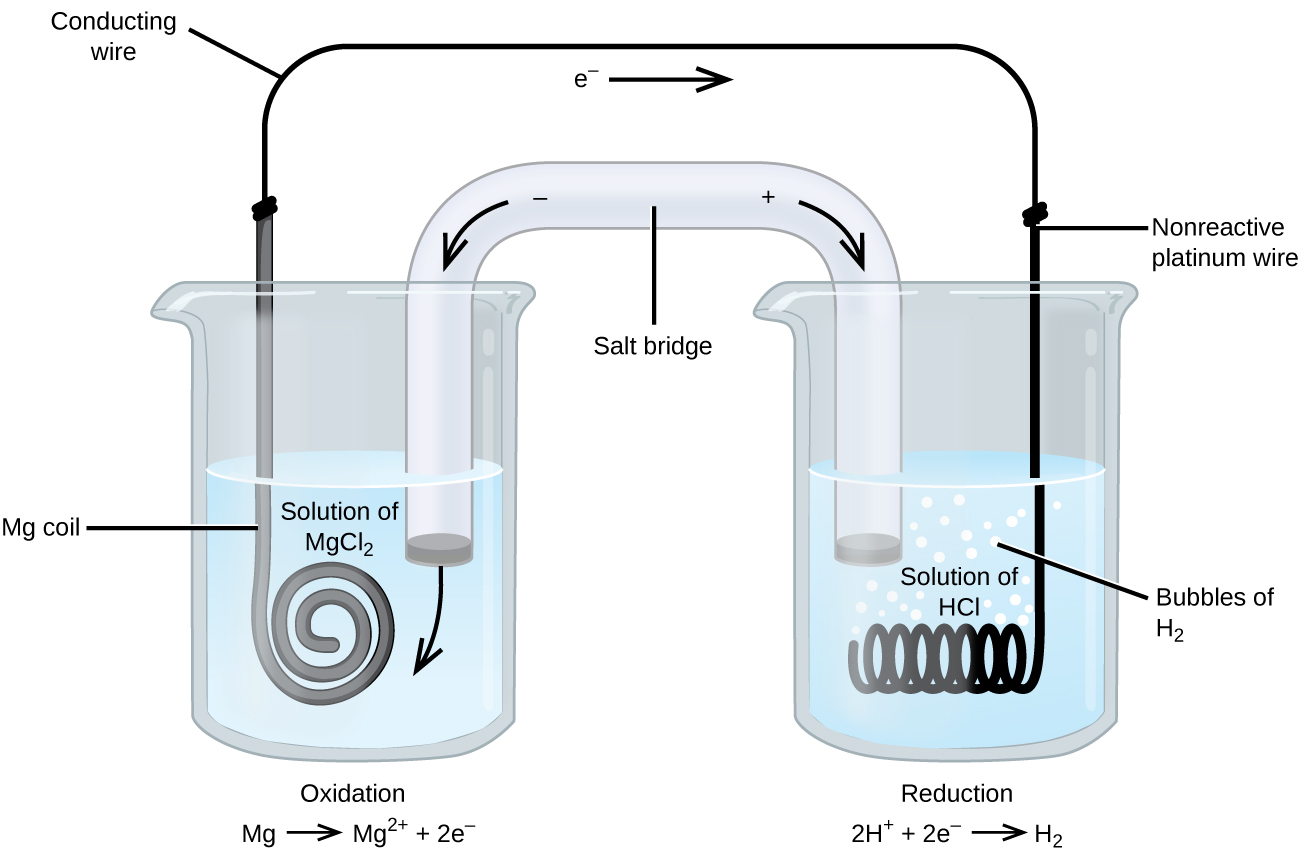
A standard hydrogen half-cell and a standard magnesium half-cell are connected by a conducting wire between the Mg(s) electrode of the magnesium half-cell and the platinum electrode of the hydrogen half-cell. A salt bridge connects the 1 M MgCl(aq) and 1 M HCl(aq) electrolyte solutions. Write the net reaction and the cell notation. What is the standard cell potential?
SOLUTION
According to Table 1, H+ has a higher reduction potential than Mg2+. Magnesium undergoes oxidation at the anode on the left in Figure 2 and hydrogen ions undergo reduction at the cathode on the right. The reaction may be summarized as
[latex]\begin{align*} &\text{anode (oxidation):} & \text{Mg}(s) &\longrightarrow \text{Mg}^{2+}(aq)\;+\;2\text{e}^{-} \\[0.5em] &\text{cathode (reduction):} & 2\text{H}^{+}(aq)\;+\;2\text{e}^{-} &\longrightarrow \text{H}_2(g) \\[0.5em] \hline \\&\text{overall:} & \text{Mg}(s)\;+\;2\text{H}^{+}(aq) &\longrightarrow \text{Mg}^{2+}(aq)\;+\;\text{H}_2(g) \end{align*}[/latex]
The cell uses an inert platinum wire for the cathode, so the cell notation is
[latex]\text{Mg}(s){\mid}\text{Mg}^{2+}(aq\text{, }1\text{ M}){\parallel}\text{H}^{+}(aq\text{, }1\text{ M}){\mid}\text{H}_2(g\text{, }1\text{ atm}){\mid}\text{Pt}(s)[/latex]
Using Equation 1 and Table 1 for the standard reduction potentials. We have
[latex]\begin{eqnarray} E_{\text{cell}}^{\circ} &=& E_{\text{cathode}}^{\circ}\;-\;E_{\text{anode}}^{\circ} \\ &=& E_{\text{H}^{+}/\text{H}_2}^{\circ}\;-\;E_{\text{Mg}^{2+}/\text{Mg}}^{\circ} \\ &=& (0\;\text{V})\;-\;(−2.372\;\text{V}) \\ &=& \boxed{+ 2.372\;\text{V}}\end{eqnarray}[/latex]
Electrolytic Cells
When E or E° is a negative value, the reaction as written is nonspontaneous. The reaction can happen if we supply enough voltage from a battery or direct current power supply. For example, if E = −1.2 V then the reaction can take place if we supply at least 1.2 V. In practice, a bit more voltage is needed, called an overpotential.
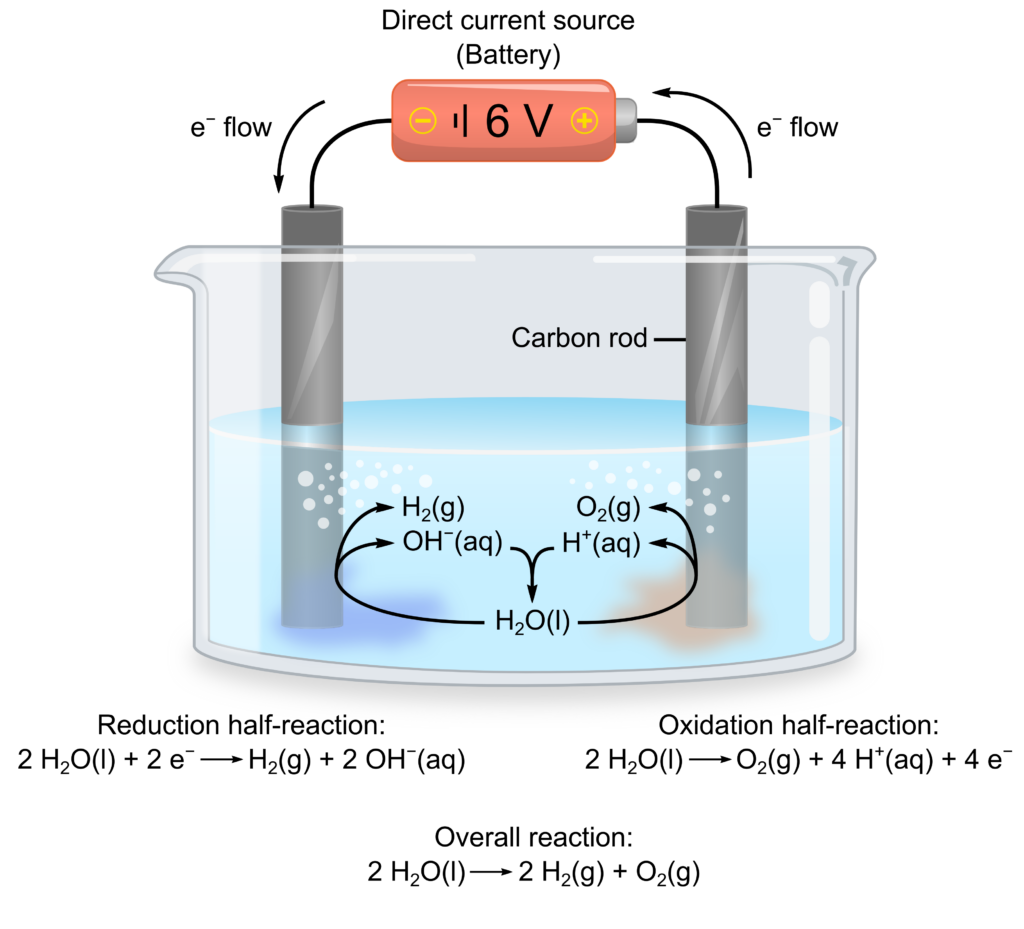
Electrolytic cells have all the reactants in one container instead of two separate half-cells. Therefore, we need to be careful to avoid unwanted reactions, such as corrosion of metal electrodes. In general, the reaction with the least negative E will be favoured. Therefore, water (Figure 3), as well as H+ in acidic conditions or OH− in basic conditions, are possible oxidizing or reducing agents.
Data Table
Standard reduction potentials for select substances (Source: OpenStax Chemistry 2e). The table is listed in alphabetical order of the chemical symbol and not in order of the reduction potentials.
Optional Resources
♦ Watch a video summary of redox reactions and the galvanic cell.
Video 1 Electrochemistry: Crash Course Chemistry #36 (9 min 3 s).
♦ Watch a demonstration of a copper-zinc galvanic cell.
Video 2 Copper-Zinc Voltaic Cell (7 min 11 s).
In a galvanic (voltaic) cell, the half-reaction
MnO4– (aq) + 8 H+(aq) + 5 e– ⟶ Mn2+(aq) + H2O(l)
A) is an oxidation half-reaction that occurs at the anode.
B) is an oxidation half-reaction that occurs at the cathode.
C) is a reduction half-reaction that occurs at the anode.
D) is a reduction half-reaction that occurs at the cathode.
Click to see answer
D) is a reduction half-reaction that occurs at the cathode.

