Unit 6 Electrochemistry
6.4 Relating Cell Potential to Free Energy
OpenStax
Section Learning Objectives
- Relate cell potentials to free energy changes.
- Use the Nernst equation to determine cell potentials at nonstandard conditions.
- Perform calculations that involve converting between cell potentials, free energy changes, and equilibrium constants.
✓ SECTION 6.4 CHECKLIST
| Learning Activity | Graded? | Estimated Time |
|---|---|---|
| Make notes about this section’s reading portion. | No | 90 min |
| Optional Resource: Watch a video example of using the Nernst equation. | No | 6 min |
| Work on the self-check question. | No | 10 min |
| Work on practice exercises. | No | 60 min |
| Complete Unit 6 Assignment on Moodle. | Yes | 200 min |
📖 READING PORTION
Gibbs Free Energy and Voltage
Electricity refers to a number of phenomena associated with the presence and flow of electric charge. Electricity includes such diverse things as lightning, static electricity, the current generated by a battery as it discharges, and many other influences on our daily lives. The flow or movement of charge is an electric current. Electrons or ions may carry the electric charge. The elementary unit of charge is the charge of a proton, which is equal in magnitude to the charge of an electron. The SI unit of charge is the coulomb (C) and the charge of a proton is 1.602 × 10−19 C. The flow of charge is generated by an electrical potential difference, known as potential or voltage, between two points in the circuit. The potential difference between the anode and cathode of a galvanic cell is the cell potential E°cell. The SI unit of electrical potential is the volt (V) and 1 volt = 1 joule/coulomb. When 1 coulomb of charge moves through a potential difference of 1 volt, it gains or loses 1 joule of energy. We will now extend electrochemistry by determining the relationship between E°cell and the thermodynamics quantities ΔG° (Gibbs free energy) and K (equilibrium constant).
In galvanic cells, chemical energy is converted into electrical energy, which can do work. The measured cell potential is the maximum potential the cell can produce and is related to the electrical work (welec) as the product of the charge transferred multiplied by the potential difference (voltage), where the charge in coulombs on 1 mole of electrons is given by Faraday’s constant [latex]F[/latex]
[latex]F = \frac{6.022\;\times\;10^{23}\text{e}^{-}}{\text{mol}}\;\times\;\frac{1.602\;\times\;10^{-19}\;\text{C}}{\text{e}^{-}} = 96485\;\frac{\text{C}}{\text{mol}} = 96485\;\frac{\text{J}}{\text{mol}{\cdot}\text{V}}[/latex]
The electrical work is thus
Equation 1
[latex]E_\text{cell} = \frac{-w_{\text{elec}}}{nF}\;\;\;\;\;\;\;\text{or}\;\;\;\;\;\;\;w_{\text{elec}} = -nFE_{\text{cell}}[/latex]
- [latex]E_\text{cell}[/latex], cell potential ([latex]\text{V}[/latex])
- [latex]w_{\text{elec}}[/latex], electrical work ([latex]\text{J}[/latex])
- [latex]n[/latex], moles of electrons transferred in the balanced equation
- [latex]F[/latex], Faraday’s constant ([latex]96485\;\frac{\text{J}}{\text{mol}{\cdot}\text{V}}[/latex])
The cell potential can also have units of [latex]\text{J/C}[/latex], equivalent to volt, and Faraday’s constant is [latex]96485\;\frac{\text{C}}{\text{mol}}[/latex].
In this equation, n is the number of moles of electrons for the balanced oxidation-reduction reaction. The negative sign for the work indicates that the electrical work is done by the system (the galvanic cell) on the surroundings. From Section 5.6, Gibbs free energy was defined as the energy that is available to do work. In particular, the change in Gibbs free energy was defined in terms of the maximum work ([latex]\Delta G = w_{\text{max}}[/latex]), which, for electrochemical systems, is [latex]w_{\text{elec}} = -nFE_{\text{cell}}[/latex]
Equation 2
[latex]{\Delta} G=-nFE_{\text{cell}}[/latex]
- [latex]\Delta G[/latex], change in Gibbs free energy ([latex]\text{J}[/latex])
- [latex]n[/latex], moles of electrons transferred in the balanced equation
- [latex]F[/latex], Faraday’s constant ([latex]96485\;\frac{\text{J}}{\text{mol}{\cdot}\text{V}}[/latex])
- [latex]E_{\text{cell}}[/latex], cell potential ([latex]\text{V}[/latex])
and
[latex]{\Delta}G^{\circ} = -nFE_{\text{cell}}^{\circ}[/latex] (at standard state)
The cell potential can also have units of [latex]\text{J/C}[/latex], equivalent to volt, and Faraday’s constant is [latex]96485\;\frac{\text{C}}{\text{mol}}[/latex].
Alternatively, if [latex]n[/latex] is unitless, then [latex]\Delta G[/latex] is the molar change in Gibbs free energy ([latex]\Delta G_{\text{r}}[/latex]) in [latex]\text{J/mol}[/latex].
We can verify the signs are correct when we realize that n and F are positive constants and that galvanic cells, which have positive cell potentials, involve spontaneous reactions. Thus, spontaneous reactions, which have ΔG < 0, must have Ecell > 0.
We can relate standard cell potentials to equilibrium constants, since [latex]{\Delta}G_{\text{r}}^{\circ} = -RT\;\text{ln}\;K[/latex]
[latex]-nFE_{\text{cell}}^{\circ} = -RT\;\text{ln}\;K[/latex]
or
Equation 3
[latex]E_{\text{cell}}^{\circ} = \frac{RT}{nF}\;\text{ln}\;K[/latex]
- [latex]E_{\text{cell}}^{\circ}[/latex], standard cell potential ([latex]\text{V}[/latex])
- [latex]R[/latex], gas constant ([latex]8.314\;\frac{\text{J}}{\text{mol}{\cdot}\text{K}}[/latex])
- [latex]T[/latex], kelvin or absolute temperature
- [latex]n[/latex], number of electrons transferred in the balanced equation (unitless)
- [latex]F[/latex], Faraday’s constant ([latex]96485\;\frac{\text{J}}{\text{mol}{\cdot}\text{V}}[/latex])
- [latex]K[/latex], equilibrium constant
Most of the time, the electrochemical reactions are run at the temperature 298.15 K. This is also the temperature for which we have enthalpy and Gibbs free energy of formation as well as absolute entropy data. Collecting terms at this temperature yields
[latex]\begin{eqnarray} E_{\text{cell}}^{\circ} &=& \frac{RT}{nF}\;\text{ln}\;K \\[1em] &=& \frac{\left(8.314\frac{\text{J}}{\text{mol}{\cdot}\text{K}}\right)(298.15 \text{ K})}{n\; \left(\;96485\;\frac{\text{J}}{\text{mol}{\cdot}\text{V}}\right) }\;\text{ln}\;K \\[1em] &=& \frac{0.0257\;\text{V}}{n}\;\text{ln}\;K \end{eqnarray}[/latex]
where n is the number of moles of electrons. For historical reasons, the logarithm in equations involving cell potentials is often expressed using base 10 logarithms (log), which changes the constant by a factor of 2.303
Equation 4
[latex]E_{\text{cell}}^{\circ} = \frac{0.0592\;\text{V}}{n}\;\text{log}\;K[/latex] (at 298.15 K)
- [latex]E_{\text{cell}}^{\circ}[/latex], standard cell potential ([latex]\text{V}[/latex])
- [latex]n[/latex], number of electrons transferred in the balanced equation (unitless)
- [latex]K[/latex], equilibrium constant
![]()
If the temperature is not 298.15 K, it is necessary to use Equation 3 and input the appropriate temperature.
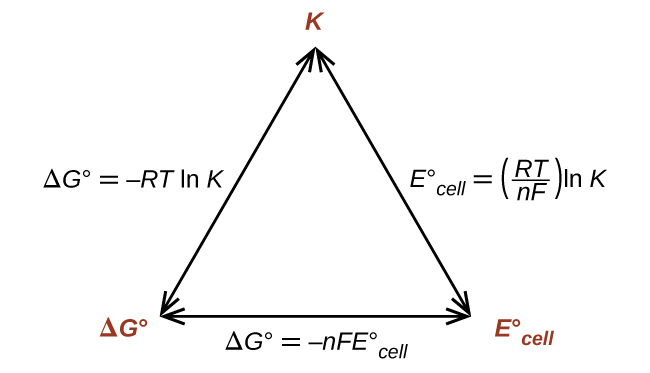
Thus, if ΔG°, K, or E°cell is known or can be calculated, the other two quantities can be readily determined. The relationships are shown graphically in Figure 1.
Example 1
Equilibrium Constants, Standard Cell Potentials, and Standard Free Energy Changes
What is the equilibrium constant and standard free energy change for the following reaction at 25 °C?
[latex]2\text{Ag}^{+}(aq)\;+\;\text{Fe}(s)\;{\rightleftharpoons}\;2\text{Ag}(s)\;+\;\text{Fe}^{2+}(aq)[/latex]
SOLUTION
The reaction involves an oxidation-reduction reaction, so the standard cell potential can be calculated using the table of reduction potentials (Source: OpenStax Chemistry 2e).
\begin{align*} &\text{anode (oxidation):} & \text{Fe}(s) &\longrightarrow \text{Fe}^{2+}(aq)\;+\;2\text{e}^{-} && E_{\text{Fe}^{2+}/\text{Fe}}^{\circ} = -0.447\;\text{V} \\[0.5em] &\text{cathode (reduction):} & 2\;\times\;\{\text{Ag}^{+}(aq)\;+\;\text{e}^{-} &\longrightarrow \text{Ag}(s)\} && E_{\text{Ag}^{+}/\text{Ag}}^{\circ} = +0.7996\;\text{V}\end{align*}
[latex]\begin{eqnarray} E_{\text{cell}}^{\circ} &=& E_{\text{cathode}}^{\circ}\;-\;E_{\text{anode}}^{\circ} \\ &=& E_{\text{Ag}^{+}/\text{Ag}}^{\circ}\;-\;E_{\text{Fe}^{2+}/\text{Fe}}^{\circ} \\ &=& +1.247\;\text{V} \end{eqnarray}[/latex]
Remember that the cell potential for the cathode is not multiplied by two when determining the standard cell potential. With n = 2 electrons, the equilibrium constant is then
[latex]\begin{eqnarray} E_{\text{cell}}^{\circ} &=& \frac{0.0592\;\text{V}}{n}\;\text{log}\;K \\[1 em] K &=& 10^{n\;\times\;E_{\text{cell}}^{\circ}/0.0592\;\text{V}} \\ &=& 10^{2\;\times\;1.247\;\text{V}/0.0592\;\text{V}} \\&=& 10^{42.1} \\ &=& \boxed{1\;\times\;10^{42}} \end{eqnarray}[/latex]
The molar change in standard free energy is then
[latex]\begin{eqnarray} {\Delta}G_{\text{r}}^{\circ} &=& -nFE_{\text{cell}}^{\circ} \\ &=& -2\;\times\;96485\;\frac{\text{J}}{\text{mol}{\cdot}\text{V}}\;\times\;1.247\;\text{V} \\ &=& \boxed{-240.6\;\frac{\text{kJ}}{\text{mol}}} \end{eqnarray}[/latex]
A positive standard cell potential means a spontaneous reaction, so the standard free energy change should be negative, and an equilibrium constant should be >1.
The Nernst Equation
Now that the connection has been made between the free energy and cell potentials, nonstandard concentrations follow. Recall from Section 5.6 that
[latex]{\Delta}G_{\text{r}} = {\Delta}G_{\text{r}}^{\circ}\;+\;RT\;\text{ln}\;Q[/latex]
where Q is the reaction quotient. Converting to cell potentials
[latex]-nFE_{\text{cell}} = -nFE_{\text{cell}}^{\circ}\;+\;RT\;\text{ln}\;Q[/latex]
Equation 5
[latex]E_{\text{cell}} = E_{\text{cell}}^{\circ}\;-\;\frac{RT}{nF}\;\text{ln}\;Q[/latex]
- [latex]E_{\text{cell}}[/latex], cell potential ([latex]\text{V}[/latex]); [latex]^\circ[/latex] denotes standard condition
- [latex]R[/latex], gas constant ([latex]8.314\;\frac{\text{J}}{\text{mol}{\cdot}\text{K}}[/latex])
- [latex]T[/latex], kelvin or absolute temperature
- [latex]n[/latex], number of electrons transferred in the balanced equation (unitless)
- [latex]F[/latex], Faraday’s constant ([latex]96485\;\frac{\text{J}}{\text{mol}{\cdot}\text{V}}[/latex])
- [latex]Q[/latex], reaction quotient
This is the Nernst equation for computing nonstandard cell potentials. At 298.15 K, it is possible to write the above equations as
Equation 6
[latex]E_{\text{cell}} = E_{\text{cell}}^{\circ}\;-\;\frac{0.0257\;\text{V}}{n}\;\text{ln}\;Q\;\;\;\;\;\;\;\text{or}\;\;\;\;\;\;\;E_{\text{cell}} = E_{\text{cell}}^{\circ}\;-\;\frac{0.0592\;\text{V}}{n}\;\text{log}\;Q[/latex] (at 298.15 K)
- [latex]E_{\text{cell}}[/latex], cell potential ([latex]\text{V}[/latex]); [latex]^\circ[/latex] denotes standard condition
- [latex]n[/latex], number of electrons transferred in the balanced equation (unitless)
- [latex]Q[/latex], reaction quotient
![]()
If the temperature is not 298.15 K, it is necessary to use Equation 5 and input the appropriate temperature.
Example 2
Cell Potentials at Nonstandard Conditions
Consider the following reaction at room temperature (298.15 K)
[latex]\text{Co}(s)\;+\;\text{Fe}^{2+}(aq\text{, }1.94\;\text{M})\;{\longrightarrow}\;\text{Co}^{2+}(aq\text{, }0.15\;\text{M})\;+\;\text{Fe}(s)[/latex]
Is the process spontaneous?
SOLUTION
There are two ways to solve the problem. If the thermodynamic information (Source: OpenStax Chemistry 2e) were available, you could calculate the free energy change. If the free energy change is negative, the process is spontaneous. The other approach, which we will use, requires standard reduction potentials (Source: OpenStax Chemistry 2e). Using those data, the cell potential can be determined. If the cell potential is positive, the process is spontaneous. Collecting information from the table of standard reduction potentials and the problem,
[latex]\begin{align*}&\text{anode (oxidation):} & \text{Co}(s) &\longrightarrow \text{Co}^{2+}(aq)\;+\;2\text{e}^{-} && E_{\text{Co}^{2+}/\text{Co}}^{\circ} = -0.28\;\text{V} \\[0.5em] &\text{cathode (reduction):} & \text{Fe}^{2+}(aq)\;+\;2\text{e}^{-} &\longrightarrow \text{Fe}(s) && E_{\text{Fe}^{2+}/\text{Fe}}^{\circ} = -0.447\;\text{V} \end{align*}[/latex]
[latex]\begin{eqnarray} E_{\text{cell}}^{\circ} &=& E_{\text{cathode}}^{\circ}\;-\;E_{\text{anode}}^{\circ} \\ &=& -0.447\;\text{V}\;-\;(-0.28\;\text{V}) \\ &=& -0.17\;\text{V} \end{eqnarray}[/latex]
The process is not spontaneous under standard conditions. Using the Nernst equation and the concentrations stated in the problem and n = 2 electrons
[latex]Q = \frac{[\text{Co}^{2+}]}{[\text{Fe}^{2+}]} = \frac{0.15}{1.94} = 0.077[/latex]
[latex]\begin{eqnarray} E_{\text{cell}} &=& E_{\text{cell}}^{\circ}\;-\;\frac{0.0592\;\text{V}}{n}\;\text{log}\;Q \\ &=& -0.17\;\text{V}\;-\;\frac{0.0592\;\text{V}}{2}\;\text{log}\;0.077 \\ &=& -0.17\;\text{V}\;+\;0.033\;\text{V} \\ &=& -0.014\;\text{V} \end{eqnarray}[/latex]
The process is (still) nonspontaneous.
We will take a brief look at a special type of cell called a concentration cell. In a concentration cell, the electrodes are the same material and the half-cells differ only in concentration. Since one or both compartments are not standard, the cell potentials will be unequal; therefore, there will be a potential difference, which can be determined with the aid of the Nernst equation.
The reason a concentration cell shows a positive cell potential is that we have the different solution concentrations of the same chemical in each of the half-cells. If we were to physically mix the more concentrated and less concentrated solutions in the same container, we would see spontaneous mixing as the universe strives to create a single uniform concentration in the single container. Therefore, a concentration cell is an electrochemical way of performing “mixing to uniform concentration”. The high concentration solution will see metal ions removed from solution as reduction takes place at the cathode and the high concentration will continually decrease, while the low concentration solution will see metal ions added as oxidation occurs at the anode, and the low concentration will continuously increase. As the solution concentrations get closer to each other, the positive cell potential will decrease to lower positive values until the concentrations in both half-cells are the same. At this point the two solutions are of identical concentration, equilibrium has been achieved, and the cell potential will have become zero. The “mixing” is done!
Example 3
Concentration Cells
What is the cell potential of the concentration cell described by
[latex]\text{Zn}(s){\mid}\text{Zn}^{2+}(aq\text{, }0.10\;\text{M}){\parallel}\text{Zn}^{2+}(aq\text{, }0.50\;\text{M}){\mid}\text{Zn}(s)[/latex]
SOLUTION
From the information given
[latex]\begin{align*} &\text{anode:} & \text{Zn}(s) &\longrightarrow \text{Zn}^{2+}(aq\text{, }0.10\;\text{M})\;+\;2\text{e}^{-} && E_{\text{anode}}^{\circ} = -0.7618\;\text{V} \\[0.5em] &\text{cathode:} & \text{Zn}^{2+}(aq\text{, }0.50\;\text{M})\;+\;2\text{e}^{-} &\longrightarrow \text{Zn}(s) && E_{\text{cathode}}^{\circ} = -0.7618\;\text{V} \\[0.5em] \hline &\text{overall:} & \text{Zn}^{2+}(aq\text{, }0.50\;\text{M}) &\longrightarrow \text{Zn}^{2+}(aq\text{, }0.10\;\text{M}) && E_{\text{cell}}^{\circ} = 0.000\;\text{V} \end{align*}[/latex]
The standard cell potential is zero because the anode and cathode involve the same reaction; only the concentration of Zn2+ changes. Substituting into the Nernst equation
[latex]E_{\text{cell}} = 0.000\;\text{V}\;-\;\frac{0.0592\;\text{V}}{2}\;\text{log}\;\frac{0.10}{0.50} = +0.021\;\text{V}[/latex]
and the process is spontaneous at these conditions.
In a concentration cell, the standard cell potential will always be zero. To get a positive cell potential (spontaneous process) the reaction quotient Q must be <1 as is the case here, so the process is spontaneous.
We can even extend electrochemical calculations for solving reactions that are not redox, such as acid ionization (Example 4) and solubility (Example 5). The trick is to couple two reduction-oxidation half-reactions to reconstruct the non-redox reaction of interest.
Example 4
Calculating the Ionization Constant of an Acid
What is the ionization constant of hydrofluoric acid at 298.15 K, given the following half-reactions
[latex]\begin{align*} \text{F}_2(g)+2\text{H}^+(aq)+2\text{e}^{-} &\longrightarrow 2\text{HF}(aq) && E^{\circ} = +3.05\;\text{V}\\[0.5em] \text{F}_2(g)+2\text{e}^{-} &\longrightarrow 2\text{F}^-(aq) && E^{\circ} = +2.87\;\text{V} \end{align*}[/latex]
Standard reduction potentials from Bard AJ, Parsons R, Jordan J (1985) Standard Potentials in Aqueous Solution. CRC Press.
SOLUTION
From the information given
[latex]\begin{align*} &\text{anode:} & 2\text{HF}(aq) &\longrightarrow \text{F}_2(g)+2\text{H}^+(aq)+2\text{e}^{-} && E_{\text{anode}}^{\circ} = +3.05\;\text{V} \\[0.5em] &\text{cathode:} & \text{F}_2(g)+2\text{e}^{-} &\longrightarrow 2\text{F}^-(aq) && E_{\text{cathode}}^{\circ} = +2.87\;\text{V} \\[0.5em] \hline &\text{overall:} & 2\text{HF}(aq)+\text{F}_2(g) & \longrightarrow \text{F}_2(g)+2\text{H}^+(aq)+2\text{F}^-(aq)&& E_{\text{cathode}}^{\circ} = -0.18 \text{ V}\end{align*}[/latex]
Arrange the equation into the form for acid ionization. We can multiply the reaction by ½ without affecting the cell potential. In electrochemistry, we use “H+” as an abbreviation of “H3O+” from the acid-base unit.
[latex]\begin{align*} 2\text{HF}(aq) &\longrightarrow 2\text{H}^+(aq)+2\text{F}^-(aq) \\ \text{HF}(aq) &\longrightarrow \text{H}^+(aq)+\text{F}^-(aq) \end{align*}[/latex]
In multiplying the reaction by ½, we also halve the number of electrons transferred in the reaction. Instead of 2 e−, the modified reaction now exchanges n = 1 e−.
[latex]\begin{array}{l r l} & E^{\circ}_{\text{cell}}&=\frac{0.0592\text{ V}}{n}\log K_{\text{a}}\\ \Leftrightarrow &\log K_{\text{a}} &= \frac{nE^{\circ}_{\text{cell}}}{0.0592 \text{ V}} \\ &&=\frac{(1)(-0.18 \text{ V})}{0.0592 \text{ V}} \\ &&= -3.0\end{array}[/latex]
Calculate Ka
[latex]\begin{array}{r l} K_{\text{a}}&=10^{\log K_{\text{a}}} \\ &=10^{-3.0} \\ &= \boxed{9\times 10^{-4}}\end{array}[/latex]
Example 5
Calculating the Solubility Product Constant
What is the solubility product constant of zinc sulfide at 298.15 K, given the following half-reactions
[latex]\begin{align*} \text{ZnS}(s)+2\text{e}^{-} &\longrightarrow \text{Zn}(s)+\text{S}^{2-}(aq) && E^{\circ} = -1.40\;\text{V} \\[0.5em] \text{Zn}^{2+}(aq)+2\text{e}^{-} &\longrightarrow \text{Zn}(s) && E^{\circ} = -0.7618\;\text{V}\end{align*}[/latex]
SOLUTION
From the information given
[latex]\begin{align*} &\text{anode:} & \text{Zn}(s) &\longrightarrow \text{Zn}^{2+}(aq)+2\text{e}^{-} && E_{\text{anode}}^{\circ} = -0.7618\;\text{V} \\[0.5em] &\text{cathode:} & \text{ZnS}(s)+2\text{e}^{-} &\longrightarrow \text{Zn}(s)+\text{S}^{2-}(aq) && E_{\text{cathode}}^{\circ} = -1.40\;\text{V} \\[0.5em] \hline &\text{overall:} & \text{ZnS}(s)+\text{Zn}(s) &\longrightarrow \text{Zn}(s)+\text{Zn}^{2+}(aq)+\text{S}^{2-}(aq) && E_{\text{cell}}^{\circ}= -0.64 \text{ V} \end{align*}[/latex]
Arrange the equation into the form for dissolution
[latex]\text{ZnS}(s) \longrightarrow \text{Zn}^{2+}(aq)+\text{S}^{2-}(aq)[/latex]
Calculate Ksp
[latex]\begin{array}{l r l} & E^{\circ}_{\text{cell}}&=\frac{0.0592\text{ V}}{n}\log K_{\text{sp}}\\ \Leftrightarrow &\log K_{\text{sp}} &= \frac{nE^{\circ}_{\text{cell}}}{0.0592 \text{ V}} \\ &&=\frac{(2)(-0.64 \text{ V})}{0.0592 \text{ V}} \\ &&= -2.2\times10^1\end{array}[/latex]
[latex]\begin{align*} K_\text{sp}&=10^{\log K_\text{sp}} \\ &=10^{-2.2\times10^1} \\ &=\boxed{3\times10^{-22}} \end{align*}[/latex]
Data Table
Standard reduction potentials for select substances (Source: OpenStax Chemistry 2e). The table is listed in alphabetical order of the chemical symbol and not in order of the reduction potentials.
Optional Resource
Watch a video example of using the Nernst equation.
Video 1 Nernst Equation Example (5 min 30 s).
Given the standard reduction potentials (Source: OpenStax Chemistry 2e)Au+(aq) + e– → Au(s) E° = +1.69 V
Ag+(aq) + e– → Ag(s) E° = +0.80 Vfind the change in Gibbs energy for the reaction at 298 K
Au+(aq) + Ag(s) → Au(s) + Ag+(aq)
when [Au+(aq)] = 0.257 M and [Ag+(aq)] = 0.555 M.
Click to see answer
[latex]Q=\frac{[\text{Ag}^+]}{[\text{Au}^+]} = \frac{0.555}{0.257} \\ \\ E = E^\circ – \frac{RT}{nF} \ln Q \\ = (+1.69 \text{ V} – (+0.80 \text{ V})) – \frac{(8.314 \text{ J mol}^{–1} \text{ K}^{–1}) (298 \text{ K})}{(1)(96485 \text{ J mol}^{–1} \text{ V}^{–1})}\ln\frac{0.555}{0.257}\\ = 0.87 \text{ V} \\ \\ \Delta G = –nFE \\ = –(1 \text{ mol})\left(96485 \text{ J mol}^{–1} \text{ V}^{–1}\right)(0.87 \text{ V}) \\ = \boxed{–84.0 \text{ kJ}}[/latex]
✩ UNIT 6 ASSIGNMENT
Complete Unit 6 Assignment (graded) on Moodle. This assignment is worth 11% of the course grade.

